Слайд 2
Factorial: trace
A subroutine is said to be recursive
if it calls itself, either directly or indirectly. That
is, the subroutine is used in its own definition.
fact(3)
==> 3 * fact(3 - 1)
==> 3 * fact(2)
==> 3 * (2 * fact(2 - 1))
==> 3 * (2 * fact(1))
==> 3 * (2 * (1 * fact(1 - 1)))
==> 3 * (2 * (1 * fact(0)))
==> 3 * (2 * (1 * 1))
==> 6
Слайд 3
Recursive objects in the world. Fractal objects
A huge
amount of of things in the real world has
a recursive nature.
For example, coastline of a sea has a fractal nature – fractals are recursive: their structure is repeated over and over in small details. i.e it is a rough or fragmented geometric shape that can be subdivided in parts, each of which is (at least approximately) a reduced-size copy of the whole
Sierpinski triangle:
Слайд 4
Recursion
A subroutine is said to be recursive if
it calls itself, either directly or indirectly. That is,
the subroutine is used in its own definition.
Bad kind - infinite loop:
a car is a car,
int fact(int x) {
return fact(x)
}
Recursion can often be used to solve complex problems by reducing them to simpler problems of the same type.
Good kind – loop is (hopefully) terminated:
An "ancestor" is either a parent or an ancestor of a parent.
int fact (int x) {
if (x <= 0) return 1;
else return x * fact(x-1);
}
Слайд 5
Recursive functions: main principles
Important to check that
recursion terminates. Code should contain:
One or more base cases
(no recursion involved!)
One or more recursive cases. Arguments of the recursive call must be “simpler” according to some measure.
NB! The “simplicity” measure may be arbitrarily complex.
Слайд 6
Recursive functions: main principles
Recursion has same power
as iteration:
Every recursive function can be written using while
or for loops instead
Every function using while and/or for loops can be written using recursion instead
However:
some programming tasks are much easier to write using recursion
some programming tasks are much easier to write using iteration
Слайд 7
Direct and indirect recursive call
A recursive subroutine
is one that calls itself, either directly or indirectly.
To say that a subroutine calls itself directly means that its definition contains a subroutine call statement that calls the subroutine that is being defined.
foo calls foo:
int foo(int x) { if (x>0) return 1+foo(x-1) else return 1}
To say that a subroutine calls itself indirectly means that it calls a second subroutine which in turn calls the first subroutine (either directly or indirectly).
foo calls bar which calls foo:
int foo(int x) { if (x>0) return 2+bar(x-2) else return 1}
int bar(int x) { if (x>0) return 2*+foo(x-1) else return 1}
Слайд 8
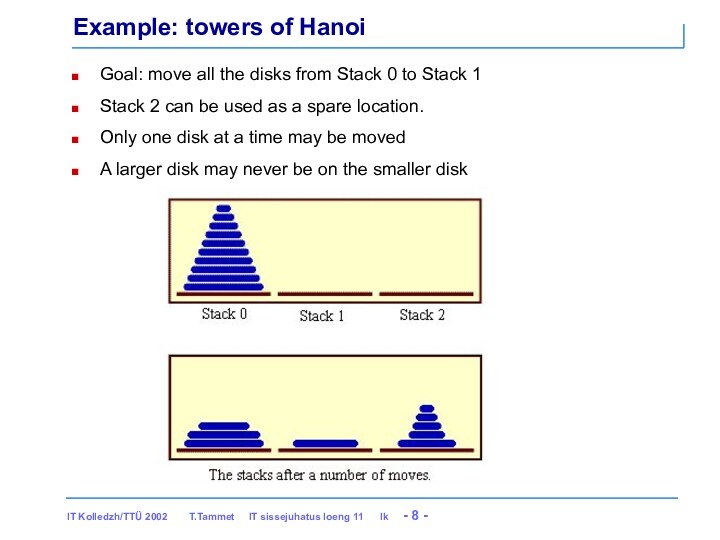
Example: towers of Hanoi
Goal: move all the disks
from Stack 0 to Stack 1
Stack 2 can be
used as a spare location.
Only one disk at a time may be moved
A larger disk may never be on the smaller disk
Слайд 9
towers of Hanoi
Move two elements
So we have an
algorithm to move two elements
Слайд 10
towers of Hanoi
Move three elements
Use al algorithm to
move two elements: notice evrywhere either a base or
a bigger element
Move the biggest
Use al algorithm to move two elements: notice everywhere again either a base or a bigger element
So we have an algorithm to move three elements
Слайд 11
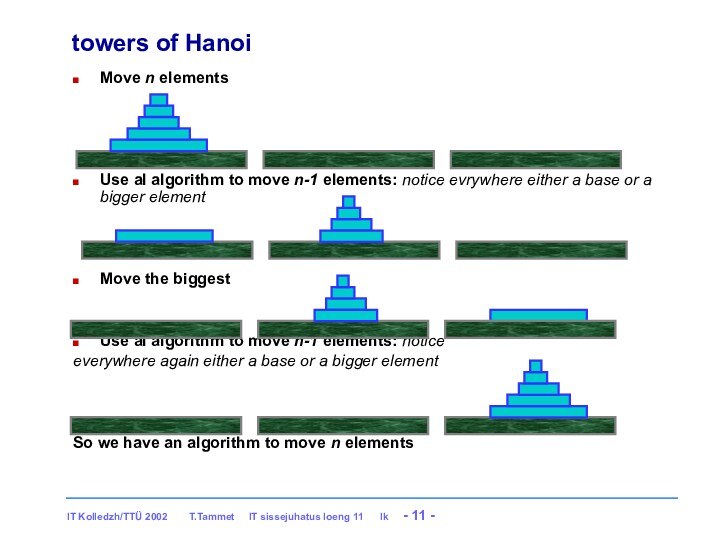
towers of Hanoi
Move n elements
Use al algorithm to
move n-1 elements: notice evrywhere either a base or
a bigger element
Move the biggest
Use al algorithm to move n-1 elements: notice
everywhere again either a base or a bigger element
So we have an algorithm to move n elements
Слайд 12
Recursive binary search
static int binarySearch(int[] A, int loIndex,
int hiIndex, int value) {
if (loIndex > hiIndex) {
return -1;
}
else {
int middle = (loIndex + hiIndex) / 2;
if (value == A[middle])
return middle;
else if (value < A[middle])
return binarySearch(A, loIndex, middle - 1, value);
else // value must be > A[middle]
return binarySearch(A, middle + 1, hiIndex, value);
}
} // end binarySearch()
Слайд 13
Binary search
Look for 15
1, 2, 5, 8, 13,
15, 23, 25, 45
1, 2, 5, 8, 13, 15,
23, 25, 45: index: [lowindex(1)+highindex(9)]/2=10/2=5
15>13: start binary_search(search:15, lowindex: 6 [5+1], higindex: 9)
1, 2, 5, 8, 13, 15, 23, 25, 45: index: [lowindex(6)+highindex(9)]/2=15/2=7.5=>7
15<23: start binary_search(search:15, lowindex: 6, highindex: 6 [7-1])
1, 2, 5, 8, 13, 15, 23, 25, 45: index: [lowindex(6)+highindex(6)]/2=12/2=6
The element is found in 3 steps
Слайд 14
Deklaratiivne vs imperatiivne
Programmeerimiskeeli ja -meetodeid saab klassifitseerida
mitmel moel. Selle loengu kontekstis sobib jaotada programmeerimiskeeled kõigepealt
kahte gruppi:
Imperatiivsed keeled - sobivad samm-sammult, kindlas järjekorras täidetavate algoritmide esitamiseks. Programmid kujutavad endast arvutile antavate käskude jada. Tuntumad imperatiivsed keeled on C, Basic, Pascal, Java, objektorienteeritud keeled ja assemblerkeeled.
Procedural programmingprogramming is imperative programming in which the program is built from one or more procedures (also known as subroutines or functions).
Imperatiivsete keelte peamiseks eeliseks on arvuti tegevuse täpse kontrollimise ja suunamise võimaldamine, mis enamasti tagab maksimaalse töökiiruse.
Miinusteks on programmeerimise suur töömahukus - lahenduskäigu kõik detailid tuleb süsteemile esitada - ning suured raskused programmideanalüüsimisel, näiteks optimeerimise, verifitseerimise või paralleliseerimise tarvis.
Слайд 15
Deklaratiivsed vs imperatiivsed keeled
Deklaratiivsed keeled sobivad algoritmi esitamiseks
käskude jadast abstraktsemal viisil. Programmeerija ei pruugi alati kõiki
algoritmi detaile kirja panna, vaid võib esitada otsitava lahenduse kirjelduse , ning juba programmi täitmise käigus otsustab süsteem automaatselt, mis viisil täpselt seda lahendust otsida.
Deklaratiivseteks keelteks võib lugeda loogilise programmeerimise keeled (näiteks Prolog) ja mitmed funktsionaalsed keeled (näiteks Haskell). Teoorias kasutatav lambda-arvutus on puhtalt funktsionaalse deklaratiivse keele näide.
Common declarative languages include those of database query languagesCommon declarative languages include those of database query languages (e.g., SQLCommon declarative languages include those of database query languages (e.g., SQL, XQueryCommon declarative languages include those of database query languages (e.g., SQL, XQuery), regular expressions, and mentioned above
Слайд 16
Plussid ja miinused
Deklaratiivsed keeled võimaldavad enamikku programme kiiremini
ja mugavamalt kirjutada, kui imperatiivsed keeled - programmeerija ei
pea kõigi detailide eest hoolt kandma. Tunduvalt lihtsam on ka programmide analüüs, näiteks programmi automaatsel kohandamisel paralleelarvutile, kus programmi täitmise juures töötab samaaegselt hulk protsessoreid.
Peamiseks miinuseks on programmide väiksem töökiirus - deklaratiivne programm ei pruugi küll alati aeglasem olla, kui imperatiivne, kuid on seda harilikult siiski. Põhjuseks on siin keele automaattranslaatori väiksem intelligentsus kogenud programmeerijaga võrreldes.
Слайд 17
Funktsionaalsed ja loogilised keeled
Deklaratiivsed keeled jaotatakse
Funktsionaalse
programmeerimise keelteks (näide: Haskell), kus lahendus kirjeldatakse funktsioonide kogu
abil - ka viimast saab tegelikult käsitleda kui teatud tüüpi loogikasüsteemi.
Loogilise programmeerimise keelteks (näide: Prolog), kus otsitavat lahendust kirjeldatakse loogika keeles
Слайд 18
Alus: lambda-arvutus
Lambda-arvutuse keel on Alonzo Churchi poolt 1930.
aastatel leiutatud lihtne ja universaalne meetod funktsioonide kirjapanekuks.
Lambda-arvutuse
teooria tegeleb arvutatavuse ja arvutatavate funktsioonide uurimisega, kasutades selleks lambda-arvutuse keelt kui universaalset programmeerimiskeelt.
Churchi tees väidab, et iga algoritmi saab lambda-arvutuse keeles kirja panna. On võimalik näidata, et lambda-arvutus, nagu ka Prolog, C ja Basic on üks paljudest universaalsetest programmeerimiskeeltest.
Konkreetselt on lambda-arvutuse keel ja teooria funktsionaalsete programmeerimiskeelte aluseks.
Слайд 19
Annonüümsed funktsioonid
üks harilikumaid praktikas kasutatavaid funktsioonide kirjapaneku viise
on selline:
f(x) = x*x + 1
Funktsioon esitatakse, andes talle
samas nime, konkreetses näites f. Lambda-arvutuses esitatakse funktsioone, vastupidi, kui anonüümseid, nimeta terme. äsjatoodud näide on lambda-kirjaviisis
λ x. x*x + 1
Lambda-sümboli λ järele kirjutatakse funktsiooni formaalseks parameetriks olev muutuja, seejärel punkt ja funktsiooni keha.









![Sissejuhatus informaatikasse. 11. Loeng Recursive binary searchstatic int binarySearch(int[] A, int loIndex, int hiIndex, int](/img/tmb/14/1397384/c7672a277f0455bf3fb86dabf87b2336-720x.jpg)