- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Системы счисления
Содержание
- 2. Системой счисления называется способ записи (кодирования) чисел.
- 3. Позиционной называется такая система счисления, в которой
- 4. Пример: арабская система счисления, которой мы обычно
- 5. Если же величина цифры не зависит от
- 6. Непозиционные системы счисления первичны по своему происхождению;
- 7. Алфавит Римской системы I V
- 8. Числа в римской системе счисления записываются по
- 9. 2) если меньшая цифра стоит перед большей,
- 10. Например число 1996 будет записано в римской система счисления как MCMXCVI.
- 11. Самое большое число, которое можно записать в
- 12. А теперь попробуйте выполнить простую арифметическую операцию,
- 13. Недостатки непозиционных систем счисления: а)
- 14. Вопросы и упражнения.1. Что такое система
- 15. Вопросы и упражнения.5. Почему двоичная система
- 17. Числа в разных системах счисления:
- 18. Семакин стр.36-38
- 19. Перевод из десятичной системы в двоичнуюПринцип: делить
- 20. Что больше 1 или 9? (Понятно что
- 21. 10000 1000 100
- 22. Можно рассматривать системы счисления и с другими
- 23. Перевод чисел в десятичную СС из других
- 24. Показать принцип на примерах
- 25. пример: переведем число 542 из 8-ричной в
- 26. Еще примеры: 3В916 = 3*16 2
- 27. Скачать презентацию
- 28. Похожие презентации
Системой счисления называется способ записи (кодирования) чисел. Все системы счисления можно разделить на две группы: позиционные и непозиционные.















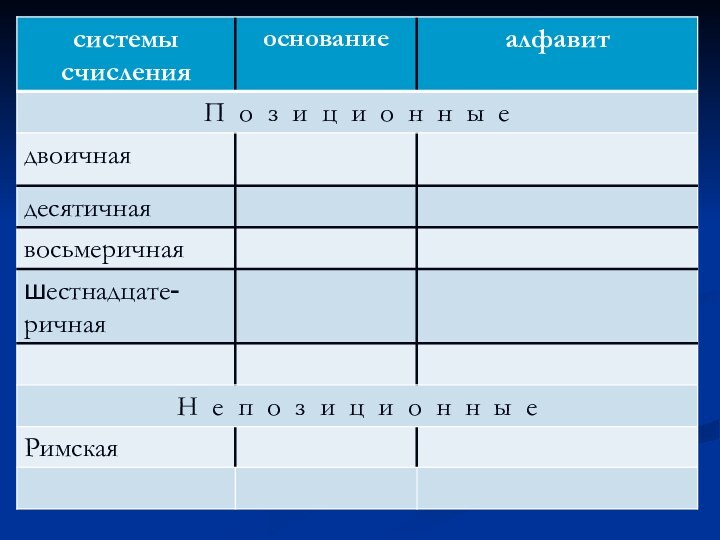











Слайд 3 Позиционной называется такая система счисления, в которой величина
цифры зависит от позиции (места), занимаемой этой цифрой в
записи числа.Слайд 4 Пример: арабская система счисления, которой мы обычно пользуемся.
Если взять два числа 102 и 21, то цифра
1 в первом числе в 100 раз "тяжелее" той же цифры во втором числе. А вот цифра 2 в первом числе в 10 раз "легче" этой же цифры во втором числе.Слайд 5 Если же величина цифры не зависит от места,
занимаемого этой цифрой, то такая система счисления называется непозиционной.
Слайд 6 Непозиционные системы счисления первичны по своему происхождению; но
поскольку они имеют ряд недостатков по сравнению с позиционными
системами счисления, то постепенно они потеряли свое значение.Слайд 8 Числа в римской системе счисления записываются по определенным
правилам:
1) если большая цифра стоит
перед меньшей, они складываются, например: VI=6;
Слайд 9 2) если меньшая цифра стоит перед большей, то
из большей вычитается меньшая, причем в этом случае меньшая
цифра уже повторяться не может,например: XL=40, XXL-нельзя;
3) цифры M,C,X,I могут повторяться в записи числа не более трех раз подряд;
4) цифры D,L,V могут использоваться в записи числа только по одному разу.
Слайд 11 Самое большое число, которое можно записать в этой
системе счисления, это число 3999 MMMCMXCIX.
Для записи еще
больших чисел пришлось бы вводить еще новые обозначения.Слайд 12 А теперь попробуйте выполнить простую арифметическую операцию, не
переводя числа в привычную систему счисления:
умножить
число CLVI на число LXXIV. Вряд ли вам это удастся.
Слайд 13
Недостатки непозиционных систем счисления:
а) нельзя
записывать сколь угодно большие числа;
б) запись
чисел обычно громоздка и неудобна;в) математические операции над числами крайне затруднены.
Именно поэтому, хотя римская и очень "красивая" система счисления, она не получила широкого распространения.
Слайд 14
Вопросы и упражнения.
1. Что такое система счисления
?
2. В чем отличие позиционной системы счисления от непозиционной
?3. Во сколько раз цифра 5 "тяжелее" в первом числе по сравнению с этой же цифрой второго числа:
15243 и 750 ?
4. Во сколько раз первая цифра 3, встречающаяся в числе "тяжелее" второй такой же цифры
а) 33765 ; б) 37653 ?
Слайд 15
Вопросы и упражнения.
5. Почему двоичная система счисления
получила широкое распространение?
6. Почему непозиционные системы счисления потеряли
свое значение ?7. Приведите примеры, где римские цифры используются в наше время.
8. Перемножьте числа 23 и 17. Запишите все три числа в римской системе счисления.
Слайд 19
Перевод из десятичной системы в двоичную
Принцип: делить число
на 2 и собирать остатки от деления в обратном
порядке.Показать на примерах
Слайд 20 Что больше 1 или 9? (Понятно что 9).
Но в числе 13509 важнее играет роль 1. И
это всем понятно так как мы привыкли с начальной школы читать это число следующим образом: начиная слева цифру умножаем на соответствующий разряд в котором она находится складываем со следующей цифрой, умноженной на свой соответствующий разряд и т.л., пока не дойдем до последней цифры.
Слайд 21
10000 1000 100 10
1 - разряды
1
3 5 0 9 = = 1*10000 + 3*1000 + 5*100 + 9*1 =
= 1*10 4+ 3*10 3 + 5*10 1 + 9*10 0
Слайд 22 Можно рассматривать системы счисления и с другими основаниями.
Если р - основание системы счисления, то любое число
N в этой системе счисления может быть представлено в видеN =а(n)*р^n + a(n-1)*p^(n-1) + ... + a(1)*p + a(0), где коэффициенты - цифры р-ичной системы счисления.
Слайд 23 Перевод чисел в десятичную СС из других СС
осуществляется с помощью записи их в виде суммы степеней
основания :N =а(n)*рn + a(n-1)*p(n-1) + ... + a(1)*p + a(0),
где р - основание системы счисления, коэффициенты - цифры р-ичной системы счисления.
Слайд 25 пример: переведем число 542 из 8-ричной в десятичную
СС.
Для этого представим число 542 в виде суммы
степеней основания 8:5428 = 5*8 2 + 4*8 1 + 2*8 0 .
Теперь произведем вычисления:
5*8 2 + 4*8 1 + 2*8 0 = 5*64 + 4*8 +2*1= 320 + 32 +2 = 35410.
Таким образом, 5428 = 35410.
Слайд 26
Еще примеры:
3В916 = 3*16 2 +
11*16 1 + 9*16 0 =
=3*256 +
11*16 + 9*1 = 95310.110101 = 1*2 5 + 1*2 4 + 0*2 3 + 1*2 2 +1*0 1 + 1*2 0 =
=32 + 16 + 0 + 4 + 0 +1 = 5310.