- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сложность алгоритмов
Содержание
- 2. План:1. Временная сложность алгоритма2. Асимптотическая сложность3. Классы сложности алгоритмов
- 3. Центральная задача теории алгоритмов —
- 4. 1. Временная сложность алгоритма
- 5. Исполнение любого алгоритма требует: определенного объема памяти
- 6. Эффективным называется алгоритм, обеспечивающий наиболее
- 7. Временная сложность – быстродействие
- 8. Время работы алгоритма (Т) -
- 9. Временная сложность алгоритма Т(n)- это
- 10. Пример математической оценки временной сложности алгоритмаРассмотрим два
- 11. Алгоритм 2:вынесем Х-ы за скобки и перепишем
- 12. В теоретической информатике при сравнении
- 13. Функция T(n) = n2/2 +
- 15. Правила формирования оценки O ()1. При определении
- 16. 2. При оценке O() константы не учитываютсяСледствия:1)
- 17. 2) Алгоритм со временем O(n2) может работать
- 18. 3) Основание логарифма внутри символа O() не
- 19. 3. Классы сложности алгоритмов
- 20. Множество вычислительных проблем, для которых
- 21. Класс сложности: О(1)Название: Алгоритмы единичной сложностиХарактеристика:
- 22. Класс сложности: О(log n)Название: Алгоритмы логарифмической сложностиПример: большинство алгоритмов поиска
- 23. Пример алгоритма сложности О(log n) Двоичный поиск
- 24. T(n) = log2n + 1.
- 25. Класс сложности: О(n)Название: Алгоритмы линейной сложностиХарактеристика:
- 26. Пример алгоритма сложности О(n) Линейный поиск
- 27. В этом алгоритме число сравнений (в худшем
- 28. Класс сложности: О(n* log n)Название: специального названия
- 29. Класс сложности: О(n2)Название: Алгоритмы квадратичной сложностиХарактеристика:
- 30. Сортировка обменом (метод пузырька)1. При 1м проходе
- 31. 7. Количество проходов по массиву равно m-1,
- 33. Для преобразования массива, состоящего из n элементов,
- 34. Сортировка выбором1. Найти максимальный элемент (max) в
- 36. Максимальное количество перестановок на некотором массиве длины
- 37. Класс сложности: О(n3)Название: Алгоритмы кубический сложностиХарактеристика:
- 38. Класс сложности: О(nх)Название: Полиномиальные алгоритмыХарактеристика:
- 39. В рамках теории сложности любые
- 40. Класс сложности: О(хn) Класс - EXPTIMEНазвание: Экспоненциальные
- 41. Класс сложности: О(n!)Название: Факториальные алгоритмыПримеры:
- 42. Наряду с алгоритмически неразрешимыми задачами, существуют объективно
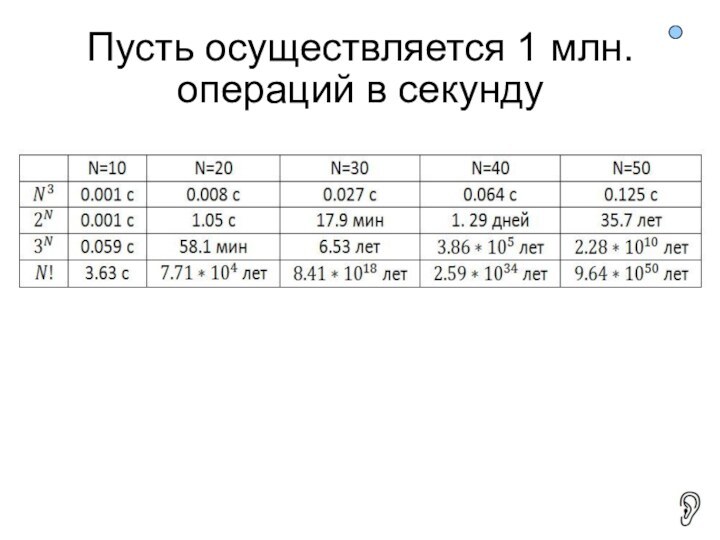
- 43. Пусть осуществляется 1 млн. операций в секунду
- 44. Вопросы к лекции1. Какой алгоритм называют эффективным?2.
- 45. Скачать презентацию
- 46. Похожие презентации
План:1. Временная сложность алгоритма2. Асимптотическая сложность3. Классы сложности алгоритмов













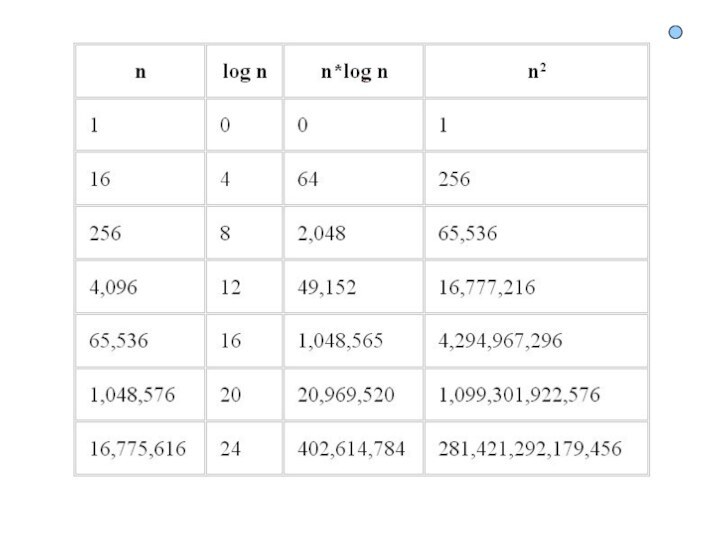






























Слайд 2
План:
1. Временная сложность алгоритма
2. Асимптотическая сложность
3. Классы сложности
алгоритмов
Слайд 3 Центральная задача теории алгоритмов — выяснить,
существует ли алгоритм решения той илииной задачи.
Если да, то можно ли им воспользоваться на практике, при современном уровне развития вычислительной техники? Т.е. способен ли компьютер за приемлемое время получить результат?
Слайд 5
Исполнение любого алгоритма требует:
определенного объема памяти компьютера
для размещения данных и программы,
времени процессора по обработке этих
данных.
Слайд 6
Эффективным называется алгоритм, обеспечивающий наиболее быстрое
получение результата в приемлемое время в ограниченном объеме оперативной
памяти.Для сравнения алгоритмов по эффективности необходимо уметь оценивать сложность алгоритмов
Слайд 7
Временная сложность – быстродействие
Пространственная
сложность – объем требуемой памяти
Для определения
сложности алгоритма оценивают временную сложность алгоритма
Слайд 8
Время работы алгоритма (Т) - количество
выполненных им элементарных операций (не в секундах!)
Позволяет оценивать именно качество алгоритма, а не свойства исполнителя (быстродействие компьютера)Размер задачи (n) - объем входных данных, необходимых для ее решения.
Слайд 9
Временная сложность алгоритма Т(n)- это функция,
которая каждому размеру задачи n ставит в соответствие максимальное
количество элементарных операций выполненных в ходе выполнения алгоритма
Слайд 10
Пример математической оценки временной сложности алгоритма
Рассмотрим два алгоритма
вычисления значения многочлена степени n в заданной точке x
Pn(x)
= anxn + an-1xn-1 + ... + aixi + ... + a1x1 + a0Алгоритм 1:
для каждого слагаемого, кроме a0 возвести x в заданную степень последовательным умножением и затем домножить на коэффициент. Затем слагаемые сложить.
Вычисление i-го слагаемого(i=1..n) требует i умножений.
Значит, всего 1 + 2 + 3 + ... + n = n(n+1)/2 умножений.
Кроме того, требуется n+1 сложение.
Всего n(n+1)/2 + n + 1= n2/2 + 3n/2 + 1 операций.
Слайд 11
Алгоритм 2:
вынесем Х-ы за скобки и перепишем многочлен
в виде
Pn(x) = a0 + x(a1 + x(a2 +
... ( ai + .. x(an-1 + anx))).Будем вычислять выражение изнутри.
Самая внутренняя скобка требует 1 умножение и 1 сложение.
Ее значение используется для следующей скобки...
И так, 1 умножение и 1 сложение на каждую скобку, которых.. n-1 штука.
И еще после вычисления самой внешней скобки умножить на x и прибавить a0.
Всего n умножений + n сложений = 2n операций.
Слайд 12
В теоретической информатике при сравнении алгоритмов
используется их асимптотическая сложность O() , т. е. скорость
роста количества операций при больших значениях n.Слайд 13 Функция T(n) = n2/2 + 3n/2
+ 1
возрастает приблизительно как n2
Отбрасываем:- сравнительно медленно растущие слагаемые (3n/2+1)
- константные множители 1/2
Получаем асимптотическую оценку сложности для алгоритма 1: O(n2) (О – нотация)
Читается как "О большое от эн квадрат".
Слайд 15
Правила формирования оценки O ()
1. При определении O()
берется наиболее быстро растущая часть T(n).
Например, если
в программе одна функция, например, умножение, выполняется O(n) раз, а сложение - O(n2) раз, то общая сложность программы - O(n2)
Слайд 16
2. При оценке O() константы не учитываются
Следствия:
1) Алгоритмы
с одинаковым O() могут иметь различную эффективность
Например,
один алгоритм делает 2n+1 операций, а другой - 2500n + 1000. Оба они имеют оценку O(n), так как их время выполнения растет линейно.
Слайд 17 2) Алгоритм со временем O(n2) может работать значительно
быстрее алгоритма O(n) при малых n.
Например, реальное
количество операций первого алгоритма может быть n2 + 10n + 6,а второго - 1000000*n + 5. (больше умножений)
Впрочем, второй алгоритм рано или поздно обгонит первый... n2 растет куда быстрее 1000000*n.
Слайд 18
3) Основание логарифма внутри символа O() не пишется
Например,
пусть у нас есть O(log2n),
но log2n=log3n/log32, а log32,
как и
любую константу, О() не учитывает.Таким образом, O(log2n) = O( log3n).
К любому основанию мы можем перейти аналогично, а значит и писать его не имеет смысла.
Слайд 20
Множество вычислительных проблем, для которых существуют
алгоритмы, схожие по временной сложности, называется классом сложности
Наиболее часто встречающиеся классы сложности :
Слайд 21
Класс сложности: О(1)
Название: Алгоритмы единичной сложности
Характеристика:
алгоритмы, использующие часть входных данных и игнорирующие все остальные
данные. Такие алгоритмы выполняется за один проход вне зависимости от значения nПример
Дан массив A длины n. Вычислить сумму первых трех элементов массива
Решение этой задачи содержит всего один оператор:
S := A[1] + A[2] + A[3], Т(n) = 3
Слайд 22
Класс сложности: О(log n)
Название: Алгоритмы логарифмической сложности
Пример: большинство
алгоритмов поиска
Слайд 23
Пример алгоритма сложности О(log n)
Двоичный поиск
Дан
массив, в котором элементы упорядочены по возрастанию.
Найти в нем
заданное значение x или сообщить,что его нет.
Применяется метод двоичного поиска (дихотомии): сначала ширина интервала поиска — все n элементовмассива. На каждом шаге этот интервал делится на 2, процесс завершается, когда левая и правая границы интервала совпадут.
Слайд 25
Класс сложности: О(n)
Название: Алгоритмы линейной сложности
Характеристика:
Для алгоритмов класса O(n) для каждого входного элемента выполняется
только одно действие.На самом деле, может быть, конечно, не одно, а два, три, и т.д., но главное не больше С*N, где С — константа.
Пример:
программы с конечным числом одномерных циклов, пробегающих весь набор входных данных, идущих друг за другом (вложенных циклов быть не может) + некоторый набор шагов до, после и между циклами. Просмотр обложки каждой поступающей книги - для каждого входного объекта выполняется только одно действие
Слайд 26
Пример алгоритма сложности О(n)
Линейный поиск
Дан массив,
в котором элементы расположены в произвольном порядке. Найти в
нем заданное значение x или сообщить, что его нет.Решение этой задачи сводится к последователь-
ному просмотру всех элементов массива
Слайд 27 В этом алгоритме число сравнений (в худшем случае)
равно T(n) = n, поэтому он имеет линейную сложность.
Слайд 28
Класс сложности: О(n* log n)
Название: специального названия не
имеет
Пример:
алгоритмы быстрой сортировки, сортировки слиянием и
"кучной" сортировки
Слайд 29
Класс сложности: О(n2)
Название: Алгоритмы квадратичной сложности
Характеристика:
Для алгоритмов класса O(n2) каждый входной элемент обрабатывается (или
проходится) С*n2 раз. Это означает (для наглядности, только как одну из возможностей) наличие вложенных (двойных) циклов.Пример:
в основном, все простейшие алгоритмы сортировки
Слайд 30
Сортировка обменом (метод пузырька)
1. При 1м проходе по
массиву элементы попарно сравниваются между собой: 1й со 2м,
затем 2й с 3м, следом 3й с 4м и т.д. Если предшествующий элемент оказывается больше последующего, то их меняют местами.2. Постепенно самое большое число оказывается последним. Остальная часть массива остается не отсортированной
3. При 2м проходе незачем сравнивать последний элемент с предпоследним. Последний элемент уже стоит на своем месте. Значит, число сравнений будет на одно меньше.
4. На 3м проходе уже не надо сравнивать предпоследний и 3й элемент с конца. Поэтому число сравнений будет на два меньше, чем при первом проходе.
5. В конце концов, при проходе по массиву, когда остаются только два элемента, которые надо сравнить, выполняется только одно сравнение.
6. После этого первый элемент не с чем сравнивать, и, следовательно, последний проход по массиву не нужен.
Слайд 31
7. Количество проходов по массиву равно m-1, где
m – это количество элементов массива.
8.Количество сравнений в каждом
проходе равно m-i, где i – это номер прохода по массиву (первый, второй, третий и т.д.).9. При обмене элементов массива обычно используется "буферная" (третья) переменная, куда временно помещается значение одного из элементов.
Слайд 33
Для преобразования массива, состоящего из n элементов, необходимо
просмотреть его n-1 раз, каждый раз уменьшая диапазон просмотра
на один элемент.Количество сравнений n-1+n-2+n-3+…+1 = n(n-1)/2
Количество присваиваний 3(n-1+n-2+n-3+…+1) = 3n(n-1)/2
T(n) = n(n-1)/2 + 3n(n-1)/2
Слайд 34
Сортировка выбором
1. Найти максимальный элемент (max) в массиве
(arr).
2. Поместить его на последнее место (j).
3. Элемент, находившийся
в конце массива переместить на место, где прежде находился max.4. Уменьшить просматриваемую область массива на единицу (j – 1).
5. Снова найти максимальный элемент в оставшейся области.
6. Поместить его в конец просматриваемой области массива.
и т.д.
Слайд 36 Максимальное количество перестановок на некотором массиве длины n
будет равно n-1, при этом число сравнений будет одним
и тем же.В общем случае
Количество сравнений n-1+n-2+n-3+…+1 = n(n-1)/2
Количество присваиваний 3(n-1)
T(n) = n(n-1)/2 + 3(n-1)
Слайд 37
Класс сложности: О(n3)
Название: Алгоритмы кубический сложности
Характеристика:
В алгоритмах класса O(n3) каждый элемент обрабатывается С*n3 раз
(цикл-в-цикле-в-цикле)Пример:
умножение матриц размера n*n
Слайд 38
Класс сложности: О(nх)
Название: Полиномиальные алгоритмы
Характеристика:
Все вышеперечисленные классы являются подклассами общего класса: O(nx), где
х - любое (целое) число.Это класс алгоритмов, работающих с полиномиальной скоростью (временная сложность которого выражается некоторой полиномиальной функцией от размера задачи n).
Также этот класс алгоритмов называют Р-класс.
Слайд 39
В рамках теории сложности любые алгоритмы,
работающие с полиномиальной скоростью, считаются быстрыми.
Поэтому
очень много исследований посвящено вопросам типа "возможен ли для данной задачи полиномиальный алгоритм"?
Слайд 40
Класс сложности: О(хn) Класс - EXPTIME
Название: Экспоненциальные алгоритмы
Характеристика:
У экспоненциальных алгоритмов сложность увеличивается быстрее
любого полинома.Большинство экспоненциальных алгоритмов – это варианты полного перебора.
Слайд 41
Класс сложности: О(n!)
Название: Факториальные алгоритмы
Примеры:
Такие
алгоритмы в основном, используются в комбинаторике для определения числа
сочетаний, перестановок
Слайд 42
Наряду с алгоритмически неразрешимыми задачами, существуют объективно сложные
задачи - трудоемкость которых сохраняется при любом прогрессе вычислительной
техники
Слайд 44
Вопросы к лекции
1. Какой алгоритм называют эффективным?
2. Почему
для определения сложности алгоритма оценивают не пространственную, а временную
сложность алгоритма?3. Что характеризует асимптотическая оценка сложности алгоритма?
4. В каких случаях алгоритм, имеющий асимптотическую сложность O(n2), может работать быстрее, чем алгоритм с асимптотической сложностью O(n)?
5. Какие классы алгоритмов считаются „медленными“?





























