- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Сложные структуры данных. Связные списки
Содержание
- 2. Структуры, ссылающиеся на себяstruct node { int x; struct node *next;};
- 3. Связный списокСтруктура данных, представляющая собой конечное множество
- 4. Недостатки связного спискаНедостатком связного списка, как и
- 5. Односвязный списокКаждый узел односвязного (однонаправленного связного) списка
- 6. Односвязный списокКаждый из блоков представляет элемент (узел)
- 7. Односвязные и двусвязные спискиОдносвязный список не самый
- 8. Двусвязный списокОсобенность двусвязного списка, что каждый элемент
- 9. Двусвязный списокВозможность двигаться как вперед, так и
- 10. Кольцевой списокЕще один вид связного списка –
- 11. Управление памятьюДля создания и использования динамических структур
- 12. Управление памятьюФункции для управления динамической памятью объявлены
- 13. mallocvoid* malloc (size_t size);Резервирует блоки памяти размером
- 14. freevoid free (void* ptr);Освобождает память, т.е. память
- 15. #include struct node { int x; struct
- 16. int main(){ /* Это менять нельзя,
- 17. /* Создаёт новый узел в конце
- 18. conductor = root;if ( conductor != NULL
- 19. conductor = root;while ( conductor != NULL
- 20. Очистка памяти struct node *temp; temp =
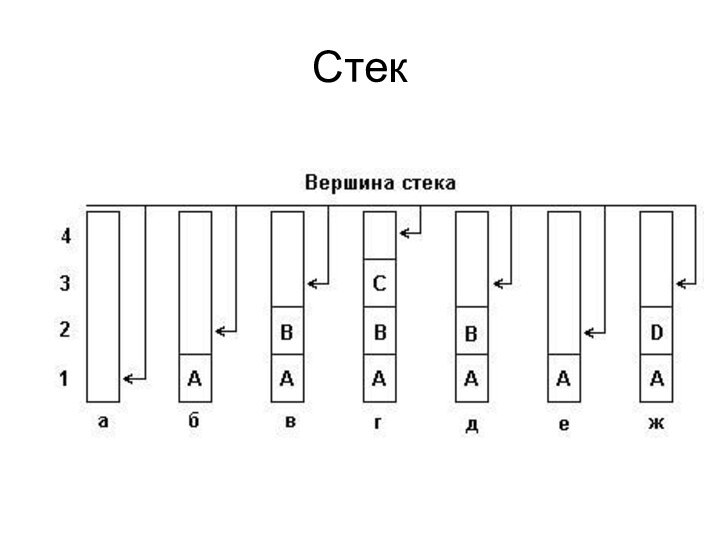
- 21. Стек Стеком называется структура данных, организованная по принципу LIFO – last-in, first-out , т.е.
- 22. Стек
- 23. Стек Реализация 1на основе массиваДля реализации стека,
- 24. Стек Реализация 2на основе массива с использованием общей структурыstruct Stack{int stack[100];int n;};
- 25. Стек Реализация 3на основе указателейЕсли максимальный размер
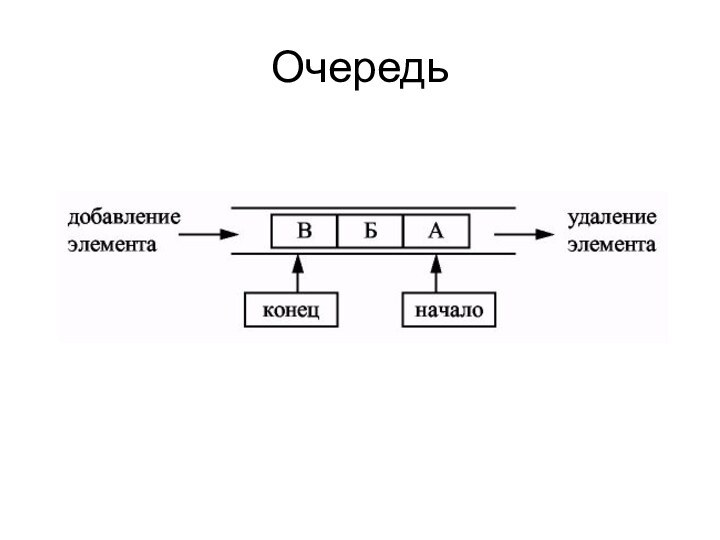
- 26. ОчередьОчередью называется структура данных, организованная по принципу FIFO – first-in, first-out , т.е.
- 27. Очередь
- 28. Очередь реализацияДля реализации очереди необходимо знать первый
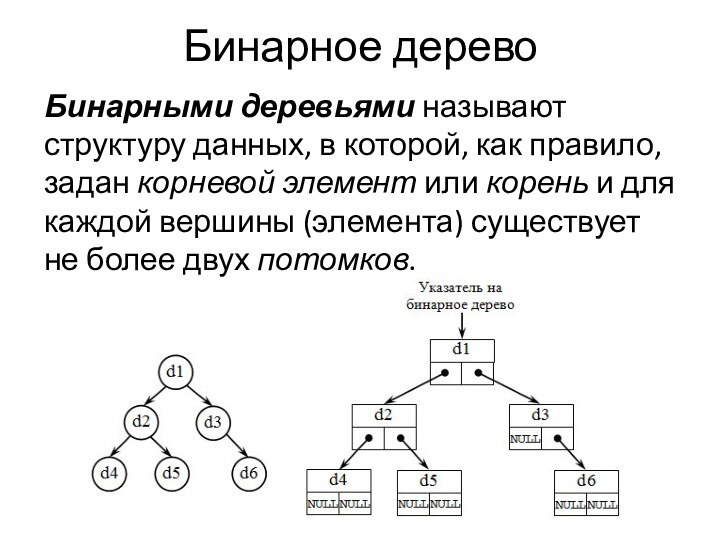
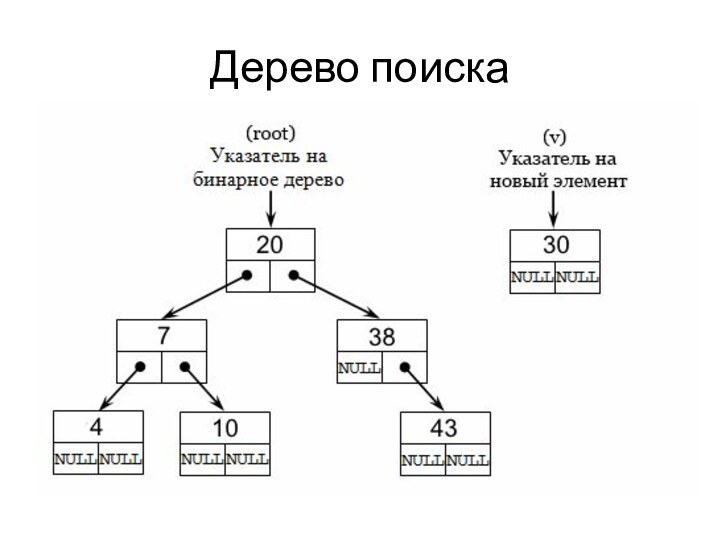
- 29. Бинарное деревоБинарными деревьями называют структуру данных, в которой,
- 30. Бинарное дерево реализацияstruct STree{ int value; struct STree *prev; struct
- 31. Бинарное деревоБинарное дерево называется деревом поиска, если для
- 32. Дерево поискаПоиск элементаstruct STree *Find(struct STree *root, int v){if(root==NULL)return NULL;if(root->value==v)return root;if(root->value>=v)return Find(root->right,v);else return Find(root->left, v);};
- 33. Дерево поиска Добавление элемента struct STree *Insert(struct
- 34. Дерево поиска
- 35. Дерево поискаif(v->value>=root->value)
- 36. Дерево поискаreturn root->right==NULL ?
- 37. Дерево поискаroot->right==NULL ?(v->back=root,v->right=v->left=NULL,root->right=v) : Insert(root->right, v);
- 38. Дерево поискаif(v->value>=root->value)
- 39. Дерево поиска return root->left==NULL ?
- 40. Дерево поискаroot->left==NULL ? (v->prev=root,v->right=v->left=NULL,root->left=v) : Insert(root->left, v);
- 41. Функция Insert добавляет элемент в бинарное дерево
- 42. Аргументы командной строки При запуске программы через консоль
- 43. Аргументы командной строки Обратиться к аргументам командной строки
- 44. Аргументы командной строки#include int main(int argc, char
- 45. Скачать презентацию
- 46. Похожие презентации
Структуры, ссылающиеся на себяstruct node { int x; struct node *next;};






















![Сложные структуры данных. Связные списки Стек Реализация 2на основе массива с использованием общей структурыstruct Stack{int stack[100];int n;};](/img/tmb/15/1411868/67451ea49d996a7f849f00455c1e4926-720x.jpg)














![Сложные структуры данных. Связные списки Аргументы командной строки#include int main(int argc, char *argv[]){ if(argc > 1) { printf(](/img/tmb/15/1411868/f4a58626a6acaef52b3206263a38de22-720x.jpg)
Слайд 3
Связный список
Структура данных, представляющая собой конечное множество упорядоченных
элементов (узлов), связанных друг с другом посредством указателей, называется
связным списком.Каждый элемент связного списка содержит поле с данными, а также указатель на следующий и/или предыдущий элемент. Эта структура позволяет эффективно выполнять операции добавления и удаления элементов для любой позиции в последовательности.
Слайд 4
Недостатки связного списка
Недостатком связного списка, как и других
структур типа «список», в сравнении его с массивом, является
отсутствие возможности работать с данными в режиме произвольного доступа, т. е. список – структура последовательно доступа, в то время как массив – произвольного.
Слайд 5
Односвязный список
Каждый узел односвязного (однонаправленного связного) списка содержит
указатель на следующий узел. Из одной точки можно попасть
лишь в следующую точку, двигаясь тем самым в конец. Так получается своеобразный поток, текущий в одном направлении.
Слайд 6
Односвязный список
Каждый из блоков представляет элемент (узел) списка.
Здесь и далее Head list – заголовочный элемент списка
(для него предполагается поле next). Он не содержит данные, а только ссылку на следующий элемент. На наличие данных указывает поле info, а ссылки – поле next. Признаком отсутствия указателя является поле null.
Слайд 7
Односвязные и двусвязные списки
Односвязный список не самый удобный
тип связного списка, т. к. из одной точки можно
попасть лишь в следующую точку, двигаясь тем самым в конец. Когда в двусвязном списке, кроме указателя на следующий элемент есть указатель на предыдущий.
Слайд 8
Двусвязный список
Особенность двусвязного списка, что каждый элемент имеет
две ссылки: на следующий и на предыдущий элемент, позволяет
двигаться как в его конец, так и в начало.Операции добавления и удаления здесь наиболее эффективны, чем в односвязном списке, поскольку всегда известны адреса тех элементов списка, указатели которых направлены на изменяемый элемент. Но добавление и удаление элемента в двусвязном списке, требует изменения большого количества ссылок, чем этого потребовал бы односвязный список.
Слайд 9
Двусвязный список
Возможность двигаться как вперед, так и назад
полезна для выполнения некоторых операций, но дополнительные указатели требуют
задействования большего количества памяти, чем таковой необходимо в односвязном списке.
Слайд 10
Кольцевой список
Еще один вид связного списка – кольцевой
список. В кольцевом односвязном списке последний элемент ссылается на
первый. В случае двусвязного кольцевого списка – плюс к этому первый ссылается на последний. Таким образом, получается зацикленная структура.
Слайд 11
Управление памятью
Для создания и использования динамических структур требуется
динамическое распределение памяти — возможность получения памяти для хранения
новых узлов и освобождать память для удаления узлов.
Слайд 12
Управление памятью
Функции для управления динамической памятью объявлены в
stdlib.h
функция для выделения памяти:
void* malloc (size_t size);
Функция для освобождения
ранее выделенной памяти:void free (void* ptr);
Слайд 13
malloc
void* malloc (size_t size);
Резервирует блоки памяти размером size
байт памяти и возвращает указатель на начало зарезервированного участка
памяти.Например:
newPtr = malloc (sizeof(struct node));
sizeof(struct node) определяет размер в байтах структуры типа struct node, а malloc выделяет новый блок памяти размером в sizeof(struct node) и возвращает указатель на выделенную память в newPtr. Если памяти для выделения не достаточно, то malloc возвращает указатель на NULL
Слайд 14
free
void free (void* ptr);
Освобождает память, т.е. память возвращается
системе, и в дальнейшем её можно будет выделить снова.
Например:
free
(newPtr);После того как выделенная память больше не нужна необходимо её освободить при помощи free. Так же это не обходимо делать перед завершением программы, если память ещё не была освобождена.
Слайд 15
#include
struct node {
int x;
struct node
*next;
};
int main()
{
/* Обычная структура */
struct
node *root; /* Теперь root указывает на структуру node */
root = (struct node *) malloc( sizeof(struct node) );
/* Узел root указывает на следующий элемент, которого пока нет */
root->next = NULL;
/* Использование оператора -> позволяет изменять узел структуры, на которую он указывает */
root->x = 5;
free ( root );
return 0;
}
Слайд 16
int main()
{
/* Это менять нельзя, т.к.
тогда мы потеряем список в памяти */
struct
node *root; /* Это указывает на каждый элемент списка, пока мы пробегаем по нему */
struct node *conductor;
root = malloc( sizeof(struct node) );
root->next = NULL;
root->x = 12;
conductor = root;
if ( conductor != NULL ) {
while ( conductor->next != NULL)
{
conductor = conductor->next;
}
}
Слайд 17
/* Создаёт новый узел в конце */
conductor->next = malloc( sizeof(struct node) );
conductor = conductor->next; if ( conductor == NULL )
{
printf("Не хватает памяти!\n");
return 0;
}
/* инициализируем память */
conductor->next = NULL;
conductor->x = 42;
return 0;
}
Слайд 18
conductor = root;
if ( conductor != NULL )
{
/*убедимся, что существует место старта*/
while (
conductor->next != NULL ) {printf( "%d\n", conductor->x);
conductor = conductor->next;
}
printf( "%d\n", conductor->x );
}
Слайд 19
conductor = root;
while ( conductor != NULL )
{
printf( "%d\n", conductor->x );
conductor =
conductor->next;}
Слайд 20
Очистка памяти
struct node *temp;
temp = root->ptr;
free(root); /* освобождение памяти текущего корня*/
root =
temp; // новый корень списка
Слайд 21
Стек
Стеком называется структура данных, организованная по принципу LIFO – last-in, first-out , т.е. элемент,
попавшим в множество последним, должен первым его покинуть.
При
практическом использовании часто налагается ограничение на длину стека, т.е. требуется, чтобы количество элементов не превосходило заранее определенное целое число N
Слайд 23
Стек
Реализация 1
на основе массива
Для реализации стека, состоящего не
более чем из 100 чисел, следует определить массив, состоящий из 100 элементов и
целую переменную, указывающую на вершину стека (ее значение будет также равно текущему числу элементов в стеке)int stack[100], n=0;
Слайд 24
Стек
Реализация 2
на основе массива с использованием общей структуры
struct
Stack{
int stack[100];
int n;
};
Слайд 25
Стек
Реализация 3
на основе указателей
Если максимальный размер стека можно
выяснить только после компиляции программы, то память под стек
нужно выделять динамически. При этом, вершину стека можно указывать не индексом в массиве, а указателем на вершину. Для этого следует определить следующие переменныеint *stack, *head;
или
struct SStack{
int *stack;
int *n;
};
Слайд 26
Очередь
Очередью называется структура данных, организованная по принципу FIFO – first-in, first-out , т.е. элемент,
попавшим в множество первым, должен первым его и покинуть.
При практическом использовании часто налагается ограничение на длину очереди, т.е. требуется, чтобы количество элементов не превосходило заранее определенное целое число N
Слайд 28
Очередь
реализация
Для реализации очереди необходимо знать первый и последний
элемент находящийся в ней. Например, для реализации стандартной очереди
из менее чем 100 целых чисел определить следующие данные#define N 100
int array[N], begin=0,end=0;
Соответственно при добавлении элементов в очередь переменная end будет увеличиваться, а при изъятии их из очереди увеличиваться будет begin.
Слайд 29
Бинарное дерево
Бинарными деревьями называют структуру данных, в которой, как
правило, задан корневой элемент или корень и для каждой вершины (элемента) существует не
более двух потомков.
Слайд 30
Бинарное дерево
реализация
struct STree{
int value;
struct STree *prev;
struct STree *left,
*right;
};
здесь указатель prev указывает на родительский элемент данной вершины, а left и right – на
двух потомков, которых традиционно называют левым и правым. Величина value называется ключом вершины.
Слайд 31
Бинарное дерево
Бинарное дерево называется деревом поиска, если для любой
вершины дерева a ключи всех вершин в правом поддереве больше или
равны ключа a, а в левом – меньше. Неравенства можно заменить на строгие, если известно, что в дереве нет равных элементов.
Слайд 32
Дерево поиска
Поиск элемента
struct STree *Find(struct STree *root, int
v){
if(root==NULL)return NULL;
if(root->value==v)return root;
if(root->value>=v)return Find(root->right,v);
else return Find(root->left, v);
};
Слайд 33
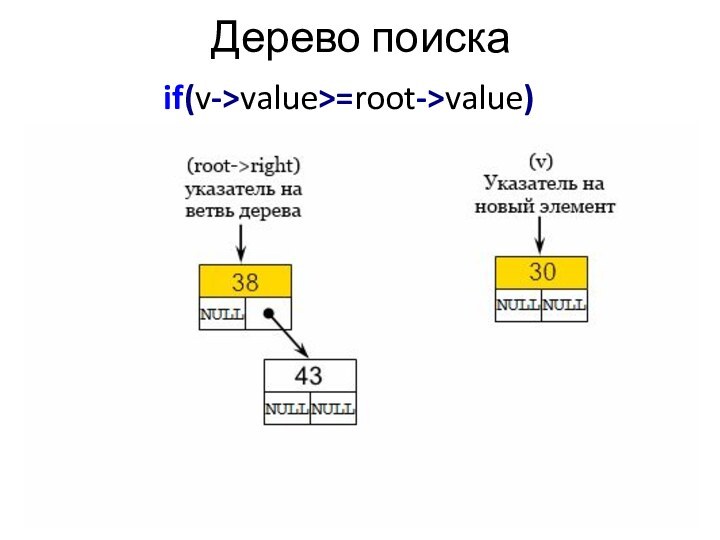
Дерево поиска
Добавление элемента
struct STree *Insert(struct STree *root, struct
STree *v){
if(v->value>=root->value)
return root->right==NULL ?
(v->prev=root,
v->right=v->left=NULL, root->right=v) : Insert(root->right, v);else
return root->left==NULL ?
(v->prev=root,v->right=v->left=NULL,root->left=v) : Insert(root->left, v);
};
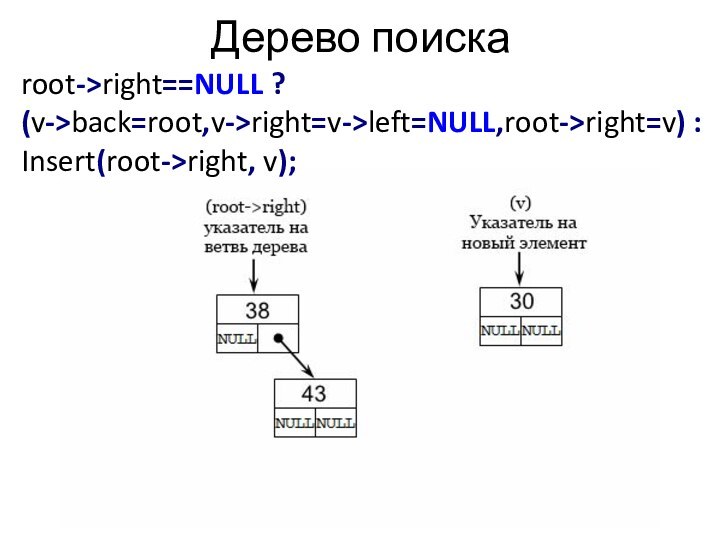
Слайд 37
Дерево поиска
root->right==NULL ?
(v->back=root,v->right=v->left=NULL,root->right=v) : Insert(root->right, v);
Слайд 40
Дерево поиска
root->left==NULL ?
(v->prev=root,v->right=v->left=NULL,root->left=v) : Insert(root->left, v);
Слайд 41 Функция Insert добавляет элемент в бинарное дерево поиска
и возвращает указатель на добавляемый элемент.
Дерево поиска
Добавление элемента
Слайд 42
Аргументы командной строки
При запуске программы через консоль возможно
передать в программу данные, называемые Аргументы командной строки, в
виде строк.Они могут быть использованы во время работы программы
Слайд 43
Аргументы командной строки
Обратиться к аргументам командной строки в
программе возможно через специальные переменные int argc и char
*argv[]argc – число переданных аргументов,
argv – массив строк равный числу аргументов.
При вызове программы всегда есть один аргумент имя запущенной программы.
Слайд 44
Аргументы командной строки
#include
int main(int argc, char *argv[]){
if(argc
> 1) {
printf("Вы ввели много чего");
}
printf("Но это точно имя
этой программы: %s", argv[0]);return 0;
}