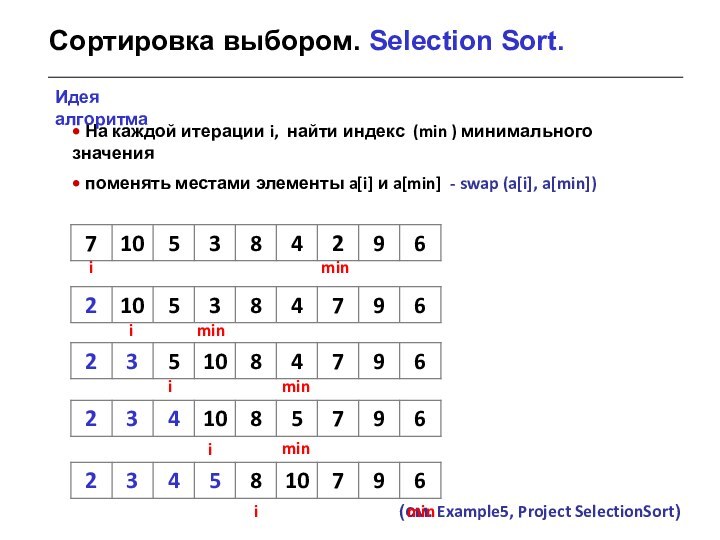
i, найти индекс (min ) минимального значения
поменять местами
элементы a[i] и a[min] - swap (a[i], a[min])Идея алгоритма
(см. Example5, Project SelectionSort)
i
min
i
min
i
min
i
min
i
min
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть











Идея алгоритма
(см. Example5, Project SelectionSort)
i
min
i
min
i
min
i
min
i
min
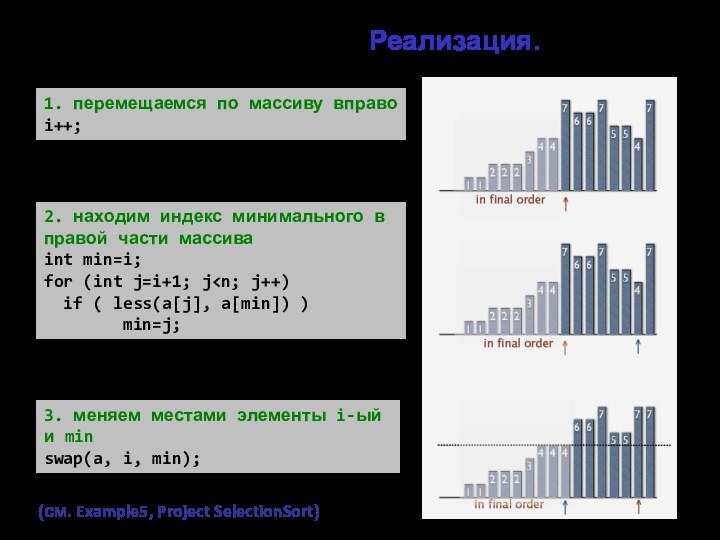
3. меняем местами элементы i-ый и min
swap(a, i, min);
Плюсы: Количество перестановок минимально
Минусы: Очень высокая вычислительная сложность O(N2)
Идея алгоритма
(см. Example5, Project InsertionSort)
Плюсы:
эффективен на небольших наборах данных (до десятков элементов)
эффективен на частично-отсортированных наборах данных
Минусы: Очень высокая вычислительная сложность O(N2)
Идея алгоритма
(см. Example5, Project BubbleSort)
2. Сравниваем все пары соседних элементов a[j], a[j-1]. Если порядок нарушен, выполняем перестановку
for (int j=n-1; j>i; j--)
if ( less(a[j], a[j-1]) )
{
swap(a, j, j-1);
swapped=true;
}
3. Если перестановок не было, то завершаем проходы, иначе следующий проход (i++)
if (!swapped) break;