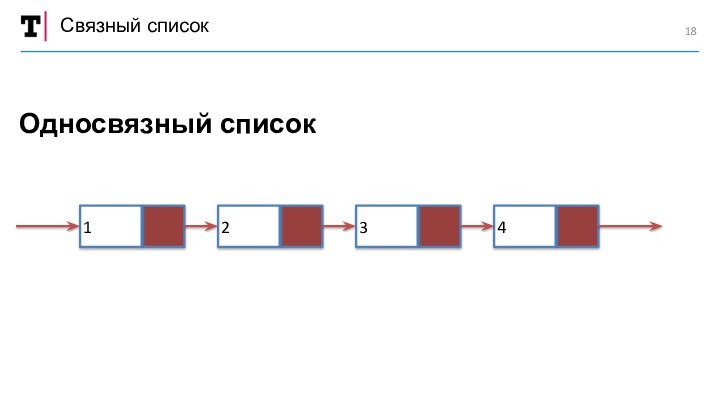
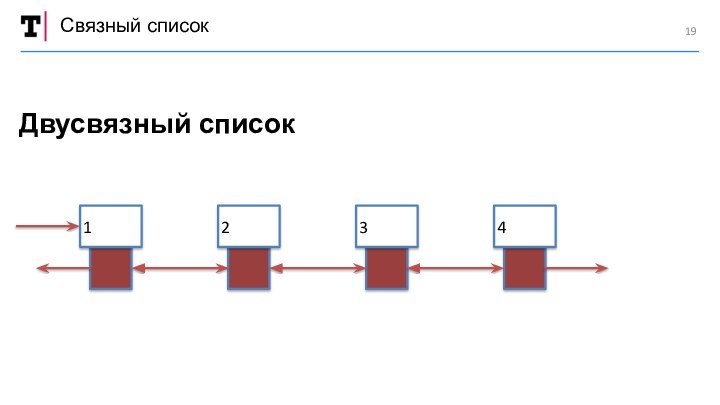
двунаправленные списки
Поиск, добавление элементов, слияние списков
Абстрактные типы данных
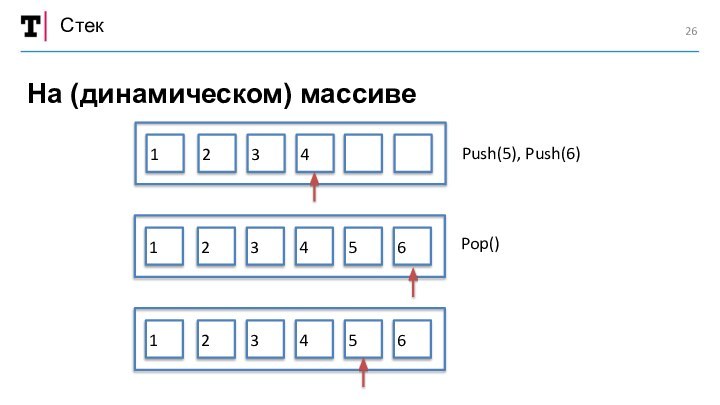
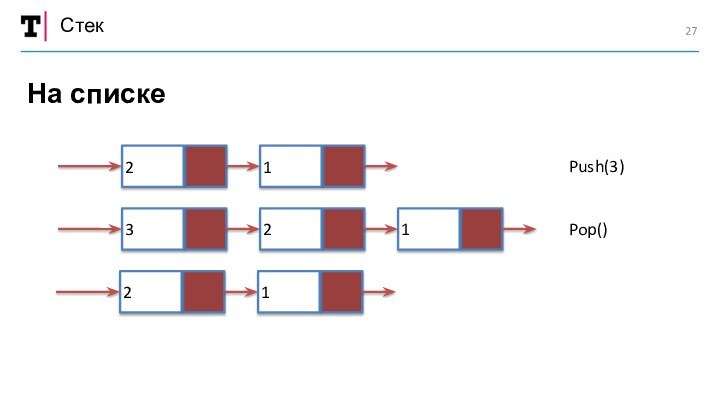
«Стек»
Амортизированное время
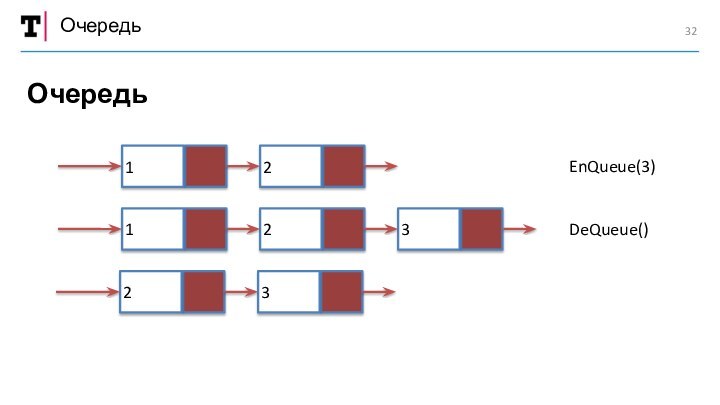
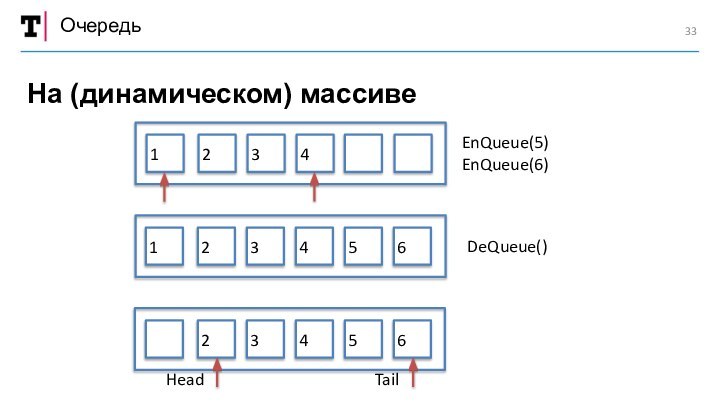
работы«Очередь»
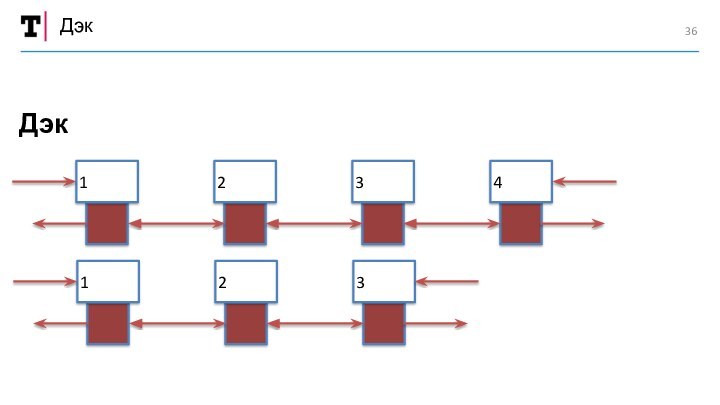
«Дек»
Способы реализации
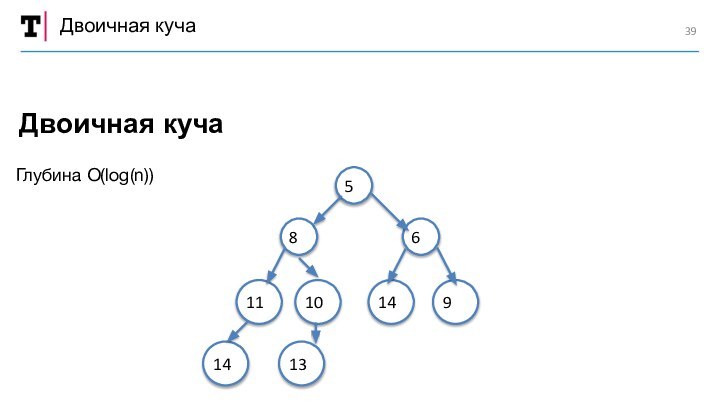
Структура данных «Двоичная куча»
АТД «Очередь с приоритетом»




























![Структуры данных: динамический массив, стек, очередь, дек, бинарная куча Двоичная кучаДвоичный подвешенный [связный ациклический граф — дерево],для которого выполнены условия:1 — Значение](/img/tmb/15/1480766/e1982321109b2fb847b6cf45c312ad4f-720x.jpg)
![Структуры данных: динамический массив, стек, очередь, дек, бинарная куча Двоичная кучаУдобно хранить в массивеa[0] — кореньа дети a[i] - a[2i +](/img/tmb/15/1480766/e7a0caf7157dfc366dcd7e70afeb8cdd-720x.jpg)







![Структуры данных: динамический массив, стек, очередь, дек, бинарная куча Двоичная кучаДоказательство времени работы…Построение кучи [2]](/img/tmb/15/1480766/d7e573417937057c696e9bd37c5e3434-720x.jpg)
































