Слайд 2
- отказ (ренегатство) - пользователь А заявляет, что
он не посылал сообщение пользователю В, хотя на самом
деле посылал;
- модификация (переделка) - пользователь В изменяет сообщение и утверждает, что данные измененного сообщения посылал ему пользователь А;
- подделка (подмена) - пользователь В формирует сообщение и утверждает, что данные сформированного сообщения посылает ему пользователь А;
активный перехват - пользователь С перехватывает сообщение между пользователями
Слайд 3
А и В с целью скрытой модификации;
-
маскировка (имитация, маскарад) - пользователь С посылает сообщение пользователю
В от имени А;
повтор - пользователь С повторяет ранее переданное сообщение, которое пользователь А посылал ранее В.
Функционально цифровая подпись аналогична обычной рукописной подписи и обладает ее основными достоинствами:
- удостоверяет, что подписанный текст исходит от лица, поставившего подпись;
Слайд 4
- не дает самому этому лицу возможности отказаться
от обязательств, связанных с подписанным текстом;
- гарантирует целостность
подписанного текста.
ЭЦП представляет собой относительно небольшое количество дополнительной цифровой информации, передаваемой вместе с подписываемым текстом.
ЭЦП реализуется при помощи асимметричных алгоритмов шифрования и хэш-функций.
Технология применения системы ЭЦП предполагает наличие сети абонентов, посылающих друг другу подписанные электронные документы.
Слайд 5
Для каждого абонента генерируется пара ключей: секретный и
открытый. Секретный ключ хранится абонентом в тайне и используется
им для формирования ЭЦП. Открытый ключ известен всем другим пользователям и предназначен для проверки ЭЦП получателем подписанного электронного документа.
Таким образом, ЭЦП - данные, присоединяемые к передаваемому сообщению и подтверждающие, что владелец подписи заверил данное сообщение.
Слайд 6
При этом получатель сообщения может проверить, что автором
сообщения является именно владелец подписи, и что данные не
были изменены в процессе передачи. В общем случае под ЭЦП понимается числовое значение, вычисляемое по сообщению с использованием секретного ключа подписывающего. Проверка ЭЦП осуществляется общеизвестной процедурой на основании открытого ключа.
Система ЭЦП включает две основные процедуры:
- формирования цифровой подписи;
- проверка цифровой подписи.
Слайд 7
Процедура формирования цифровой подписи.
На подготовительном этапе этой
процедуры абонент А - отправитель сообщения - генерирует пару
ключей: секретный ключ kА и открытый ключ КА. Открытый ключ рассылается остальным абонентам сети для проверки подписи.
Для формирования цифровой подписи отправитель А прежде всего вычисляет значение хэш-функции h(M) подписываемого текста М. Хэш-функция служит для сжатия исходного подписываемого текста М в дайджест т - относительно короткое число, состоящее из фиксированного небольшого числа битов и характеризующее весь текст М в целом.
Слайд 8
Под хэш-функцией понимается математическое или алгоритмическое преобразование заданного
блока данных. Она обладает следующими свойствами: имеет бесконечную область
определения, конечную область значений, необратима, изменение входного потока информации на один бит меняет около половины всех бит выходного потока.
К дайджесту т добавляется информация о том, кто подписывает документ, штамп времени и прочее. Далее абонент А шифрует получившуюся строку своим секретным ключом kА. Получившийся зашифрованный набор бит и представляет собой подпись для данного текста М.
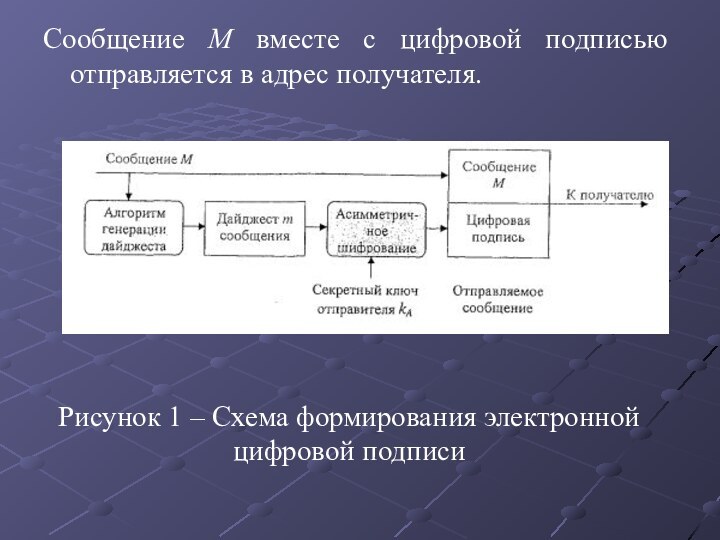
Слайд 9
Сообщение М вместе с цифровой подписью отправляется в
адрес получателя.
Рисунок 1 – Схема формирования электронной цифровой подписи
Слайд 10
Процедура проверки цифровой подписи.
При проверке ЭЦП абонент
В - получатель сообщения М - расшифровывает принятый дайджест
т открытым ключом КА отправителя А. Кроме того, получатель сам вычисляет с помощью хэш-функции h(M) дайджест т' принятого сообщения М и сравнивает его с расшифрованным. Если т и т' совпадают, то цифровая подпись является подлинной. В противном случае либо подпись подделана, либо изменено содержание сообщения.
Слайд 11
Рисунок 2 - Схема проверки электронной цифровой подписи
Слайд 12
Принципиальным моментом в системе ЭЦП является невозможность подделки
ЭЦП пользователя без знания его секретного ключа. Поэтому необходимо
защитить секретный ключ от НСД.
Важно отметить, что с точки зрения конечного пользователя процесс формирования и проверки цифровой подписи отличается от процесса криптографического закрытия передаваемых данных следующими особенностями.
Слайд 13
При формировании цифровой подписи используется закрытый
ключ отправителя, тогда как при
зашифровке используется открытый ключ получателя. При проверке цифровой подписи используется открытый ключ отправителя, а при расшифровке - закрытый ключ получателя.
Проверить сформированную подпись может любое лицо, так как ключ проверки является открытым. При положительном результате проверки подписи делается заключение о подлинности и целостности полученного сообщения, т.е. о том, что это сообщение действительно отправлено тем или иным отправителем, и не было модифицировано при передаче по сети.
Слайд 14
Схема подписи на основе алгоритма RSA.
Для создания подписи
сообщения М отправитель:
1. Вычисляет сжатый образ (дайджест сообщения, хэш-образ)
R = Н(М) с помощью хэш-функции Н.
2. Зашифровывает полученный сжатый образ на своем секретном ключе и получает подпись
S=Rdmodn, где {d,n}-закрытый ключ отправителя.
Для проверки подписи получатель:
1. Расшифровывает подпись S на открытом ключе отправителя, то есть вычисляет R' = Semodn, где {е, п} - открытый ключ отправителя.
Слайд 15
2. Вычисляет сжатый образ R = Н(М) с
полученного сообщения с помощью той же самой хэш-функции Н,
которую использовал отправитель.
3. Сравнивает полученные значения R и R’, если они совпадают, то подпись верна.
Таким образом, ЭЦП - набор электронных цифровых символов, подтверждающий достоверность электронного документа, его принадлежность и неизменность содержания.
Закрытый ключ ЭЦП - последовательность электронных цифровых символов, известная владельцу подписи и предназначенная для создания ЭЦП.
Слайд 16
Открытый ключ ЭЦП - последовательность электронных цифровых символов,
доступная любому лицу и предназначенная для подтверждения подлинности ЭЦП
в электронном документе.
Слайд 17
Цифровая подпись на основе алгоритма Эль-Гамаля
Алгоритм Эль-Гамаля также
можно использовать для формирования цифровой подписи. Группа пользователей выбирает
общие параметры Р и А. Затем каждый абонент группы выбирает свое секретное число Хi, 1<Хi<Р-1, и вычисляет соответствующее ему открытое число
Таким образом, каждый пользователь получает пару (закрытый ключ; открытый ключ) = (Хi,Yi).
Слайд 18
Пусть пользователь 1 хочет подписать свое сообщение цифровой
подписью и передать его пользователю 2. В этом случае
алгоритм действий следующий.
Первый пользователь выбирает случайное секретное число k, взаимно простое с Р-1, и вычисляет число
Затем с помощью расширенного алгоритма Евклида необходимо найти значение b в следующем уравнении:
m = (X1 * a +k * b) mod (P-1)
Пара чисел (a, b) будет цифровой подписью сообщения m.
Слайд 19
Сообщение m вместе с подписью (a, b) отправляется
пользователю 2.
Пользователь 2 получает сообщение m и с
использованием открытого ключа первого абонента Y1 вычисляет два числа по следующим формулам:
Если с1=с2, то цифровая подпись первого пользователя верная. Для подписывания каждого нового сообщения должно каждый раз выбираться новое значение k.
Слайд 20
Подписи, созданные с использованием алгоритма Эль-Гамаля, называются рандомизированными,
так как для одного и того же сообщения с
использованием одного и того же закрытого ключа каждый раз будут создаваться разные подписи (a,b), поскольку каждый раз будет использоваться новое значение k. Подписи, созданные с применением алгоритма RSA, называются детерминированными, так как для одного и того же сообщения с использованием одного и того же закрытого ключа каждый раз будет создаваться одна и та же подпись.
Слайд 21
Пример вычисления и проверки цифровой подписи
Пусть абоненты, обменивающиеся
через Интернет зашифрованными сообщениями, имеют следующие общие параметры: Р
= 11, А = 7.
Один из пользователей этой системы связи хочет подписать свое сообщение m=5 цифровой подписью, сформированной по алгоритму Эль-Гамаля. Вначале он должен выбрать себе закрытый ключ, например, Х1=3 и сформировать открытый ключ Y1 = 73mod11= 2. Открытый ключ может быть передан всем заинтересованным абонентам или помещен в базу данных открытых ключей системы связи.
Слайд 22
Затем пользователь выбирает случайное секретное число k, взаимно
простое с Р-1. Пусть k=9 (9 не имеет общих
делителей с 10). Далее необходимо вычислить число
После этого с помощью расширенного алгоритма Евклида находится значение b в уравнении:
Решением последнего уравнения будет значение b=9.
Таким образом, пара чисел (8, 9) будет цифровой подписью сообщения m=5.
Слайд 23
Так как с1=с2, то цифровая подпись первого пользователя
в сообщении m=5 верная.
Если любой другой пользователь сети желает
проверить цифровую подпись в сообщении, он должен получить из базы данных открытый ключ первого пользователя (он равен 2), вычислить два числа с1 и с2 и сравнить их.
Слайд 24
Стандарты на алгоритмы цифровой подписи
Стандарт цифровой подписи DSS
Во
многих странах сегодня существуют стандарты на электронную (цифровую) подпись.
Стандарт цифровой подписи DSS (Digital Signature Standard – DSS) был принят в США в 1991 году и пересмотрен в 1994 году. В основе стандарта лежит алгоритм, называемый DSA (Digital Signature Algorithm) и являющийся вариацией подписи Эль-Гамаля. В алгоритме используется однонаправленная хэш-функция H(m). В качестве хэш-алгоритма стандарт DSS предусматривает использование алгоритма SHA-1.
Слайд 25
Рассмотрим сам алгоритм генерации ЭЦП. Вначале для группы
абонентов выбираются три общих (несекретных) параметра р, q и
a:
параметр р должен быть простым числом длиной от 512 до 1024 бит.
q – простое число длиной 160 бит; между p и q должно выполняться соотношение p = bq + l для некоторого целого b.
число а, удовлетворяющее неравенству 1 < a < p-1 и являющееся корнем уравнения aqmod p = l.
Зная эти числа, каждый абонент системы случайно выбирает число х, удовлетворяющее неравенству 0<х
Слайд 26
Число х будет секретным ключом пользователя, а число
у — открытым ключом. Вычислить у по известному х
довольно просто. Однако, имея открытый ключ у, вычислительно невозможно определить х, который является дискретным логарифмом у по основанию q .
Пусть имеется сообщение m, которое один из пользователей желает подписать. Для генерации подписи пользователь должен выполнить следующие действия:
1. Вычислить значение хэш-функции h = H(m) для сообщения m. Значение хэш-функции должно лежать в пределах 0 < h < q.
Слайд 27
2. Затем сгенерировать случайное число k, 0
k < q.
3. Вычислить r = (akmod p)
mod q.
4. Определить s = [k-1(H(m) + x*r)] mod q
В результате пользователь получит для сообщения m подпись, состоящую из пары чисел (r,s). Сообщение вместе с подписью может быть послано любому другому абоненту системы. Проверить подпись можно следующим образом:
1. Вычислить значение хэш-функции h = H(m) для сообщения m.
2. Проверить выполнение неравенств 0 < r < q,
0 < s < q.
Слайд 28
3. Вычислить w = s-1 mod q ;
4. u1 = [H(m) * w] mod q
5. u2
= r * w mod q
6. v = [(аu1 * yu2) mod p] mod q
Проверить выполнение равенства v = r. Если v = r, то подпись считается подлинной, иначе подпись считается недействительной.
В силу сложности вычисления дискретных логарифмов злоумышленник не может восстановить k из r или х из s, а следовательно, не может подделать подпись. По той же самой причине автор сообщения не сможет отказаться от своей подписи, так как никто кроме него не знает закрытого ключа х.
Слайд 29
Стандарт цифровой подписи ГОСТ Р34.10-94
В России принят стандарт
ГОСТ Р34.10-94 "Информационная технология. Криптографическая защита информации. Процедуры выработки
и проверки электронной цифровой подписи на базе асимметричного криптографического алгоритма". В этом стандарте используется алгоритм, аналогичный алгоритму, реализованному в стандарте DSS.
Вначале, так же как и по стандарту DSS, для группы абонентов выбираются три общих (несекретных) параметра р, q и a.
Слайд 30
По-разному вычисляется компонента s подписи. В ГОСТ Р34.10-94
компонента s вычисляется по формуле
s = (k( H(m) +
x( r) mod q,
а в DSS компонента s вычисляется по формуле
s = [k -1 ( (H(m) + x(r))] mod q.
Последнее отличие приводит к соответствующим отличиям в формулах для проверки подписи.
В результате процедура проверки подписи по ГОСТ Р34.10-94 заключается в следующем. Получив [m, (r, s)], получатель вычисляет
w = H(m)-1mod q,
Слайд 31
u1 = w * s mod q,
u2 =
(q-r) * w mod q,
v = [(аu1 * yu2)
mod p] mod q.
Затем проверяется равенство вычисленного значения v и полученного в составе ЭЦП параметра r. Подпись считается корректной, если v = r.
Слайд 32
Пример создания и проверки подписи по стандарту ГОСТ
Р34.10-94
Пусть p = 23, q = 11, a =6
(проверяем: 611mod 23 = l )
Создание подписи.
Предположим, пользователь А выбрал в качестве закрытого ключа число х=8. После этого он вычисляет открытый ключ по формуле y=аxmod p. То есть y = 68 mod 23 = 18.
Для создания подписи пользователь А выбирает случайное число k = 5.
Пусть результат вычисления хэш-функции для сообщения H(m) = 9.
Подпись сообщения состоит из двух чисел (r, s):
r = (аkmod p) mod q = (65 mod 23) mod 11 = 2,
Слайд 33
s = (k* H(m) + x * r)
mod q = (5*9 + 8*2)mod 11 = 6,
Таким
образом, подпись сообщения состоит из пары чисел (2, 6).
Проверка подписи.
Получив сообщение вместе с подписью (2,6), получатель вычисляет
w = H(m)-1mod q = 9-1mod 11 = 5,
u1 = w * s mod q = 5 * 6 mod 11 = 8,
u2 = (q-r)*w mod q = (11-2)*5 mod 11 = 1,
v = [(аu1*yu2) mod p] mod q =[(68*181)mod 23]mod 11= 2
Так как v = r, то подпись считается верной.
Слайд 34
Функция хэширования
В качестве исходного значения для вычисления ЭЦП
берется не сам электронный документ, а его хэш-значение или
дайджест.
Хэш-значение h(M) - это дайджест сообщения М, т.е. сжатое двоичное представление основного сообщения М произвольной длины.
Функция хэширования (хэш-функция) представляет собой преобразование, на вход которого подается сообщение переменной длины М, а выходом является строка фиксированной длины H= h(M).
Слайд 35
Функция хэширования позволяет сжать подписываемый документ М до
128 и более бит (в частности до 128 или
256 бит), тогда как М может быть размером в мегабайт или более.
Следует отметить, что значение хэш-функции h(M) зависит сложным образом от документа М и не позволяет восстановить сам документ М.
Слайд 36
Функция хэширования обладает следующими свойствами:
- хэш-функция может
быть применена к аргументу любого размера;
выходное значение хэш-функции имеет
фиксированный размер;
хэш-функцию достаточно просто вычислить для любого аргумента; скорость вычисления хэш-функции должна быть такой, чтобы скорость выработки и проверки ЭЦП при использовании хэш-функции была значительно больше, чем при использовании самого сообщения;
Слайд 37
- хэш-функция чувствительна к всевозможным изменения в тексте
М, таким как вставки, выбросы, перестановки и т.п.;
-
хэш-функция однонаправлена, т.е. обладает свойством необратимости, иными словами, задача подбора документа М’ который обладал бы требуемым значением хэш-функции, должна быть вычислительно неразрешима;
вероятность того, что значения хэш-функций двух различных документов (вне зависимости от их длин) совпадут, ничтожно мала, т.е. для любого фиксированного х с вычислительной точки зрения невозможно найти х' для х, такое, что h(x') = h(x).