- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задание бинарных деревьев с помощью массивов
Содержание
- 2. СодержаниеЗадание полного бинарного дереваЗадание произвольного бинарного дереваЗадание двоичного дерева поискаОбходы дерева
- 3. Задание полного бинарного дереваНазадМеню В виде массива проще
- 4. НазадМеню Для каждой i – ой вершины, начиная
- 5. Задание произвольного бинарного деревоНазадМеню Часто для решения той
- 6. НазадМеню В отличие от полного дерева в произвольном
- 7. НазадМеню После этого остаётся только задать отношения «отец
- 8. остаемся на четвертой вершине и считываем
- 9. Задание двоичного дерева поиска Рассмотрим задание двоичного дерева
- 10. Берем первый элемент, он будет корнем
- 11. НазадМеню В результате получится следующее двоичное дерево поиска
- 12. Обходы дерева Для того чтобы просмотреть информационные поля
- 13. Алгоритмы обхода дерева: НазадМенюПрямой левый обходПрямой правый
- 14. Прямой левый обход дерева Алгоритм прямого левого обхода
- 15. Прямой правый обход дерева Алгоритм прямого правого обхода
- 16. ПримерВыводя на экран значения вершин бинарного дерева
- 17. Примеры использования прямых обходов: решение задачи методом
- 18. Обратный левый обход Алгоритм обратного левого обхода:Обойти левое
- 19. Пример Выводя на экран значения вершин бинарного дерева
- 20. Обратный правый обход Алгоритм обратного правого обхода:Обойти правое
- 21. Пример Выводя на экран значения вершин бинарного дерева
- 22. Внутренний левый обход Алгоритм внутреннего левого обхода:Обойти левое
- 23. Пример Выводя на экран значения вершин бинарного дерева
- 24. Внутренний правый обход Алгоритм внутреннего правого обхода:Обойти правое
- 25. ПримерВыводя на экран значения вершин бинарного дерева
- 26. Обходы дерева по уровням Для того чтобы осуществить
- 27. Обход по уровням, слева на право сверху
- 28. Процедура обхода бинарного дерева по уровням, слева
- 29. Обход по уровням, справа налево сверху внизAEBCDFGIH Выводя
- 30. Процедура обхода бинарного дерева по уровням, справа
- 31. Обход по уровням, слева на право снизу
- 32. Процедура обхода бинарного дерева по уровням, слева
- 33. Обход по уровням, справа налево снизу вверхAEBCDFGIH Выводя
- 34. Скачать презентацию
- 35. Похожие презентации
































Слайд 2
Содержание
Задание полного бинарного дерева
Задание произвольного бинарного дерева
Задание двоичного
дерева поиска
Слайд 3
Задание полного бинарного дерева
Назад
Меню
В виде массива проще всего
представить полное бинарное дерево, так как оно всегда имеет
строго определенное количество вершин на каждом уровне, кроме последнего уровня (например, число узлов в дереве, имеющем три уровня, может быть от 4 до 7).Для задания полного дерева используем три массива: key (для хранения ключей), left (для хранения ссылок на левых потомков вершин), и right (для хранения ссылок на правых потоков вершин).
Пронумеруем вершины полного дерева так, чтобы левый помок любой i – ой вершины имел адрес 2i, а правый потомок любой i – ой вершины имел адрес 2i + 1.
При задании дерева воспользуемся прямым левым обходом. Сначала задаем количество вершин в нашем дереве (n), формируем корень дерева.
Слайд 4
Назад
Меню
Для каждой i – ой вершины, начиная с
корня, проверяем:
1) если 2i
вершины есть левый потомок, т.е. в массив left на i – ое место записываем адрес 2i. Переходим на вершину с адресом 2i. Задаем число, хранящееся в данной вершине и пункт 1) иначе, если 2i > n, значит, у данной вершины нет левого потомка, т.е. в массив left на i – ое место запишем 0 и пункт 2);2) если 2i+1 < n, значит, у данной вершин есть правый потомок, т.е. в массив right на i – ое место записываем адрес 2i+1. Переходим на вершину с адресом 2i+1. Задаем число, хранящееся в данной вершине и пункт 1) иначе, если 2i+1 > n , значит, у данной вершины нет правого потомка, т.е. в массив right на i – ое место запишем 0. Переходим на предыдущую вершину, для которой условия пункта 1) уже проверены, а условия пункта 2) еще нет.
Программа задания полного дерева на языке Паскаль
Слайд 5
Задание произвольного бинарного дерево
Назад
Меню
Часто для решения той или
иной задачи требуется задать не полное, а произвольное (неполное)
дерево.Пусть нужно задать произвольное дерево
(см. рис.):
Значения, хранящиеся в узлах дерева, не имеют принципиального значения, т.е. их можно сгенерировать случайным образом. Для нумерации вершин используем прямой левый обход, поэтому вершины пронумеруем соответственно ( см. рис.).
Слайд 6
Назад
Меню
В отличие от полного дерева в произвольном дереве
на каждом уровне (кроме нулевого уровня) может быть различное
количество вершин, поэтому вид дерева нужно задавать вручную. Сделать это можно с помощью последовательности, например, 0 и 1 (можно использовать любые символы), хранящейся в текстовом файле.Составляется данная последовательность следующим образом: идем по дереву прямым левым обходом:
встаем на первую вершину и смотрим, слева есть вершина, значит, ставим 1 и переходим на вторую вершину;
у второй вершины слева есть вершина, ставим 1 и переходим на третью вершину;
у третьей вершины слева нет вершины, значит, ставим 0, справа у данной вершины тоже нет другой вершины, ставим 0 и возвращаемся на вторую вершину;
у второй вершины справа есть вершина, ставим 1 и переходим на четвертую вершину и т.д.
Процесс закончится когда мы обойдем все вершины.
В результате в нашем файле должна быть записана следующая последовательность: 1 1 1 0 0 0 1 0 1 1 0 0 1 0 0 1 0 1 0 0.
Слайд 7
Назад
Меню
После этого остаётся только задать отношения «отец –
сын». Для хранения левых и правых ссылок используем массивы
left и right соответственно. Заполнение данных массивов происходит следующим образом:стоим на первой вершине и считываем из ранее заготовленного файла первый элемент, т.е. 1, а это значит, что у первой вершины есть левый потомок – вершина №2, следовательно, в массив left на первое место запишется 2;
переходим на вторую вершину и считываем из файла второй элемент, т.е. 1, значит, что у второй вершины есть левый потомок – вершина №3, следовательно, в массив left на второе место запишется 3;
переходим на третью вершину и считываем из файла третий элемент, т.е. 1, значит, что у третьей вершины есть левый потомок – вершина №4, следовательно, в массив left на третье место запишется 1;
переходим на четвертую вершину и считываем из файла четвертый элемент, т.е. 0, значит, что у четвертой вершины нет левого потомка, следовательно, в массив left на четвертое место запишется 0;
Слайд 8 остаемся на четвертой вершине и считываем следующий
элемент из файла, т.е. 0, значит, что у четвертой
вершины нет правого потомка, следовательно, в массив right на четвертое место запишется 0;возвращаемся на третью вершину и считываем следующий элемент из файла, т.е. 0, значит, что у третьей вершины нет правого потомка, следовательно, в массив right на третье место запишется 0;и т.д.
Процесс закончится, когда мы прямым левым обходом обойдем все вершины дерева.
В результате наше дерево будет задано с помощью трех массивов:
Key – в данном массиве будут храниться значения узлов дерева;
Left = [2 3 4 0 0 7 0 0 0 0] – массив правых ссылок;
Right = [9 5 0 0 6 8 0 0 10 0] – массив правых ссылок.
Назад
Меню
Программа задания произвольного дерева на языке Паскаль
Слайд 9
Задание двоичного дерева поиска
Рассмотрим задание двоичного дерева поиска
с помощью массивов.
Как и в предыдущих случаях для хранения
значений узлов, левых и правых ссылок выделяем массивы key, left и right соответственно. Значения элементов, из которых нужно построить дерево поиска удобно хранить в текстовом файле.Пусть нужно построить дерево поиска для следующего набора элементов: 20 15 32 17 13 23 28 16.
Назад
Меню
Слайд 10 Берем первый элемент, он будет корнем нашего
дерева. Для корня левую и правую ссылки объявляем равными
нулю, т.е. пока кроме корня других вершин нет.Берем второй элемент и сравниваем его с корнем: 15<20 и левая ссылка у корня = 0 т.е. слева у 20 нет вершины, поэтому нужно эту вершину создать, записать в неё 15, обнулить левую и правую ссылки второй вершины и создать связь между этими вершинами т.е. в массив left на первое место записать 2.
Берем третий элемент и сравниваем его с элементами нашего дерева, начиная с корня: 32>20, правая ссылка у корня = 0. Следовательно, справа от корня создаем вершину, записываем в неё 32, обнуляем левую и правую ссылки третьей вершины и создаем связь между этими вершинами, т.е. в массив right на первое место записать 3.
Берем четвертый элемент и сравниваем его с элементами нашего дерева, начиная с корня: 17<20, но слева у 20 уже есть вершина №2 (в ней записано 15), поэтому нужно перейти на эту вершину и сравнить ее значение с взятым элементом. 17>15, правая ссылка у второй вершины = 0. Следовательно, справа от неё создаем вершину, записываем в неё 17, обнуляем левую и правую ссылки четвертой вершины и создаем связь между этими вершинами, т.е. в массив right на второе место записываем 4 и т.д. Процесс закончится, когда мы переберем все элементы файла.
Назад
Меню
Слайд 11
Назад
Меню
В результате получится следующее двоичное дерево поиска (см.
рис.), заданное с помощью массивов:
Key = [20 15 32
17 13 23 28 16];Left = [2 5 6 8 0 0 0 0];
Right = [3 4 0 0 0 7 0 0].
20
15
13
17
32
16
23
1
2
5
4
8
3
6
28
7
Программа задания двоичного дерева поиска на языке Паскаль
Слайд 12
Обходы дерева
Для того чтобы просмотреть информационные поля всех
вершин построенного дерева, найти нужный элемент в дереве, отсортировать
элементы дерева и во многих других задачах необходимо совершить так называемый обход дерева (посетить каждую его вершину, причем производить какие-то действия с каждой вершиной можно только 1 раз).В случае, когда бинарное дерево пусто, оно обходится без выполнения каких- либо действий. Чтобы обойти непустое дерево существует несколько алгоритмов.
Рекурсивные алгоритмы прохождения каждого дерева по каждому из способов включают 3 одинаковых процедуры, где нужно найти корень поддерева, левое поддерево текущего корня и правое поддерево текущего корня. Направление обхода однозначно определяет последовательность выполнения указанных процедур.
Назад
Меню
Слайд 13
Алгоритмы обхода дерева:
Назад
Меню
Прямой левый обход
Прямой правый обход
Обратный
левый обход
Обратный правый обход
Внутренний левый обход
Внутренний правый обход
По уровням
слева на право сверху внизПо уровням справа налево сверху вниз
По уровням слева на право снизу вверх
По уровням справа налево снизу вверх
Слайд 14
Прямой левый обход дерева
Алгоритм прямого левого обхода дерева:
Посетить
корень;
Обойти левое поддерево;
Обойти правое поддерево.
Процедура прохождения дерева прямым левым
обходом на языке Паскаль:procedure obxod_1(i:integer);
begin
if i<>0 then begin write(key[i]:4); obxod_1(left[i]); obxod_1(right[i]); end;
end;
Назад
Меню
Список обходов
Слайд 15
Прямой правый обход дерева
Алгоритм прямого правого обхода дерева:
Посетить
корень;
Обойти правое поддерево;
Обойти левое поддерево.
Процедура прохождения дерева прямым правым
обходом на языке Паскаль:procedure obxod_2(i:integer);
begin
if i<>0 then
begin
write(key[i]:4);
obxod_2(right[i]);
obxod_2(left[i]);
end;
end;
Назад
Меню
Слайд 16
Пример
Выводя на экран значения вершин бинарного дерева (см.рис.),
используя прямой правый обход, получим последовательность:
A E G
I H F B D CНазад
Меню
A
E
B
C
D
F
G
I
H
Список обходов
Слайд 17
Примеры использования прямых обходов:
решение задачи методом деления
на части
стратегия "разделяй и властвуй" (Сортировка Фон Hеймана,
быстрая сортировка, одновременное нахождение максимума и минимума последовательности чисел, умножение длинных чисел). Назад
Меню
Список обходов
Слайд 18
Обратный левый обход
Алгоритм обратного левого обхода:
Обойти левое поддерево;
Обойти
правое поддерево;
Посетить корень.
Процедура прохождения дерева обратным левым обходом на
языке Паскаль:procedure obxod_3(i:integer);
begin
if i<>0 then
begin
obxod_3(left[i]);
obxod_3(right[i]);
write(key[i]:4);
end;
end;
Назад
Меню
Слайд 19
Пример
Выводя на экран значения вершин бинарного дерева (см.рис.),
используя обратный левый обход, получим последовательность:
C D B F
H I G E AНазад
Меню
A
E
B
C
D
F
G
I
H
Список обходов
Слайд 20
Обратный правый обход
Алгоритм обратного правого обхода:
Обойти правое поддерево;
Обойти
левое поддерево;
Посетить корень.
Процедура прохождения дерева обратным правым обходом на
языке Паскаль:procedure obxod_4(i:integer);
begin
if i<>0 then
begin
obxod_4(right[i]);
obxod_4(left[i]);
write(key[i]:4);
end;
end;
Назад
Меню
Слайд 21
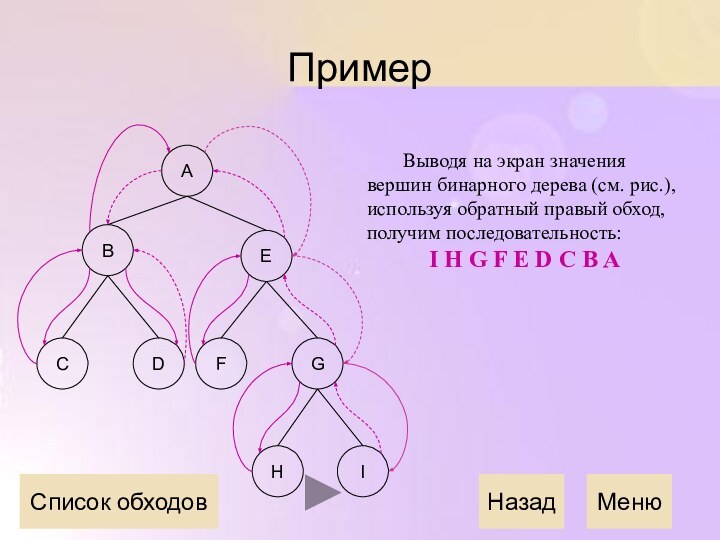
Пример
Выводя на экран значения вершин бинарного дерева (см.
рис.), используя обратный правый обход, получим последовательность:
I H
G F E D C B AНазад
Меню
A
E
B
C
D
F
G
I
H
Список обходов
Слайд 22
Внутренний левый обход
Алгоритм внутреннего левого обхода:
Обойти левое поддерево;
Посетить
корень;
Обойти правое поддерево.
Процедура прохождения дерева внутренним левым обходом на
языке Паскаль:procedure obxod_5(i:integer);
begin
if i<>0 then
begin
obxod_5(left[i]);
write(key[i]:4);
obxod_5(right[i]);
end;
end;
Назад
Меню
Слайд 23
Пример
Выводя на экран значения вершин бинарного дерева (см.рис.),
используя внутренний левый обход, получим последовательность:
C B D
A F E H G IНазад
Меню
Список обходов
Слайд 24
Внутренний правый обход
Алгоритм внутреннего правого обхода:
Обойти правое поддерево;
Посетить
корень;
Обойти левое поддерево.
Процедура прохождения дерева внутренним правым обходом на
языке Паскаль:procedure obxod_6(i:integer);
begin
if i<>0 then
begin
obxod_6(right[i]);
write(key[i]:4);
obxod_6(left[i]);
end;
end;
Назад
Меню
Слайд 25
Пример
Выводя на экран значения вершин бинарного дерева (см.
рис.), используя внутренний правый обход, получим последовательность:
I G
H E F A D B CНазад
Меню
Список обходов
Слайд 26
Обходы дерева по уровням
Для того чтобы осуществить любой
из четырех обходов дерева по уровням необходимо знать, сколько
уровней в дереве (высоту дерева), которое нужно обойти. Если дерево неполное и содержит большое количество вершин, то считать количество уровней вручную очень сложно. Рационально будет использовать специальную процедуру, которая определяет высоту любого бинарного дерева.Процедура вычисления высоты бинарного дерева на языке Паскаль:
procedure H_tree(i,u:integer);
begin
if i<>0 then begin if hend;
По окончанию работы данной процедуры в переменной h будет храниться высота дерева, которое нужно обойти.
Назад
Меню
Слайд 27
Обход по уровням, слева на право сверху вниз
A
E
B
C
D
F
G
I
H
Выводя
на экран значения вершин бинарного дерева (см. рис.), используя
обход по уровням, слева на право сверху вниз, получим последовательность:A B E C D F G H I
Назад
Меню
Слайд 28 Процедура обхода бинарного дерева по уровням, слева на
право сверху вниз на языке Паскаль:
procedure obxod_7(i,u:integer);
begin
if i0 then
begin
if
j = u then write(key[i]:4)Else begin obxod_1(left[i],u+1); obxod_1(right[i],u+1); end;
end;
end;
Вызов процедуры в основной программе:
for j:=1 to h do
obxod_7(1,1);
Назад
Меню
Список обходов
Слайд 29
Обход по уровням, справа налево сверху вниз
A
E
B
C
D
F
G
I
H
Выводя на
экран значения вершин бинарного дерева (см. рис.), используя обход
по уровням, справа налево сверху вниз, получим последовательность:A E B G F D C I H
Назад
Меню
Слайд 30 Процедура обхода бинарного дерева по уровням, справа налево
сверху вниз на языке Паскаль:
procedure obxod_8(i,u:integer);
begin
if i0 then
begin
if j
= u then write(key[i]:4)else begin obxod_1(right[i],u+1); obxod_1(left[i],u+1); end;
end;
end;
Вызов процедуры в основной программе:
for j:=1 to h do
obxod_8(1,1);
Назад
Меню
Список обходов
Слайд 31
Обход по уровням, слева на право снизу вверх
A
E
B
C
D
F
G
I
H
Выводя
на экран значения вершин бинарного дерева (см. рис.), используя
обход по уровням, слева на право снизу вверх, получим последовательность:H I C D F G B E A
Назад
Меню
Слайд 32 Процедура обхода бинарного дерева по уровням, слева на
право снизу вверх абсолютно идентична процедура обхода бинарного дерева
по уровням, слева на право сверху вниз, изменится только вызов данной процедуры в основной программе:for j:= h downto 1 do obxod_7(1,1);
Назад
Меню
Список обходов
Слайд 33
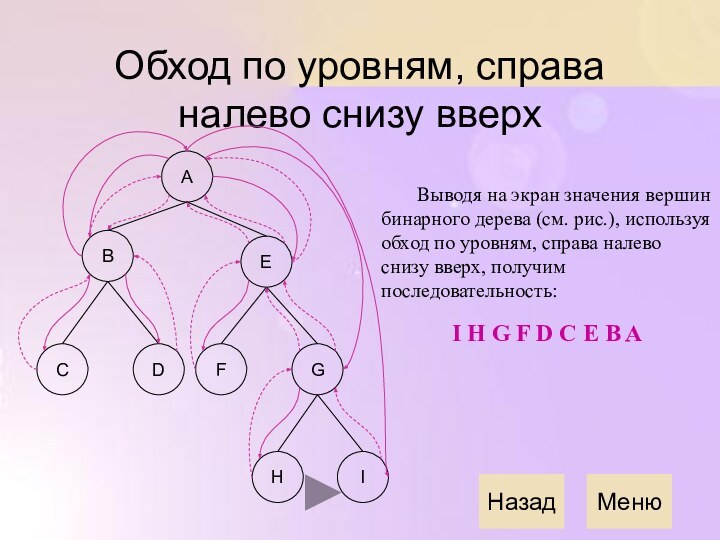
Обход по уровням, справа налево снизу вверх
A
E
B
C
D
F
G
I
H
Выводя на
экран значения вершин бинарного дерева (см. рис.), используя обход
по уровням, справа налево снизу вверх, получим последовательность:I H G F D C E B A
Назад
Меню





























