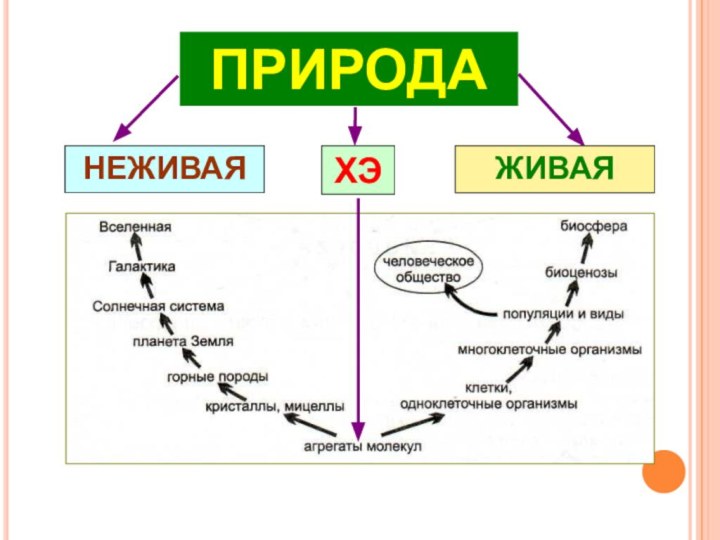
Слайд 2
Симметрия!
Я гимн тебе пою!
Тебя повсюду в мире узнаю.
Ты
в Эйфелевой башне, в малой мошке,
Ты в елочке, что
у лесной дорожки,
С тобою в дружбе и тюльпан, и роза,
И снежный рой – творение мороза.
Слайд 3
Повторить:
понятие «движение» и вспомнить основные виды движения;
понятие «многогранники»
и рассмотреть основные виды симметрии в многогранниках;
Понятие «кристаллы» и
вспомнить основные типы кристаллических решеток.
Исследовать вопрос «Симметрия в природе».
Рассмотреть различные виды симметрии в природных объектах.
Показать, что природа – это мир симметрии и основа красоты и гармонии Вселенной.
ЦЕЛИ УРОКА:
Слайд 4
Движение. Виды движения
Движение плоскости – это отображение плоскости
на себя, сохраняющее расстояния.
Виды движения:
1. Симметрия:
─
осевая,
─ центральная,
─ зеркальная.
2. Параллельный перенос.
3. Поворот.
Слайд 5
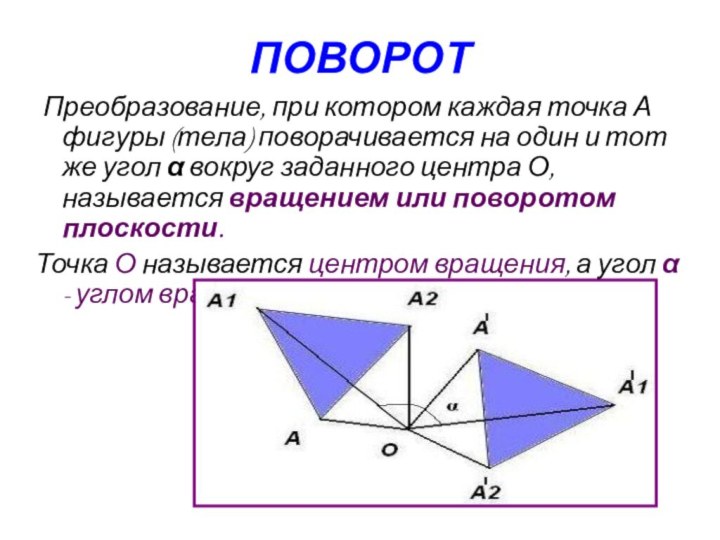
ПОВОРОТ
Преобразование, при котором каждая точка А фигуры
(тела) поворачивается на один и тот же угол α
вокруг заданного центра О, называется вращением или поворотом плоскости.
Точка О называется центром вращения, а угол α - углом вращения.
Слайд 6
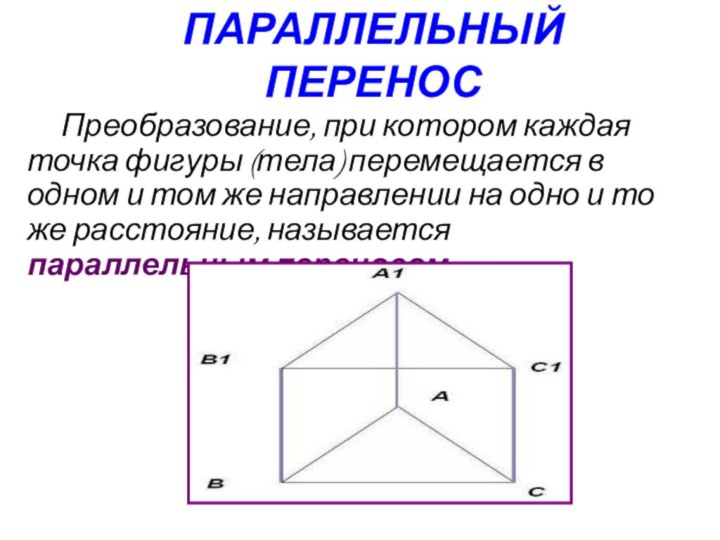
ПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
Преобразование, при котором каждая точка фигуры
(тела) перемещается в одном и том же направлении на
одно и то же расстояние, называется параллельным переносом.
Слайд 7
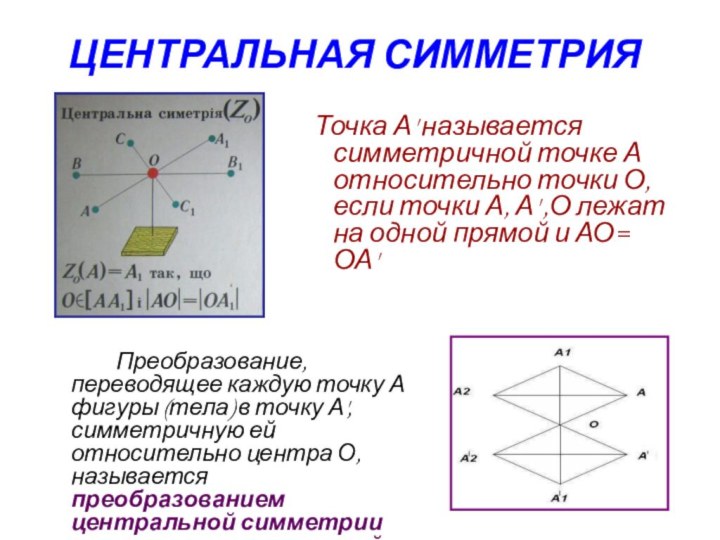
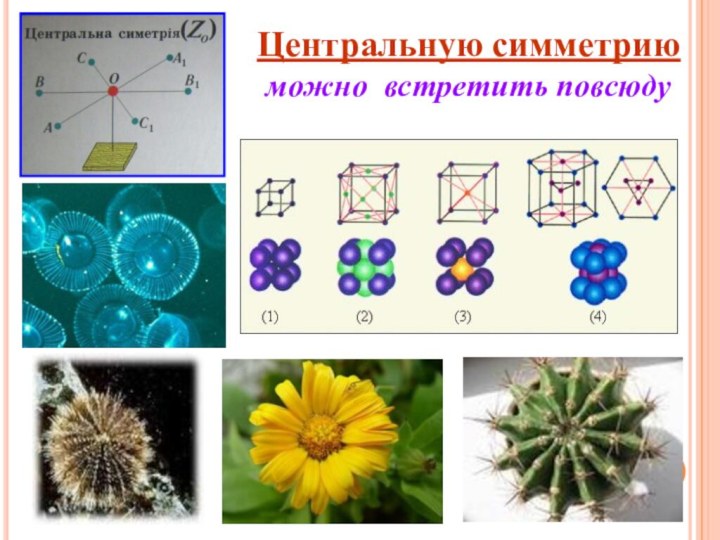
ЦЕНТРАЛЬНАЯ СИММЕТРИЯ
Преобразование, переводящее каждую точку А фигуры (тела)
в точку А', симметричную ей относительно центра О, называется
преобразованием центральной симметрии или просто центральной симметрией.
Точка А' называется симметричной точке А относительно точки О, если точки А, А' ,О лежат на одной прямой и АО= ОА'
Слайд 8
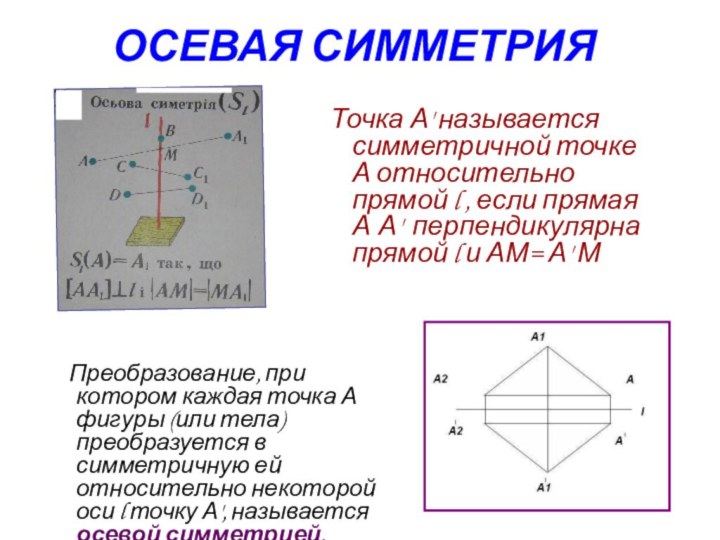
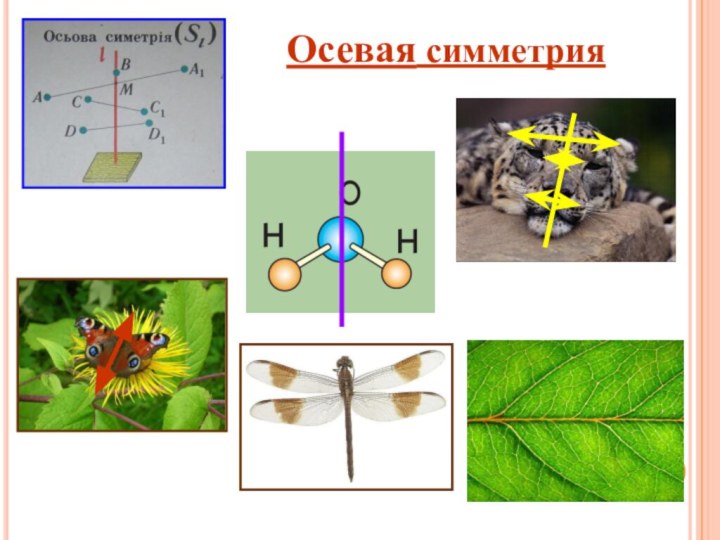
ОСЕВАЯ СИММЕТРИЯ
Преобразование, при котором каждая точка
А фигуры (или тела) преобразуется в симметричную ей относительно
некоторой оси l точку А', называется осевой симметрией.
Точка А' называется симметричной точке А относительно прямой l , если прямая А А' перпендикулярна прямой l и АМ= А' М
Слайд 9
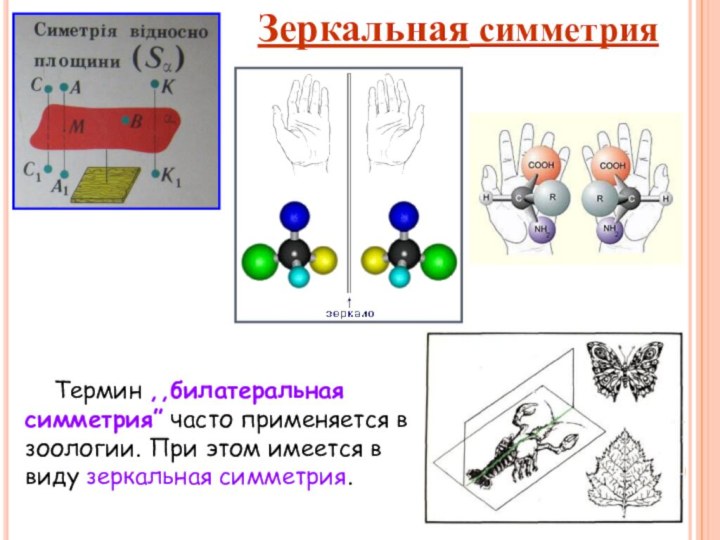
ЗЕРКАЛЬНАЯ СИММЕТРИЯ
Если преобразование симметрии
относительно плоскости переводит фигуру (тело) в себя, то фигура
называется симметричной относительно плоскости, а данная плоскость – плоскостью симметрии этой фигуры.
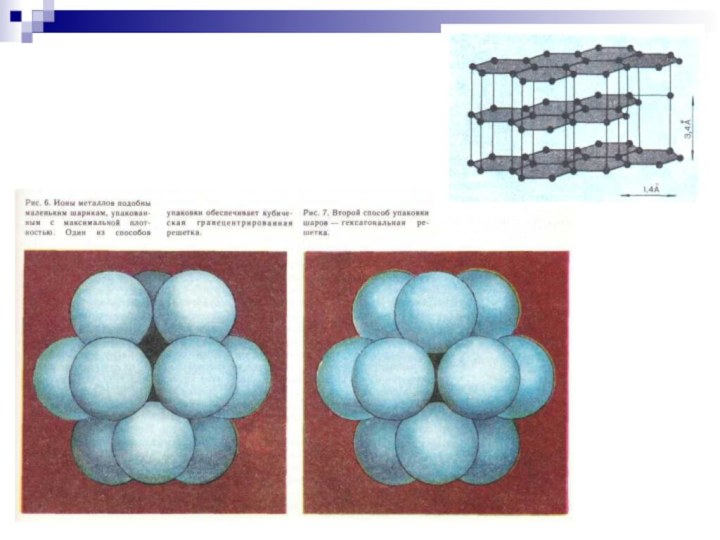
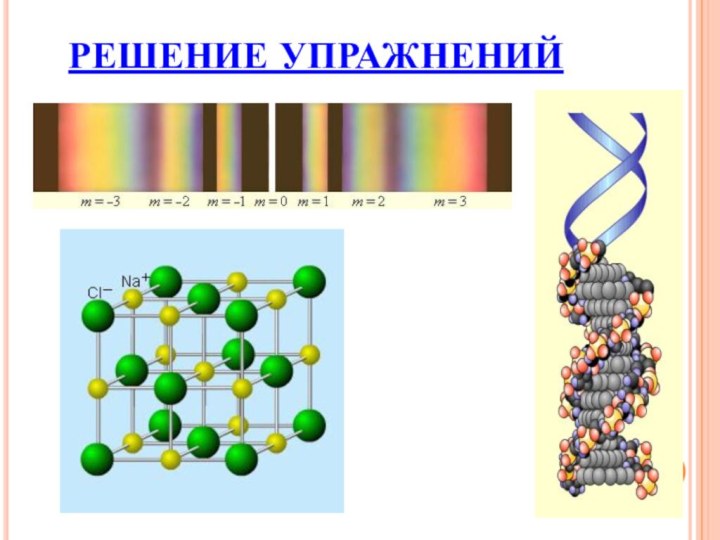
Слайд 13
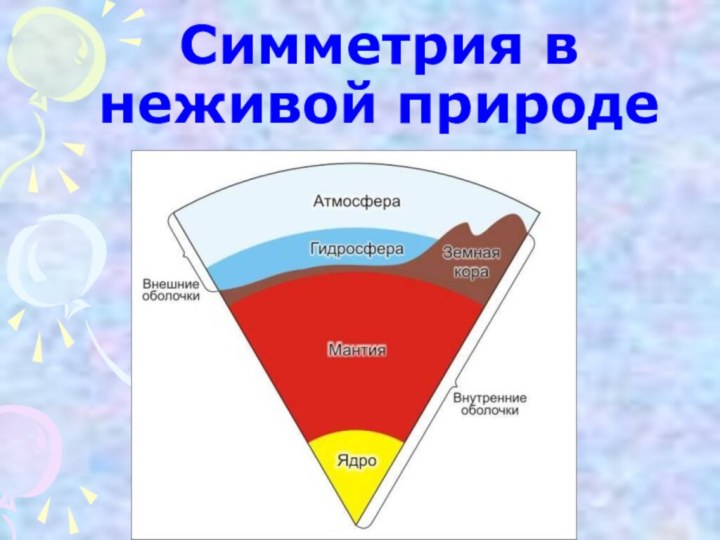
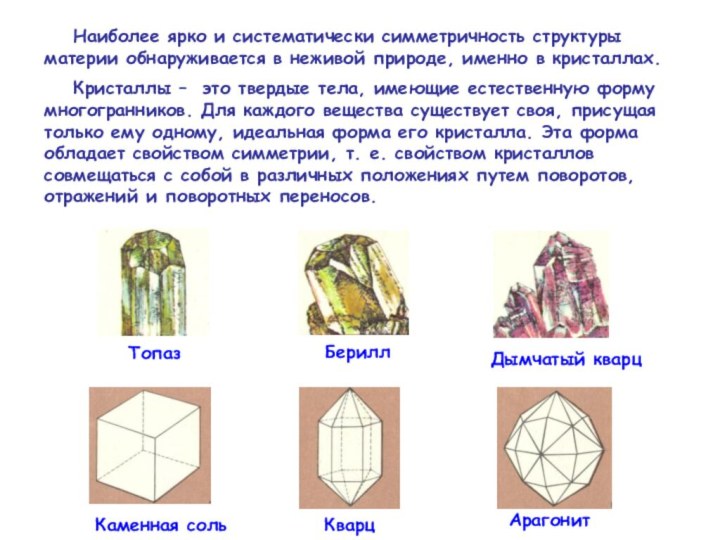
Наиболее ярко и систематически симметричность структуры материи обнаруживается
в неживой природе, именно в кристаллах.
Кристаллы – это
твердые тела, имеющие естественную форму многогранников. Для каждого вещества существует своя, присущая только ему одному, идеальная форма его кристалла. Эта форма обладает свойством симметрии, т. е. свойством кристаллов совмещаться с собой в различных положениях путем поворотов, отражений и поворотных переносов.
Слайд 14
ПОВОРОТНАЯ СИММЕТРИЯ (центрально-симметричная).
Говорят, что объект обладает поворотной
симметрией, если он совмещается сам с собой при повороте
на угол n, где n может равняться 2, 3, 4 и т.д. до бесконечности. Ось симметрии называется ось осью n-го порядка.
Слайд 15
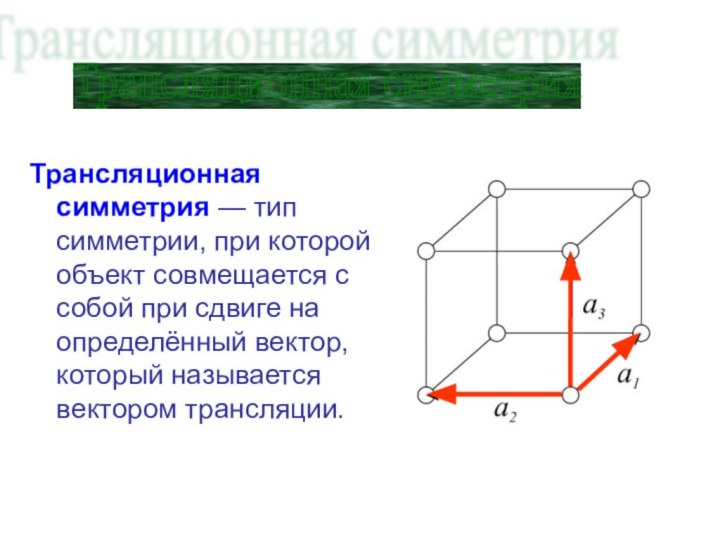
Трансляционная симметрия — тип симметрии, при которой объект
совмещается с собой при сдвиге на определённый вектор, который
называется вектором трансляции.
Трансляционная симметрия
Слайд 16
Трансляционная и поворотная симметрии не всегда
уживаются одна с другой. При наличии трансляционной симметрии возможны
только оси симметрии, отвечающие поворотам на 180, 120, 90 и 60о. Эти оси имеют порядок 2, 3, 4 и 6. Строго математически доказано, что отмеченные порядки осей в том или ином сочетании для кристаллов единственно возможны. Других порядков осей симметрии в классической кристаллографии не существует. Например, не может быть оси симметрии, соответствующей повороту на угол 72о
Периодические сетки с различными типами осей симметрии:
1 и 2 – прямоугольники и параллелограммы с осью 2-го порядка;
3 – правильные треугольники с осью 3-го порядка;
4 – квадраты с осью 4-го порядка;
5 – правильные шестиугольники с осью 6-го порядка
Слайд 18
История правильных многогранников уходит в глубокую древность. Начиная
с 7 века до нашей эры в Древней Греции
создаются философские школы, в которых происходит постепенный переход от практической к философской геометрии. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.
Историческая справка
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора. Отличительным знаком
пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник. Пентаграмме присваивалось способность защищать человека от злых духов.
Слайд 19
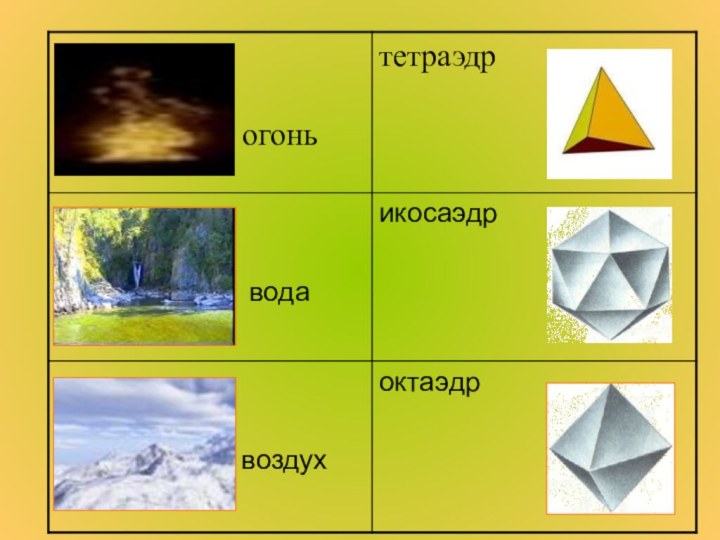
Пифагорейцы, а затем Платон полагали, что материя состоит
из четырех основных элементов: огня, земли, воздуха и воды.
Существование
пяти правильных многогранников они относили к строению материи и Вселенной.
Согласно этому мнению, атомы основных элементов должны иметь форму различных Платоновых тел:
Слайд 21
Все использовали в своих философских теориях
правильные многогранники.
Дальнейшее развитие математики связано с именами
Платона,
Евклида, Архимеда, Кеплера
Слайд 22
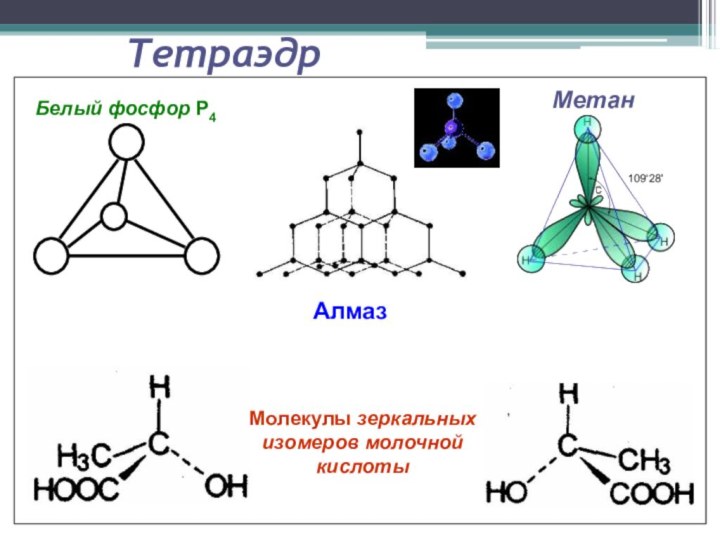
Тетраэдр
(от греческого tetra – четыре и
hedra – грань) - правильный многогранник, составленный из 4
равносторонних треугольников.
Тетраэдр имеет три оси симметрии, которые проходят через середины скрещивающихся рёбер.
Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.
Слайд 23
Тетраэдр
Белый фосфор Р4
Метан
Молекулы зеркальных изомеров молочной кислоты
Алмаз
Слайд 24
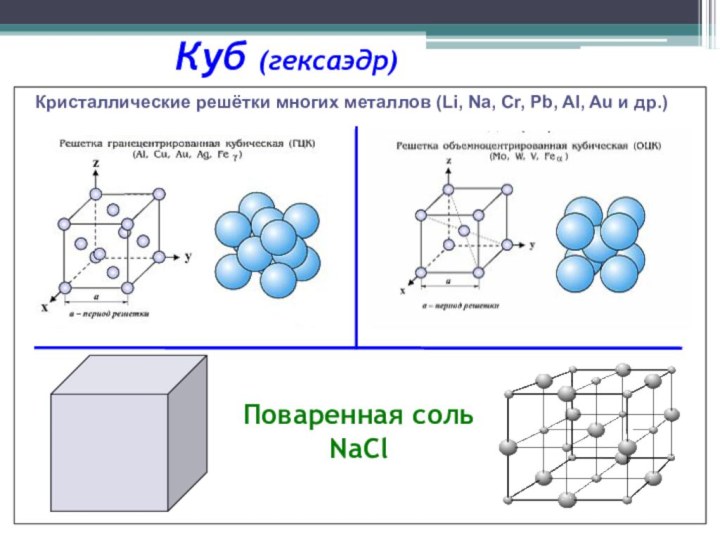
Куб (гексаэдр)
(от греческого
hex — шесть и hedra — грань) - правильный
многогранник, составленный из 6 квадратов.
Центром симметрии куба является точка пересечения его диагоналей. Через центр симметрии проходят 9 осей симметрии.
Плоскостей симметрии у куба также 9 и проходят они либо через противоположные ребра ( таковых плоскостей 6), либо через середины противоположных ребер (таких - 3).
Слайд 25
Кристаллические решётки многих металлов (Li, Na, Cr,
Pb, Al, Au и др.)
Куб (гексаэдр)
Поваренная соль
NaCl
Слайд 26
Октаэдр
(от греческого okto –
восемьи hedra – грань) –правильный многогранник, составленный из 8
равносторонних треугольников.
Октаэдр обладает симметрией. Три из 9 осей симметрии октаэдра проходят через противоположные вершины, шесть - через середины ребер. Центр симметрии октаэдра - точка пересечения его осей симметрии.
Три из 9 плоскостей симметрии тетраэдра проходят через каждые 4 вершины октаэдра, лежащие в одной плоскости. Шесть плоскостей симметрии проходят через две вершины, не принадлежащие одной грани, и середины противоположных ребер.
Слайд 27
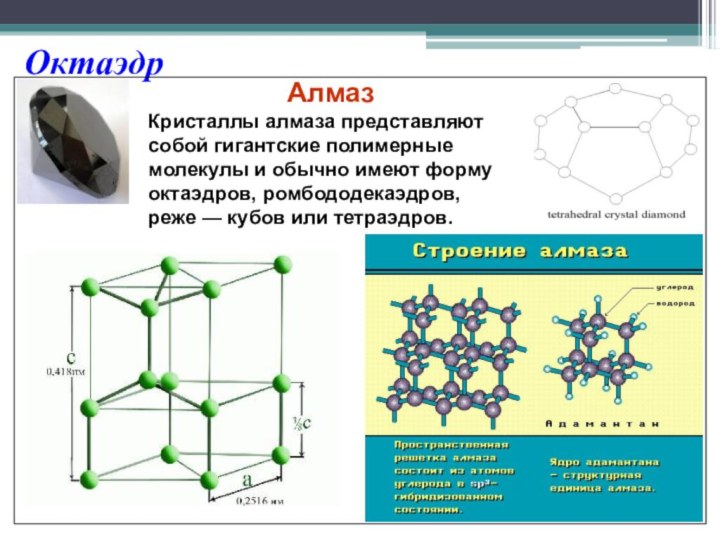
Алмаз
Кристаллы алмаза представляют собой гигантские полимерные молекулы
и обычно имеют форму октаэдров, ромбододекаэдров, реже — кубов
или тетраэдров.
Октаэдр
Слайд 28
Додекаэдр
(от греческого dodeka –
двенадцать и hedra – грань) – это правильный многогранник,
составленный из двенадцати равносторонних пятиугольников.
Додекаэдр имеет 15 плоскостей симметрии. Любая из плоскостей симметрии проходит в каждой грани через вершину и середину противоположного ребра.
Додекаэдр имеет центр симметрии и 15 осей симметрии. Каждая из осей проходит через середины противолежащих параллельных ребер.
Слайд 29
Вирус полиомиелита
Додекаэдр
Фуллерены
Слайд 30
Икосаэдр
(от греческого ico —
шесть и hedra — грань) правильный
выпуклый многогранник, составленный из
20 правильных треугольников.
Плоскостей симметрии также 15. Плоскости симметрии проходят через четыре вершины, лежащие в одной плоскости, и середины противолежащих параллельных ребер.
Правильный икосаэдр имеет 15 осей симметрии, каждая из которых проходит через середины противоположных параллельных ребер.
Слайд 31
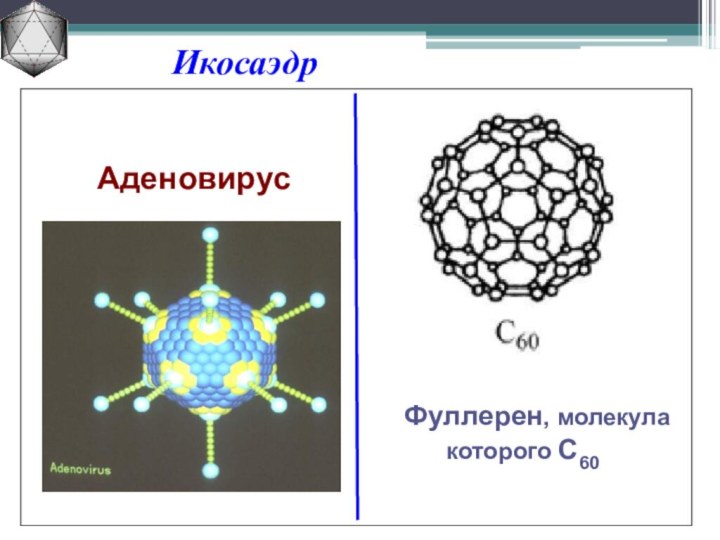
Икосаэдр
Фуллерен, молекула которого С60
Аденовирус
Слайд 32
Одной из разновидностей кристалла является снежинка. Снежинка -
это маленький кристалл замершей воды. Форма снежинок может быть
разнообразной, но все они обладают симметрией – поворотной симметрией 6-го порядка, и зеркальной симметрией.
Слайд 33
В XX веке предпринимались неоднократные попытки
расширить традиционные схемы кристаллического порядка симметрии и ввести понятие
не совсем "правильных" или "почти" периодических кристаллов. Чтобы понять возникавшие при этом трудности рассмотрим двухмерную решетку с симметрией 5-го порядка.
Осью симметрии 5-го порядка обладают правильные пятиугольники.
Их нельзя на плоскости подогнать друг к другу плотно, без зазоров.
Остающееся свободное пространство называют несогласованием .
Именно несогласование и оказывается камнем преткновения для сущест-
вования в кристаллах осей симметрии 5-го, 7-го и более высоких
порядков.
Слайд 34
Некоторое время спустя было обнаружено и синтезировано
множество аналогичных структур названных квазикристаллами. Квази… (лат. quasi -
как будто, будто бы) - приставка при различных словах, соответствующая по значению словам «мнимый», «ненастоящий», «якобы».К настоящему времени в большинстве синтезированных квазикристаллов обнаружены оси симметрии 5-го, 7-го, 8-го, 10-го, 12-го и еще более высоких порядков, запрещенные для идеальных кристаллов.
Считалось, что в неживой природе симметрии 5-го порядка не реализуются. Каково же было удивление кристаллографов и физиков, когда неожиданно в печати появилась работа группы Д. Шехтмана об открытии сплава алюминия с марганцем с необычными свойствами. Он имел структуру похожую на кристалл, но им не являлся, так как обладал вращательной симметрией 5-го порядка.
Слайд 35
Квазикристаллы
До XX века были возможны кристаллы
с симметрией 2,3,4 и 6 порядков(360◦/2, 360◦/3 и т.д.).
Эти значения были возможны только в трансляционной симметрии (Трансляционная симметрия - повторяемость объекта в пространстве через определенное расстояние вдоль прямой, называемой осью трансляции). Многие учёные пытались доказать существование «почти» правильных кристаллов, т.е. кристаллов с поворотной симметрией 5-го, 7-го и т.д. порядков (Поворотная симметрия - свойство кристалла совмещаться с самим собой при вращении на некоторый определенный угол вокруг оси симметрии ).
Этим попыткам почти не уделялось внимания, т.к. считалось, что в неживой природе такое невозможно. Но группа Д.Шехтмана смогла получить сплав Al и Mn с симметрией 5 порядка. Это была настоящая сенсация. Некоторое время спустя было обнаружено и синтезировано множество аналогичных структур, состоящих, как правило, из атомов металлов и (иногда) кремния, названных квазикристаллами.
Слайд 36
Симметрия в ботанике
анютины глазки
Слайд 37
СИММЕТРИЯ В РАСТЕНИЯХ
Ярко выраженной симметрией обладают листья, ветви,
цветы, плоды.
Зеркальная симметрия характерна для листьев, но встречается и
у цветов.
Для цветов характерна поворотная симметрия.
В многообразном мире цветов
встречаются поворотные оси
разных порядков.
Слайд 38
У цветов встречается зеркальная симметрия, однако, у них
эта симметрия чаще выступает в сочетании с поворотной и
переносной симметрией.
Интересно ,что в цветочном
мире наиболее распространена
поворотная симметрия V порядка, которая принципиально невозможна в периодических структурах неживой природы.
Слайд 39
Эта симметрия встречается у:
многих полевых цветов (колокольчик, незабудка,
герань, гвоздика, зверобой, лапчатка),
цветов плодовых деревьев (вишня, яблоня,
груша, мандарин и др.),
цветов плодово-ягодных растений (земляника, малина, калина, черёмуха, рябина, шиповник, боярышник) и др.
Слайд 40
В природе существуют тела, обладающие винтовой симметрией, т.е.
совмещением со своим первоначальным положением после поворота на определенный
угол вокруг оси дополнительным сдвигом вдоль той же оси.
Винтовая симметрия
Слайд 41
Винтовая симметрия наблюдается в расположении листьев на стеблях
большинства растений. Располагаясь винтом по стеблю, листья как бы
раскидываются во все стороны и не заслоняют друг друга от света, крайне необходимого для жизни растений. Это интересное ботаническое явление носит название филлотаксиса (буквально ,, устроение листа”).
Слайд 42
Другим проявлением филлотаксиса оказывается устройство соцветие подсолнечника
или чешуи еловой шишки, в которой чешуйки располагаются в
виде спиралей и винтовых линий. Такое расположение особенно чётко видно у ананаса, имеющего более или менее 6-угольные ячейки, которые образуют ряды, идущие в различных направлениях.
Слайд 43
Для растений характерна симметрия конуса, которая хорошо
видна на примере фактически любого дерева.
Дерево имеет вертикальную поворотную
ось (ось конуса) и вертикальные плоскости симметрии.
Вертикальная ориентация оси конуса, характеризующего симметрию дерева, определяется направлением силы тяжести.
Слайд 45
Симметричность относительно поворотов на произвольный угол вокруг какой-либо
оси.
В нее входят так же лучевая и радиальная симметрии
Аксиальная
симметрия
Слайд 46
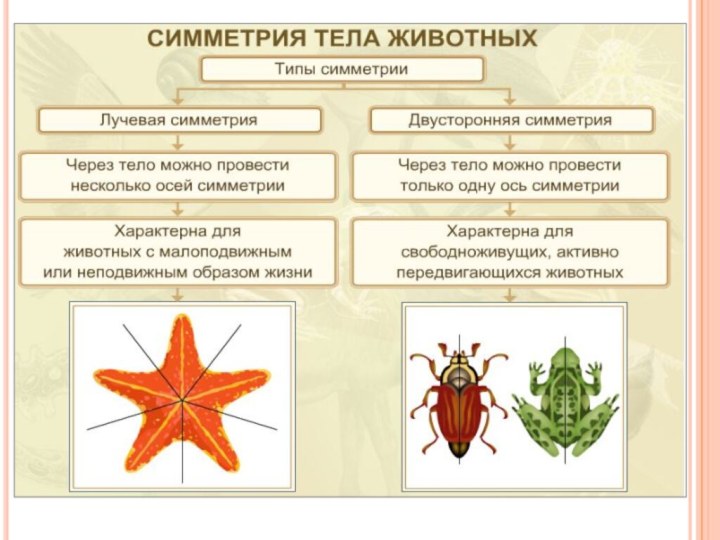
Лучевая симметрия - особый порядок расположения частей тела
животного по отношению к оси его симметрии, при котором
они расходятся от нее подобно лучам от источника света.
Лучевая симметрия
В нем можно различить главную продольную ось, вокруг которой в радиальном порядке размещения различные органы. Через тело можно провести несколько (2-4-6-8- и т.д.) плоскостей симметрии.
Слайд 47
Поворотная симметрия пятого порядка встречается и в животном
мире. Примерами могут служить морская звезда и панцирь морского
ежа.
Слайд 48
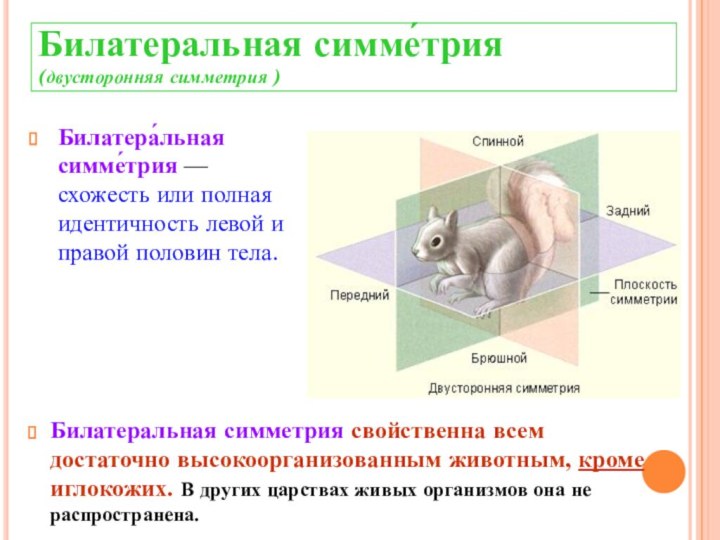
Билатеральная симме́трия
(двусторонняя симметрия )
Билатера́льная симме́трия — схожесть или
полная идентичность левой и правой половин тела.
Билатеральная симметрия
свойственна всем достаточно высокоорганизованным животным, кроме иглокожих. В других царствах живых организмов она не распространена.
Слайд 51
СИММЕТРИЯ В ПРИРОДЕ
В природе с помощью математики красота
не создаётся, как в технике и искусстве, а лишь
фиксируется, выражается.
В основе строения любой живой формы лежит принцип симметрии. Из прямого наблюдения мы можем вывести законы геометрии и почувствовать их несравненное совершенство.
Этот порядок, являющийся закономерной необходимостью, поскольку ничто в природе не служит чисто декоративным целям, помогает нам найти общую гармонию, на которой зиждется всё мироздание.
Слайд 52
Кристаллы-природные многогранники
Все камни состоят из кристаллов. Многие кристаллы
имеют удивительно красивые формы многогранников, многие из которых придумал
не человек, а природа. И создала она их в виде кристаллов.
Все кристаллы симметричны.
В каждом кристаллическом многограннике можно найти плоскости симметрии, оси и центры симметрии.
При описании кристаллических структур используют чаще всего две специфические операции симметрии трансляционную (переносную) и поворотную (вращательную).
Слайд 53
Центральную симметрию можно встретить повсюду
Слайд 55
Зеркальная симметрия
Термин ,,билатеральная симметрия” часто применяется
в зоологии. При этом имеется в виду зеркальная симметрия.
Слайд 56
Радиальная симметрия — форма симметрии, сохраняющаяся при вращении
объекта вокруг определённой точки или прямой.
Поворотная (вращательная) симметрия
Часто эта точка совпадает с центром тяжести объекта, то есть той точкой, в которой пересекается бесконечное количество осей симметрии.
Подобными объектами могут быть круг, шар, цилиндр или конус.
Слайд 57
Поворотная симметрия 5-го порядка, играющая важную роль
в квазикристаллах, наиболее ярко проявляется как бы в переходной
области между неживым и живым миром природы. Неожиданное появление золотой пропорции в структуре квазикристаллов говорит о присутствии в их симметрии живого "мотива", так как в отличие от неживых кристаллов только живой мир допускает замечательные соотношения золотой пропорции.
Напрашивается мысль о том, что внутреннее строение квазикристаллов служит своеобразным началом движения от застывших кристаллических форм к подвижным животрепещущим структурам.
Слайд 58
Мы видим, что природа проектирует любой
живой организм согласно определённой геометрической схеме, причём законы мироздания
имеют чёткое обоснование.
В своей книге ,,Этот правый, левый мир” М.Гарднер пишет: «…на Земле жизнь зародилась в сферически симметричных формах, а потом стала развиваться по двум главным линиям: образовался мир растений, обладающих симметрией конуса, и мир животных с билатеральной симметрией».
Слайд 59
Человек инстинктивно стремится к устойчивости, удобству, красоте. Поэтому
он тянется к предметам, у которых больше симметрий.
Почему
симметрия приятна для глаз? Видимо потому, что симметрия господствует в природе. С рождения человек привыкает к билатерально симметричным родным ему людям, насекомым, птицам, рыбам, животным.
Основу красоты многих форм, созданных природой, составляет симметрия.
Слайд 60
"Симметрия…- есть идея, с помощью которой
человек веками пытался объяснить порядок, красоту и совершенство"
Герман
Вейль (1885-1955)