Слайд 2
СЛУЧАЙНАЯ ВЕЛИЧИНА
Величину, которая в результате опыта принимает
только одно, зависящее от случая, числовое значение, назовем случайной
величиной.
Случайные величины обозначаются большими латинскими буквами (X, Y, Z), а их возможные числовые значения – маленькими латинскими буквами (x, y, z).
ПРИМЕРЫ:
Число выпадения герба при подбрасывании монеты
Число выпавших гербов при подбрасывании двух монет
Количество очков, выпадающих при подбрасывании игральной кости
Число родившихся мальчиков (или девочек) среди ста новорожденных.
Расстояние, которое пролетит снаряд при выстреле из орудия.
Ошибка измерителя высоты.
Температура воздуха на следующий день.
Слайд 3
Дискретная случайная величина
Случайная величина называется дискретной, если в
результате опыта она принимает числовые значения, которые можно перечислить
или поставить им в соответствие элементы счётного множества
Таким образом, дискретная случайная величина может быть как конечной, так и бесконечной.
Для описания дискретной случайной величины (ДСВ) просто перечислить её значения недостаточно. Необходимо для каждого значения найти соответствующую вероятность.
Вероятность того, что случайная величина Х примет то или иное значение а обозначают Р(Х=а).
Слайд 4
Какие из данных случайных величин будут дискретными?
Число выпадения
герба при подбрасывании монеты
Число выпавших гербов при подбрасывании двух
монет
Количество очков, выпадающих при подбрасывании игральной кости
Число родившихся мальчиков (или девочек) среди ста новорожденных.
Расстояние, которое пролетит снаряд при выстреле из орудия.
Ошибка измерителя высоты.
Температура воздуха на следующий день.
Слайд 5
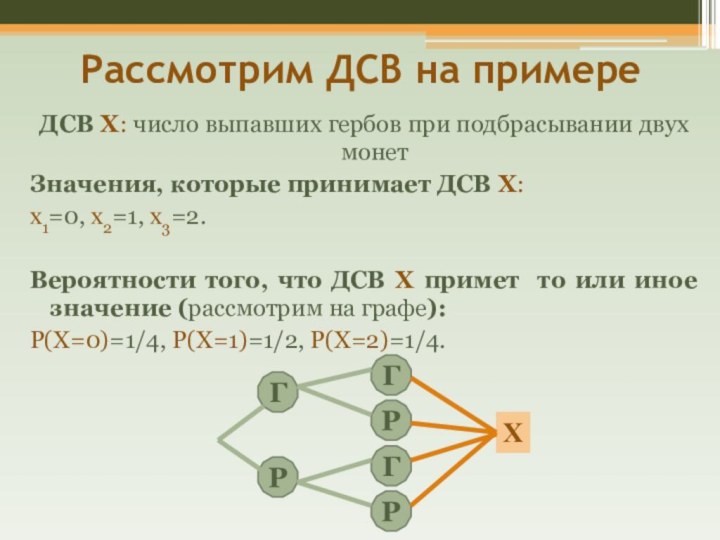
Рассмотрим ДСВ на примере
ДСВ Х: число выпавших
гербов при подбрасывании двух монет
Значения, которые принимает ДСВ Х:
х1=0, х2=1, х3=2.
Вероятности того, что ДСВ Х примет то или иное значение (рассмотрим на графе):
Р(Х=0)=1/4, Р(Х=1)=1/2, Р(Х=2)=1/4.
Г
Г
Г
Р
Р
Р
Х
Слайд 6
Закон распределения ДСВ
Соответствие между возможными значениями случайной величины
и ее вероятностями называют законом распределения случайной величины и
записывают в виде таблицы:
где в верхней строчке написаны значения случайной величины, а в нижней – под каждым xi – вероятности pi. Заметим, что события x1, x2,… xn образуют полную систему событий, поэтому сумма вероятностей в нижней строке всегда равна 1.
Для нашего примера:
Слайд 7
Многоугольник распределения
Графическим изображением закона распределения ДСВ является многоугольник
распределения - множество точек с координатами (х1; р1), (х2;
р2)… (хп; рп)…, последовательно соединенных отрезками.
Для нашего примера:
Слайд 8
Задача 1.
В стопке лежат 10 тетрадей с одинаковой
обложкой, 4 из которых в линейку, остальные – в
клетку. Саша наугад вынимает 2 тетради. Составьте закон распределения числа выбранных тетрадей в клетку
(используйте граф для нахождения вероятностей) и постройте многоугольник распределения.
Слайд 9
Задача 2.
Составьте закон распределения для суммы очков, выпадающих
при подбрасывании игральной кости (используйте граф для нахождения вероятностей)
и постройте многоугольник распределения.
Слайд 10
Задача 3*.
Стрелок производит три выстрела по мишени. Вероятность
попадания при каждом выстреле равна 0,6. Построить ряд (используйте
граф для нахождения вероятностей) и многоугольник распределения числа попаданий в мишень.
Слайд 11
Задача 4**.
Постройте граф и составьте закон распределения для
числа подбрасывания монеты до появления «герба».
Это пример бесконечной
случайной величины.
Слайд 12
Числовые характеристики ДСВ:
Математическое ожидание.
Дисперсия.
Среднеквадратическое отклонение.
Слайд 13
Математическое ожидание
Математическим ожиданием M(X) называют сумму произведений всех
возможных значений случайной величины (хi) на соответствующие вероятности (рi):
M(X) = х1·р1 + х2·р2+…+ хn·рn
Математическое ожидание – это число, которое указывает, какое среднее значение случайной величины следует ожидать в результате проведения опыта или испытания.
Слайд 14
Свойства математического ожидания
M(X) = х1·р1 + х2·р2+…+ хn·рn
1).
M(C) = C, где С – const;
2). M(C·X) =
C·M(X);
3). M(X ± Y) = M(X) ± M(Y);
4). M(X·Y) = M(X) · M(Y),
где Х и Y - независимые случайные величины.
Слайд 15
Задание:
Закон распределения случайной величины Х задан таблицей:
Найдите математическое
ожидание случайной величины Х.
M(X) = х1·р1 + х2·р2+…+ хn·рn
Слайд 16
Дисперсия
Дисперсией случайной величины Х называют математическое ожидание квадрата
ее отклонений от среднего значения:
Для вычисления:
D(X) = M(X2) - M2(X),
где M(X2) = х12·р1 + х22·р2+…+ хn2·рn
Дисперсия характеризует степень отклонения значений случайной величины от ее среднего значения. На практике дисперсия служит для оценки меры риска.
(Дисперсия всегда положительное число)
Слайд 17
Свойства дисперсии
D(X) = M(X2) - M2(X),
где
M(X2) = х12·р1 + х22·р2+…+ хn2·рn
1). D(C) = 0,
где C – const;
2). D(CּX) = CּD(X);
3). D(X ± Y) = D(X) + D(Y), если Х, Y – независимые случайные величины.
Слайд 18
Задание:
Закон распределения случайной величины Х задан таблицей:
Найдите дисперсию
случайной величины Х.
D(X) = M(X2) - M2(X),
где M(X2)
= х12·р1 + х22·р2+…+ хn2·рn
Слайд 19
Среднеквадратическое отклонение
Дисперсия имеет размерность квадрата случайной величины: если
ДСВ имеет размерность метры, то дисперсия измеряется в м2.
Для того, чтобы оценка рассеяния значений случайной величины имела размерность самой величины, вычисляют среднеквадратичное отклонение.
Положительное значение квадратного корня из дисперсии называют среднеквадратическим отклонением (или стандартным отклонением):
Слайд 20
Задание:
Закон распределения случайной величины Х задан таблицей:
Найдите среднеквадратичное
отклонение случайной величины Х.
Слайд 21
ЗАДАЧА
Прибыльность двух инвестиционных проектов Х, Y (млн. руб)
задана законами распределения:
Какой инвестиционный проект целесообразно выбрать для реализации?
Слайд 22
ЗАДАЧА 1
В партии из 10 деталей имеется 8
стандартных. Наудачу отобраны 2 детали. Составить закон распределения числа
стандартных деталей среди отобранных. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение.
Слайд 23
ЗАДАЧА 2
В коробке имеются 7 карандашей, из которых
4 красные. Из этой коробки наудачу извлекаются а). 2
карандаша, б). 3 карандаша. Определить закон распределения, математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины, равной числу не красных карандашей.
Слайд 24
ЗАДАЧА 3
Построить ряд распределения числа попаданий мячом в
корзину при трех бросках, если вероятность попадания равна 0,4.
Вычислить математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины.
Слайд 25
ЗАДАЧА 4
Определить закон распределения, математическое ожидание, дисперсию и
среднеквадратическое отклонение числа гербов при четырех подбрасываниях монеты.
Слайд 26
ЗАДАЧА 5*
Устройство состоит из трех независимо работающих элементов.
Вероятность отказа каждого элемента в одном опыте равна 0,1.
Составить закон распределения числа отказавших элементов в одном опыте. Найти математическое ожидание, дисперсию и среднеквадратическое отклонение.