работы учителей с использованием MathCAD
Рассмотреть решение систем алгебраических уравнений
с помощью MathCADЦЕЛИ РАБОТЫ
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть





































ЦЕЛИ РАБОТЫ
Для кого эта РАБОТа
Содержание работы
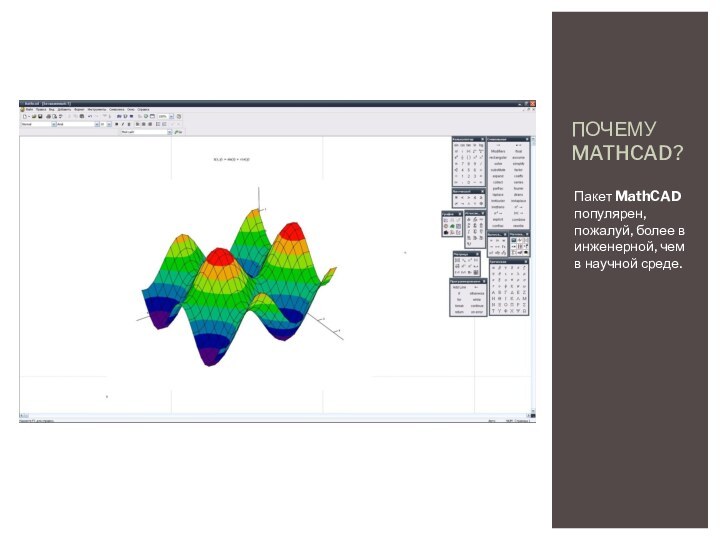
ПОЧЕМУ MATHCAD?
проводить статистические расчеты и анализ данных;
строить двумерные и трехмерные графики;
тождественные преобразования (в том числе упрощение), аналитическое решение уравнений и систем;
дифференцирование и интегрирование, аналитическое и численное;
решение дифференциальных уравнений;
И многое другое…
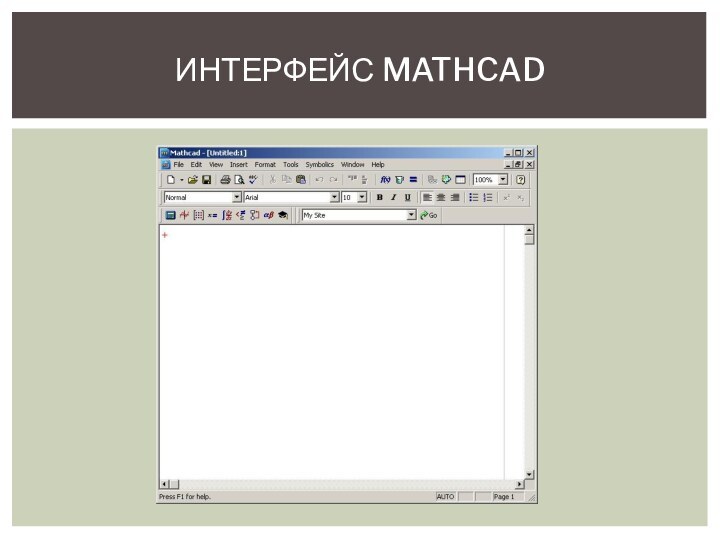
ЧТО УМЕЕТ MATHCAD?
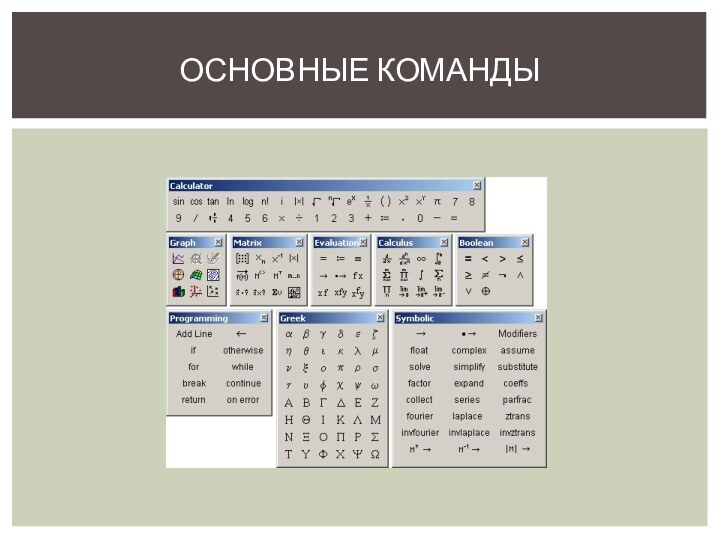
ПРАВИЛА НАБОРА КОМАНД
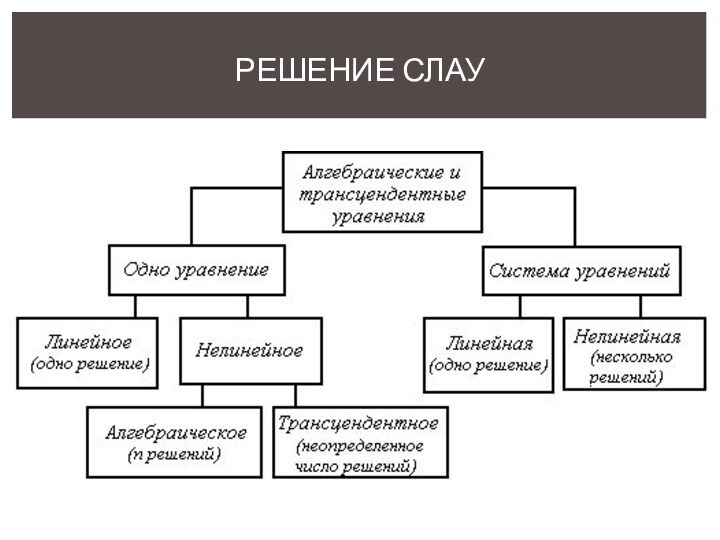
Способы решения СЛАУ
Способы решения СЛАУ
Решение СЛАУ с помощью блока Given и функции Find
Решение СЛАУ с помощью блока Given и функции Find
Решение СЛАУ матричным способом
Решение СЛАУ матричным способом
Решение СЛАУ матричным способом
Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса
Решение СЛАУ методом Гаусса
Решение СЛАУ методом КРАМЕРА