- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Применение производной
Содержание
- 2. Много из математики не остается
- 3. Цели и задачи занятия:Образовательные:Обобщения и систематизация знаний
- 4. Основные моменты урока:Устный счёт «Кто автор?» (нахождение производных)Геометрический смысл производнойФизический смысл производнойИсследование функцииПроверочная работа.Рефлексия.
- 5. Устный счёт «Кто автор слов?» (работа в
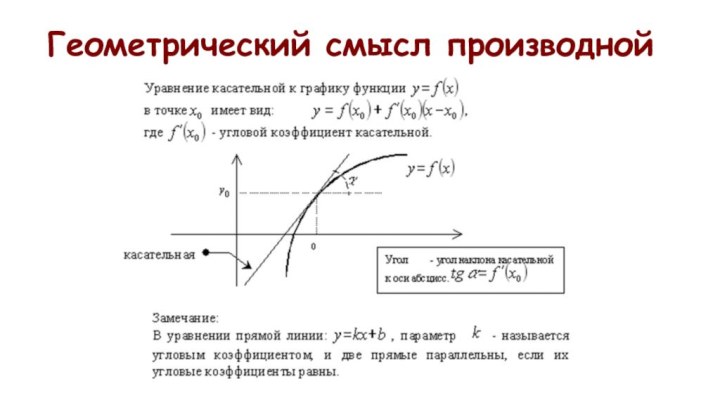
- 6. Геометрический смысл производной
- 7. Задача 1.Найдите угловой коэффициент касательной к графику
- 8. Задача 2Написать уравнение касательной к графику функции
- 9. «Практика рождается из тесного соединения физики и
- 10. Физический смысл производноймгновенная скорость(ускорение)
- 11. Задача 2Материальная точка движется прямолинейно по закону
- 12. Исследование функции Возрастание и убывание функции f(x)
- 13. Задача3 (устно)Функция у = f(x) определена на
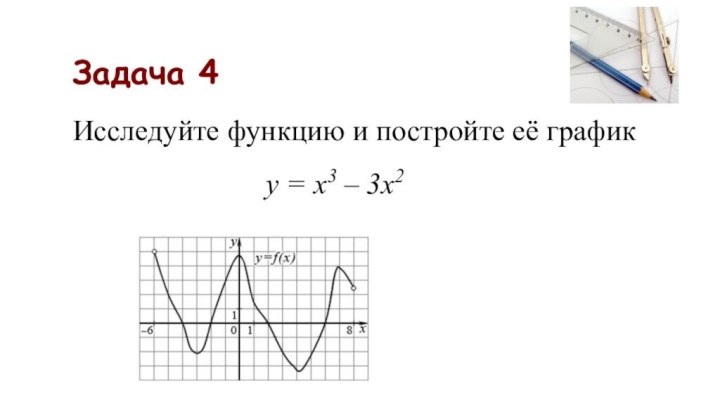
- 14. Задача 4
- 15. Наибольшее и наименьшее значения функции f(x) на
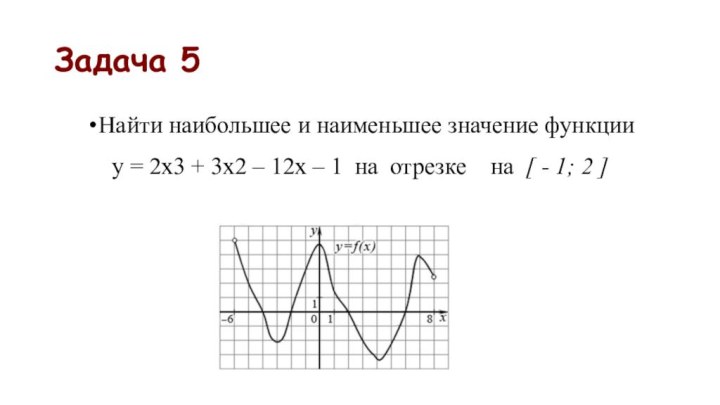
- 16. Задача 5 Найти наибольшее и наименьшее значение
- 17. Проверь себя
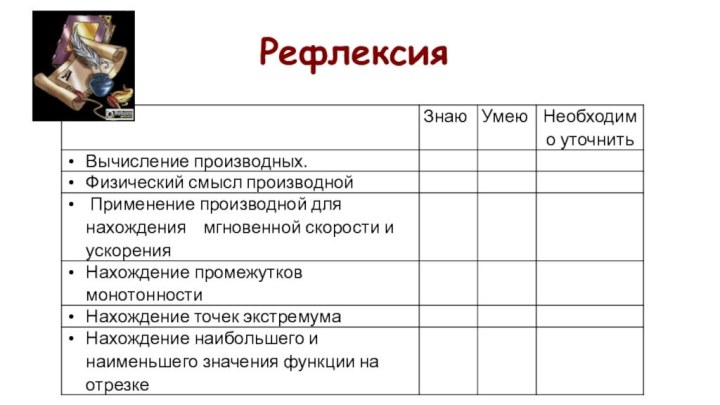
- 18. Рефлексия
- 19. «Кто с детских лет занимается математикой, тот
- 20. Скачать презентацию
- 21. Похожие презентации
Много из математики не остается в памяти, но когда поймешь ее, тогда легко при случае вспомнить забытое. М.В. Остроградский











![Применение производной Наибольшее и наименьшее значения функции f(x) на отрезке[a;b]найти значения функции на концах](/img/tmb/6/522160/e34181353e373571cd2f3ace3864c6d7-720x.jpg)



Слайд 2 Много из математики не остается в памяти, но
когда поймешь ее, тогда легко при случае вспомнить забытое.
Остроградский
Слайд 3
Цели и задачи занятия:
Образовательные:
Обобщения и систематизация знаний о
применении производной
отработка вычислительных навыков.
Развивающие:
развитие умений организовать свою деятельность,
анализировать, сопоставлять и работать в парах.Воспитательные:
формирование умений слушать других;
воспитание воли и настойчивости для достижения конечных результатов.
Слайд 4
Основные моменты урока:
Устный счёт «Кто автор?» (нахождение производных)
Геометрический
смысл производной
Физический смысл производной
Исследование функции
Проверочная работа.
Рефлексия.
Слайд 5
Устный счёт «Кто автор слов?» (работа в парах)
Сопоставьте
функцию и её производную
«..Математика - это цепь понятий: выпадет
одно звенышко –и не понятно будет дальнейшее».
Н.К. Крупская
Слайд 7
Задача 1.
Найдите угловой коэффициент касательной к графику функции
f(x) = x4 + 2x - 4 в
точке с абсциссой x0 = 1.Ответ: 6
Слайд 9 «Практика рождается из тесного соединения физики и математики»
«Что касается математики, то она интересует меня лишь постольку, поскольку я могу применить её в физике»
Эйнштейн А.
Слайд 11
Задача 2
Материальная точка движется прямолинейно по закону x(t)=2t2−48t−3,
где x — расстояние от точки отсчета в метрах,
t — время в секундах, измеренное с начала движения. В какой момент времени (в секундах) ее скорость была равна 4 м/с?Ответ: 13 сек
Слайд 12
Исследование функции
Возрастание и убывание функции f(x) и
точки экстремума
Найти производную функции
Решить уравнение
= 0 (найти критические точки)На числовой прямой отметить критические точки.
Определить знак производной в промежутках
Если >0 , то функция возрастает
если <0, то убывает.
Точка минимума точка максимума
Слайд 13
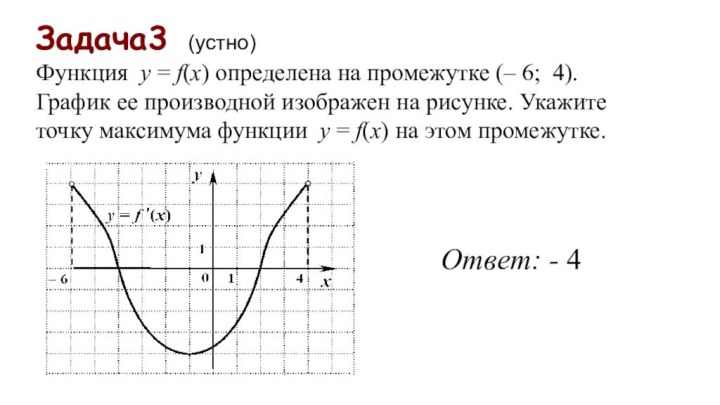
Задача3 (устно)
Функция у = f(x) определена на промежутке
(– 6; 4). График ее производной изображен на рисунке. Укажите точку
максимума функции у = f(x) на этом промежутке. Ответ: - 4
Слайд 15
Наибольшее и наименьшее значения функции f(x) на отрезке[a;b]
найти
значения функции на концах отрезка f(а) и f(b);
найти критические
точки, принадлежащие отрезку и вычислить значения функции в этих точках;из найденных значений выбрать наибольшее и наименьшее.
Слайд 16
Задача 5
Найти наибольшее и наименьшее значение функции
у = 2х3 + 3х2 – 12х – 1
на отрезке на [ - 1; 2 ]
Слайд 17
Проверь себя
1 вариант
1. Найти угловой коэффициент
касательной, проведенной к графику функции в точке х0 =22. Тело движется по прямой так, что расстояние s от начальной точки изменяется по закону у = 0,5t2 +3t + 4 (м),где t - время движения в секундах. Найдите скорость, тела через 2 с после начала движения.
3.Найдите промежутки возрастания и убывания функции, точки экстремумы функции у = х3 – 3х2 -9х -4
2 вариант
1. Найти тангенс угла наклона касательной, проведенной к графику функции f(x) =x3-3x в точке М(3;1).
2. Материальная точка движется прямолинейно по закону S(t) =18t2 – t3
Определите V(t), если t= 2 сек
3. Найдите точки экстремумы
функции у = 3х3 – 4,5х2 +4
Слайд 19 «Кто с детских лет занимается математикой, тот развивает
внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и
упорство в достижении цели».А. Маркушевич