Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Транспортная задача

Содержание

2. Пусть однородный продукт, сосредоточенный в m отправления
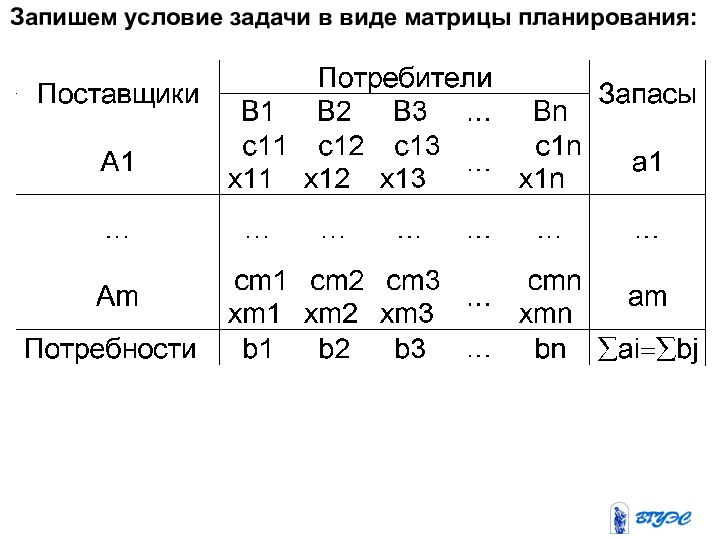
3. Запишем условие задачи в виде матрицы планирования:
4. Математическая модель задачи: т.к. от i-го поставщика
5. Стоимость всего плана выразится двойной суммой:
6. Систему ограничений получаем из следующих условий задачи:1.)
9. Построение первоначального опорного плана.
10. При решении задач ЛП итерационный процесс по описанию оптимального плана начинают с определения опорного плана.
11. Система ограничений транспортной задачи содержит mn неизвестных и m+n уравнений.
13. Клетки в таблице матрицы планирования, в которых
14. Опорность плана заключается в его ацикличности (это
15. Циклом называется набор клеток, в котором две
16. Построение циклов начинают с какой-либо занятой клетки
17. Клетки, в которых происходит поворот под прямым углом, определяют вершины цикла.
18. Если план транспортной задачи содержит более m+n-1
19. Если к занятым клеткам, определяющим опорный невырожденный
20. Скачать презентацию
21. Похожие презентации

Пусть однородный продукт, сосредоточенный в m отправления в количествах единиц, необходимо доставить в каждый из n пунктов назначения в количествах

Кафедра математики и моделированияСтарший преподаватель Е.Г. ГусевКурс «Высшая математика»Лекция 18. Тема: Транспортная

Запишем условие задачи в виде матрицы планирования:

Математическая модель задачи: т.к. от i-го поставщика к j-му потребителю запланировано к

Стоимость всего плана выразится двойной суммой:

Систему ограничений получаем из следующих условий задачи:1.) Все грузы должны быть вывезены,

Построение первоначального опорного плана.

При решении задач ЛП итерационный процесс по описанию оптимального плана начинают с определения опорного плана.

Система ограничений транспортной задачи содержит mn неизвестных и m+n уравнений.

Клетки в таблице матрицы планирования, в которых находятся отличные от 0 перевозки,

Опорность плана заключается в его ацикличности (это ситуация, при которой нельзя построить

Циклом называется набор клеток, в котором две и только две соседние клетки

Построение циклов начинают с какой-либо занятой клетки и переходят по столбцу (строке)

Клетки, в которых происходит поворот под прямым углом, определяют вершины цикла.

Если план транспортной задачи содержит более m+n-1 занятых клеток, он не является

Если к занятым клеткам, определяющим опорный невырожденный план, а значит и цикличный,

Вопросы:1)При каких условиях транспортная задача имеет решение?2)Что такое цикл?

Слайды презентации

Слайд 2 Пусть однородный продукт, сосредоточенный в m отправления в

количествах

единиц, необходимо доставить в каждый из n пунктов назначения в количествах единиц. Стоимость перевозки единицы продукта из i-го (i= ) пункта отправления в j-й (j= ) пункт назначения равна и известна для всех компаний (i; j). Пусть – количество продукта, перевозимого по маршруту (i; j). Задача - определение таких величин для всех маршрутов (i; j), при которых суммарная стоимость перевозок минимальна.

Слайд 3 Запишем условие задачи в виде матрицы планирования:

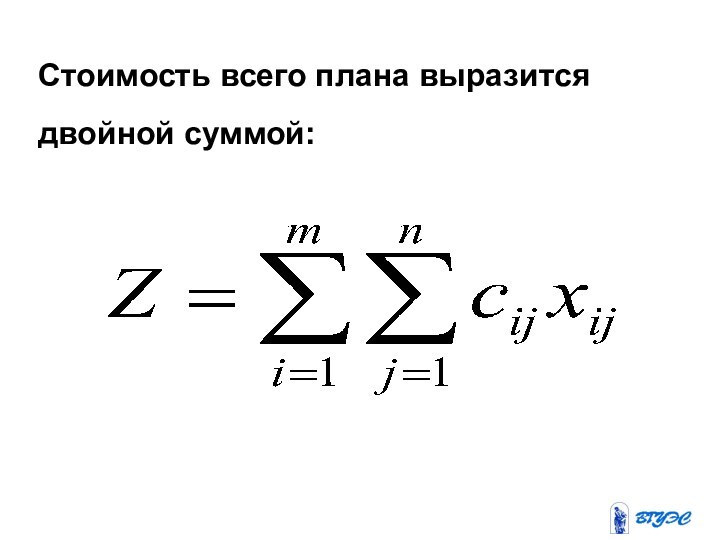
Слайд 4 Математическая модель задачи: т.к. от i-го поставщика к

Математическая модель задачи: т.к. от i-го поставщика к j-му потребителю запланировано

j-му потребителю запланировано к перевозке ед.груза, то

стоимость перевозки составит .

Слайд 5
Стоимость всего плана выразится двойной суммой:

Слайд 6 Систему ограничений получаем из следующих условий задачи:
1.) Все

Систему ограничений получаем из следующих условий задачи:1.) Все грузы должны быть

грузы должны быть вывезены, т.е.
2.) Все

потребности должны быть удовлетворены, т.е.

Слайд 7

Слайд 8

Слайд 9 Построение первоначального опорного плана.

Слайд 10 При решении задач ЛП итерационный процесс по описанию

оптимального плана начинают с определения опорного плана.

Слайд 11 Система ограничений транспортной задачи содержит mn неизвестных и

m+n уравнений.

Слайд 12

Слайд 13 Клетки в таблице матрицы планирования, в которых находятся

Клетки в таблице матрицы планирования, в которых находятся отличные от 0

отличные от 0 перевозки, называются занятыми, остальные незанятыми. Занятые

клетки соответствуют базисным неизвестным и для невырожденного опорного плана их должно быть m+n-1.

Слайд 14 Опорность плана заключается в его ацикличности (это ситуация,

Опорность плана заключается в его ацикличности (это ситуация, при которой нельзя

при которой нельзя построить замкнутый многоугольник или цикл, все

вершины которого будут лежать в занятых клетках).

Слайд 15 Циклом называется набор клеток, в котором две и

Циклом называется набор клеток, в котором две и только две соседние

только две соседние клетки расположены в одном столбце или

в одной строке таблице, причем последняя клетка находится в той же строке или столбце, что и первая.

Слайд 16 Построение циклов начинают с какой-либо занятой клетки и

Построение циклов начинают с какой-либо занятой клетки и переходят по столбцу

переходят по столбцу (строке) к другой занятой клетке, в

которой делают поворот под прямым углом и движутся по строке (столбцу) к следующей занятой клетке и т.д., пытаясь возвратиться к первоначальной клетке.