Презентация на тему Методы решения тригонометрических уравнений

в который ты не усвоил ничего нового и ничего

Я. А. Коменский

1
arcsin (- 1/2 )
arccos (- √3/2)
arctg √3

π/3

области значений функции
3. Исследование функции на четность.
4.. Исследование

является множество
всех действительных чисел ( R

2. Областью значений) - [ - 1; 1 ].

3. Функция у = sin α нечетная, т.к. sin (- α) = - sin α

4. Функция периодическая, с главным периодом 2π

sint = а, где | а |≤ 1

1)sint=0
t = 0+πk‚ kЄZ

2)sint=1
t = π/2+2πk‚ kЄZ

3)sint = - 1
t = - π/2+2πk‚ kЄZ

является множество
всех действительных чисел ( R

2. Областью изменений (Областью значений) - [ - 1; 1 ]

3. Функция у = cos α четная, т.к. cos (- α) = cos α

4. Функция периодическая, с главным периодом 2π.

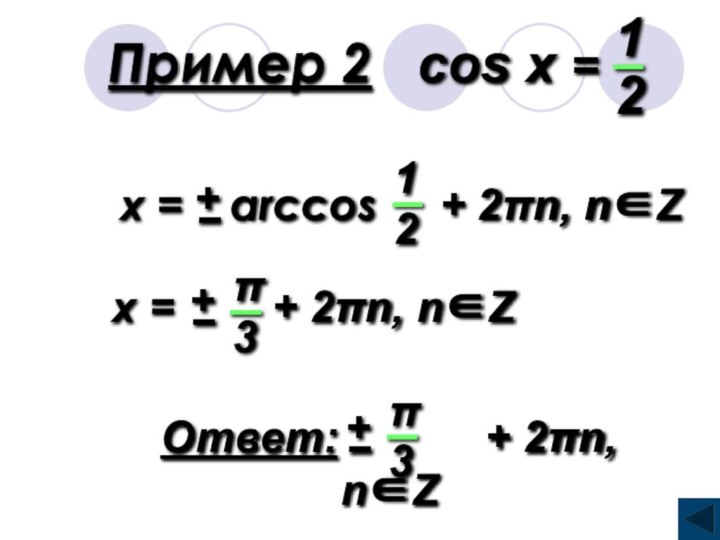
cost = а , где |а| ≤ 1

1)cost=0
t = π/2+πk‚ kЄZ

2)cost=1
t = 0+2πk‚ kЄZ

3)cost = -1
t = π+2πk‚ kЄZ

является множество (- π/2; π/2)

2. Областью значений R.
3.Функция у

4. Функция периодическая, с главным периодом π.

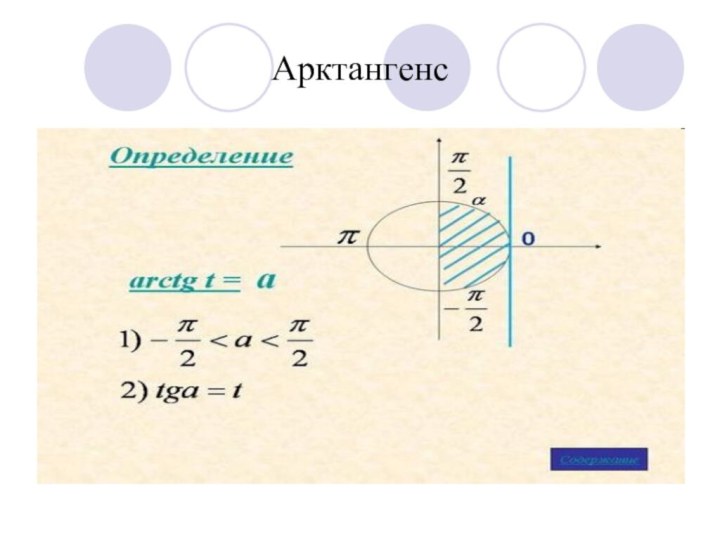
tgt = а, аЄR

t = arctg а + πk‚ kЄZ

является множество (πn; π + πn)

2. Областью значений

3. Функция у = ctg x нечетная, т.к. ctg (- α) = - ctg α

4. Функция периодическая, с главным периодом π.

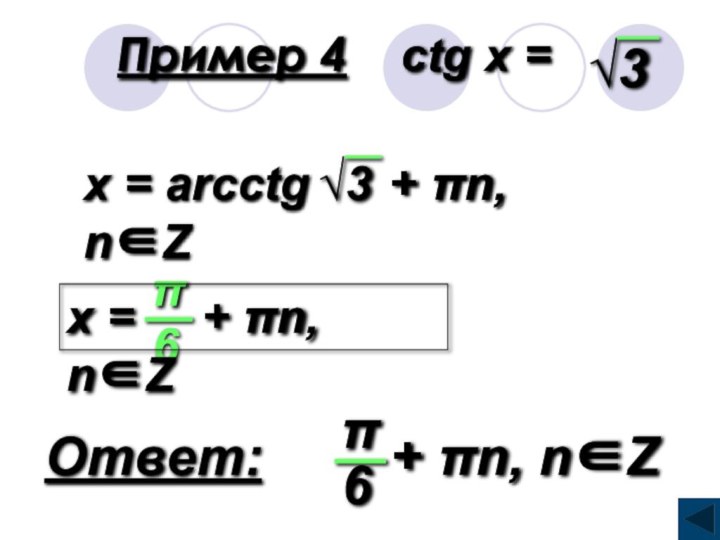
ctgt = а, аЄR

t = arcctg а + πk‚ kЄZ

= −
Пример 2Пример 2. cos x =

= arctg (− 1) + πn, n∈Z
x = −

a∙sin²x + b∙sinx + c=0

2.Однородные
1)Первой степени:
a∙sinx +

2)Второй степени:
a∙sin²x + b∙sinx∙cosx + c∙cos²x = 0
Разделим обе части на cos²x.

помощью тригонометрических формул:
Формул сложения
Формул приведения
Формул двойного аргумента

3 sin x+ 5 cos x = 0
2) 5

На «3»
1) cos x+ 3 sin x = 0
2) 6 sin2 х - 5 sinх cos х + cos2х =0
На «4»
1) 2 sin2 x – sin x cosx =0
2) 4 sin2 х - 2sinх cos х – 4 cos2х =1
На «5»
1) 2 sin x - 3 cos x = 4
2) 2 sin2 х - 2sin 2х +1 =0

то чего мы не знаем, - бесконечно». Пьер