Презентация на тему Ох уж эти дроби ( 5 класс)

теме «Дроби»
Задачи:
собрать дополнительный теоретический материал по теме «Дроби»
сделать

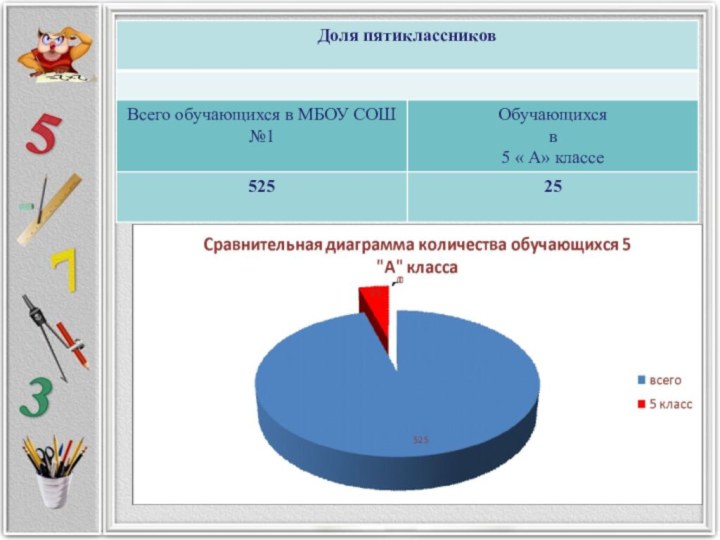
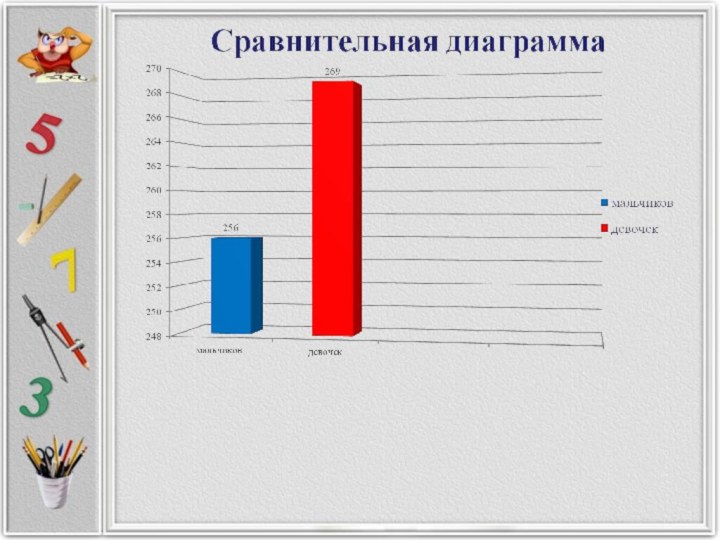
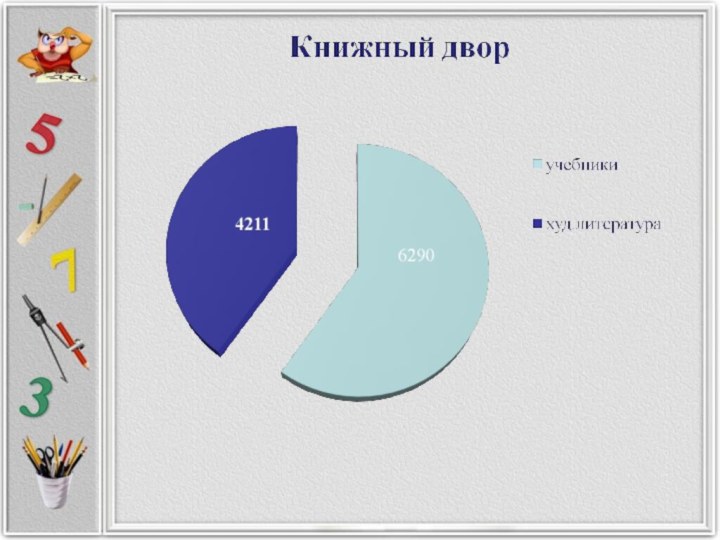
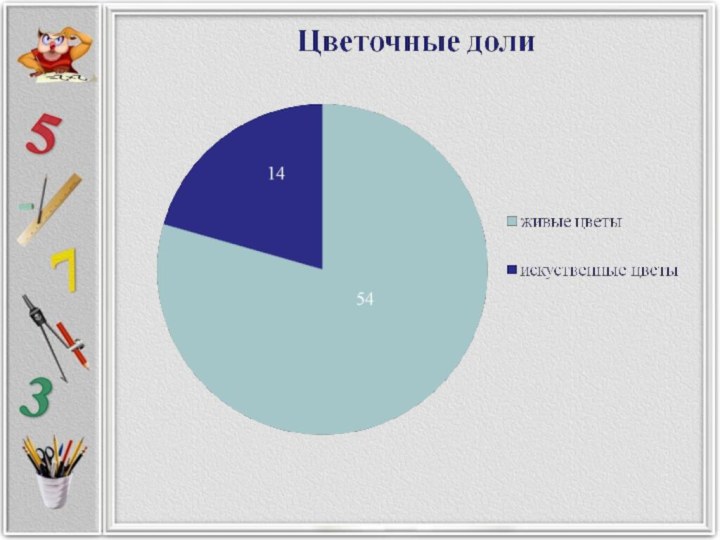
подборку нестандартных задач с дробями
найти незримую явно связь окружающего нас мира с миром дробных чисел (составить таблицы, диаграммы)
создать электронную презентацию по нашему проекту
продемонстрировать другим учащимся, что мир дробей может быть очень увлекательным
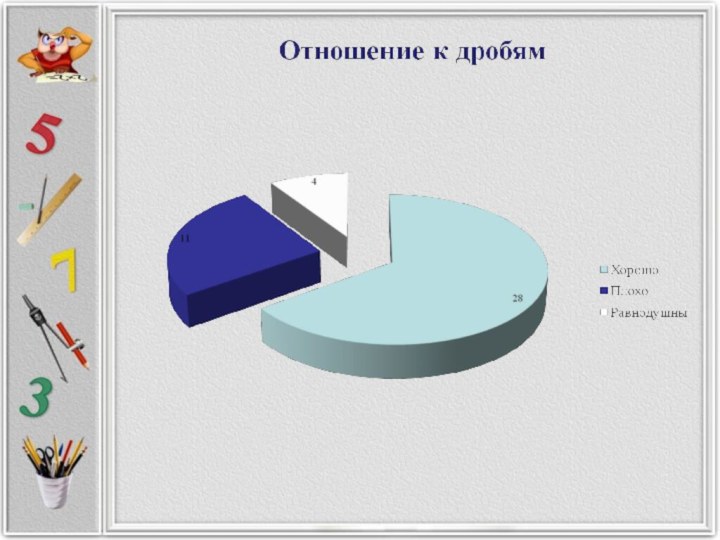
провести опрос учащихся с целью определения степени эффективности нашей работы
дать свои рекомендации учителям математики по повышению заинтересованности учащихся при изучении дробей
Тип проекта: практико-ориентированный.
Виды деятельности: творческий, информационный, прикладной.
Применяемые умения: -проектные (организационные, информационные, поисковые, коммуникативные, презентационные, оценочные); -предметные (математические).
База выполнения: школьная.
Формы обучения: групповая и индивидуальная.
Продолжительность выполнения: средняя продолжительность – один месяц.
Средства обучения: печатные, наглядные, компьютерные презентации.
Формы продуктов деятельности: электронная презентация

Курьезное и серьёзное о числах
3. Подготовили презентации « Исторические

сведения о дробях»
4. Сделали подборку интересных , занимательных , необычных задач :
« К ужину – 3 поджаренных ломтика» , « Продажа яблок» ,
« Число 666» , « Крестьяне и картофель», «Недоумение крестьянок», «Делёж верблюдов»
5.Подготовили интересный материал « Как решать задачу».

это наука о хитроумных операциях, производимых по специально разработанным

правилам над специально придуманными понятиями. Ясно, что особенно важная роль при этом отводится придумыванию новых понятий. Запас интересных теорем в математике быстро исчерпался бы, если бы их приходилось формулировать лишь при помощи понятий, содержащихся в аксиомах. Ю. П. Вигнер
Чистая математика - это такой предмет, где мы знаем, о чем мы говорим, и не знаем, истинно ли то, о чем мы говорим. Бертран Рассел
Я не мог понять содержания вашей статьи, так как она не была оживлена иксами и игреками. У. Томсон (лорд Кельвин)
Математика представляет собой собрание выводов, которые могут быть применены к чему угодно. Бертран Рассел
Из дома реальности легко забрести в лес математики, но лишь немногие способны вернуться обратно.(Хуго Штейнгаус)
В каждой естественной науке заключено столько истины, сколько в ней математики. (Иммануил Кант)
Подобно тому как все искусства тяготеют к музыке, все науки стремятся к математике. (Джордж Сантаяна)
Математика может открыть определенную последовательность даже в хаосе. (Гертруда Стайн)
Математики похожи на влюбленных - достаточно согласиться с простейшим утверждением математика, как он выведет следствие, с которым вновь придется согласиться, а из этого следствия - еще одно. (Бернар Ле Бовье де Фонтенель)

счета предметов употреблялись лишь два числительных: один и два.

В процессе дальнейшего расширения системы счисления привлекались части человеческого тела и в первую очередь пальцы, а если не хватало такого рода «цифр», то еще палочки, камешки и другие вещи.
Н. Н. Миклухо-Маклай в своей книге «Путешествия» рассказывает о забавном способе счета, применявшемся туземцами Новой Гвинеи:
«Излюбленный способ счета состоит в том, что папуас загибает один за другим пальцы руки, причем издает определенный звук, например, «бе, бе, бе» ... Досчитав до пяти, он говорит «ибон-бе» (рука). Затем он загибает пальцы другой руки, снова повторяет «бе, бе» ..., пока не доходит до «ибон-али» (две руки). Затем он идет дальше, приговаривая «бе, бе» ..., пока не доходит до «самба-бе» и «самба-али» (одна нога, две ноги). Если нужно считать дальше, папуас пользуется пальцами рук и ног кого-нибудь другого».
Вслед за возникновением и развитием чисел появилась и замечательная наука об их свойствах и законах, ими управляющих: «теория чисел».
Если покопаться в огромном массиве чисел, которых больше, чем руды в земле, то можно найти свойства интересные и удивительные, диковинные и забавные, неожиданные и курьезные

у людей лишь после того, как у них образовались

некоторые представления о целых числах.
Как и понятие целого числа, понятие дроби создалось не сразу.
Представление о «половине» возникло гораздо раньше, чем о «третях» и «четвертях», а об этих последних — раньше, чем о дробях с другими знаменателями.
Первые представления о целом числе возникли в процессе счета; первые представления о дробях — из процесса измерения (длин, площадей, веса и т. д.).
Наши «обыкновенные» дроби широко употреблялись древними греками и индийцами. Правила действий с дробями, изложенные индийским ученым Брамагуптой (VIII в.), лишь немногим отличаются от наших.
Наша запись дробей тоже совпадает с индийской; только дробной черты индийцы не писали; греки записывали сверху знаменатель, а снизу числитель, но чаще пользовались другими записями, например писали (конечно, своими знаками) 3 5х (три пятых).
Индийское обозначение дробей и правила действий над ними были усвоены в IX в. в мусульманских странах благодаря Мухаммеду Хорезмскому (аль-Хваризми). Они были перенесены в Западную Европу итальянским купцом и ученым Леонардо Фибоначчи из Пизы (XIII в.).
Наряду с «обыкновенными» дробями применялись (преимущественно в астрономии) шестидесятеричные дроби. Они были позднее вытеснены десятичными дробями. Последние впервые ввел выдающийся самаркандский ученый Гиясэддин Джемшид ал-Каши (XIV—XV вв.). В Европе десятичные дроби были введены в практику голландским купцом и выдающимся инженером-ученым Симоном Стевином (1548— 1620 гг.).

начать? Начните с формулировки задачи.
Что я могу сделать? Представьте

себе задачу как целое, как можно яснее и нагляднее. Пока не вдавайтесь в детали.
Мы вникаем в задачу.
С чего мне начать? Начните опять с формулировки задачи. Начните тогда, когда задача стала столь ясной и столь прочно запечатлелась в вашем сознании, что вы в состоянии на время расстаться с ней без риска забыть ее.
Что я могу сделать? Разделите задачу на главные элементы. Изучите главные элементы вашей задачи, рассматривая их поодиночке, затем последовательно одну за другой, затем в разнообразных сочетаниях, сопоставляя каждую деталь с другими деталями и со всей задачей в целом.
Чего я смогу этим добиться? Вы сможете разобраться в деталях задачи, которые впоследствии, вероятно, будут играть определенную роль.
Мы ищем плодотворную идею
С чего мне начать? Начинайте с рассмотрения главных элементов задачи.
Что я могу сделать? Рассмотрите задачу с различных сторон и найдите ее точки соприкосновения с вашими ранее приобретенными знаниями. Старайтесь вспомнить, что вам помогало прежде в подобных случаях.
В чем может состоять плодотворность идеи? Такая идея указывает вам весь путь или его часть; она более или менее ясно подсказывает вам, как нужно действовать. Идеи бывают более или менее полные. Вам повезло, если у вас есть хоть какая-нибудь идея.
Что мне делать с неполной идеей? Надо ее рассмотреть. Если она оставляет впечатление полезной в той или иной мере, вам следует рассмотреть ее подробнее. Если кажется, что на нее можно опереться, нужно проверить, как далеко вы можете продвинуться при ее помощи, и вновь рассмотреть создавшееся положение. Ситуация изменилась благодаря тому, что теперь у вас имеется полезная идея.
Чего я смогу этим добиться? Вам может повезти, вы можете натолкнуться на новую идею. Возможно, следующая идея приведет вас прямо к решению. Даже если пока вам не удается натолкнуться на какую-нибудь ценную новую идею, вы должны быть довольны уже тем, что приходите к более полному, более связному, более однородному восприятию задачи.

счастливой идеи, приведшей вас к решению. Начинайте, когда вы

уверены в том, что крепко ухватили главную мысль, и чувствуете себя в состоянии проанализировать детали, которые могут понадобиться.
Что я могу сделать? Закрепите свой успех. Выполните во всех деталях те алгебраические или геометрические действия, которые вы предварительно сочли выполнимыми. Убедитесь в правильности каждого шага. Если задача очень сложна, вы можете различать «большие» шаги и «малые» шаги, разделяя каждый большой шаг на несколько малых. Проверяйте вначале большие шаги, а затем переходите к малым.
Чего я смогу этим добиться? Того
Мы оглядываемся назад
С чего мне начать? С решения, полного и правильного в каждой своей детали.
Что я могу сделать? Рассмотрите решение с различных сторон и найдите точки соприкосновения с вашими ранее приобретенными знаниями.
Рассмотрите детали решения, стараясь максимально упростить их; обратите внимание на громоздкие части решения и попытайтесь сделать их короче; постарайтесь, охватить все решение одним взглядом.
Постарайтесь улучшить малые или большие части решения и усовершенствовать все решение в целом, сделать его интуитивно ясным.
Вглядитесь в метод, приведший вас к решению; постарайтесь выяснить, что в нем является главным, и применить его к другим задачам.
Всмотритесь в результат и попытайтесь использовать его, чтобы решить другие задачи.
Чего я смогу этим добиться? Вы можете найти новое, лучшее решение, можете обнаружить новые интересные факты. Во всяком случае, если вы приобретете привычку рассматривать и оценивать полученные решения указанным образом, вы сможете пополнить свои знания новыми, приведенными в стройную систему и готовыми к применению, и развить свои способности к решению задач.

Как решить задачу

очень вкусно поджаривает ломтики хлеба, пользуясь специальной маленькой сковородкой.

Поджарив одну сторону каждого ломтика, она переворачивает его на другую сторону. Поджаривание каждой стороны ломтика длится 30 секунд, причем на сковородке умещается рядом только два ломтика.
Сообразите, каким образом при этих условиях мама поджаривает обе стороны трех ломтиков только за 1½ минуты, а не за 2, и вы получите к ужину 3 вкусных поджаренных ломтика.
Ответ. Искусная кулинарка кладет два ломтика на сковородку и поджаривает одну их сторону в течение 30 сек. Затем первый ломтик она повертывает на другую сторону, а второй ломтик вынимает и кладет на его место третий. Таким образом, во вторую полминуту первый ломтик будет готов полностью, а третий — наполовину. Теперь она имеет 2 ломтика (второй и третий), каждый из которых готов наполовину. Их поджаривание будет закончено в следующие полминуты.
Общее время, как видите, 1½ минуты, а не 2.
 

« Перепись школы»

«Доля мальчиков и девочек »

« Книжный двор»

«Цветочные доли»

долю по числу учащихся занимает наш класс по сравнению

с общим количеством школьников? 
Задание: узнать общее число учащихся в нашей школе, количество девочек и мальчиков по школе ; составить дроби, показывающие долю 5 класса в нашей школе, долю девочек и мальчиков от числа всех учащихся.

Выполнение задания.
Мы обратились за помощью к завучу по УР Пыховой Г.В. и социальному педагогу нашей школы Федечкиной Т.В.
Они предоставили нам количество всех учащихся нашей школы, количество девочек и мальчиков по школе, на начало года и на начало второго полугодия. 
Мы провели необходимые подсчёты и по их результатам составили таблицы и диаграммы.