- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Методика дифференцированного подхода в обучении на уроках математики
Содержание
- 2. Дифференциация как система
- 3. Виды дифференциации:
- 4. Индивидуальные особенности учащихся и их учет в
- 5. Организация дифференциального подхода в обучении математике.
- 6. ДИФФЕРЕНЦИАЦИЯ МЕТОДОВ И ФОРМ, ИСПОЛЬЗУЕМЫХ ПРИ ОБУЧЕНИИ математике
- 7. КЛАССИФИКАЦИЯ РАЗЛИЧНЫХ СПОСОБОВ ОРГАНИЗАЦИИ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ В УСЛОВИЯХ ДИФФЕРЕНЦИРОВАННОГО ОБУЧЕНИЯ
- 8. ОРГАНИЗАЦИЯ ДИФФЕРЕНЦИРОВАННОГО ПОДХОДА НА РАЗЛИЧНЫХ ЭТАПАХ УРОКА:
- 9. Второй этап. а) самостоятельные работы учащихся
- 10. Третий этап. Работа с учебникомПри работе с
- 11. Четвертый этап. Дифференцированный контроль подготовленности к урокуН.В.Метельский
- 12. Пятый этап. Домашние заданияМ.М. Рассудовская предлагает составлять
- 13. Методика дифференцированной работы на уроке
- 14. Заключение.Итак, какая же реальная польза от применения
- 15. Скачать презентацию
- 16. Похожие презентации
Дифференциация как система













Слайд 4 Индивидуальные особенности учащихся и их учет в процессе
обучения математике. Типологические группы учащихся
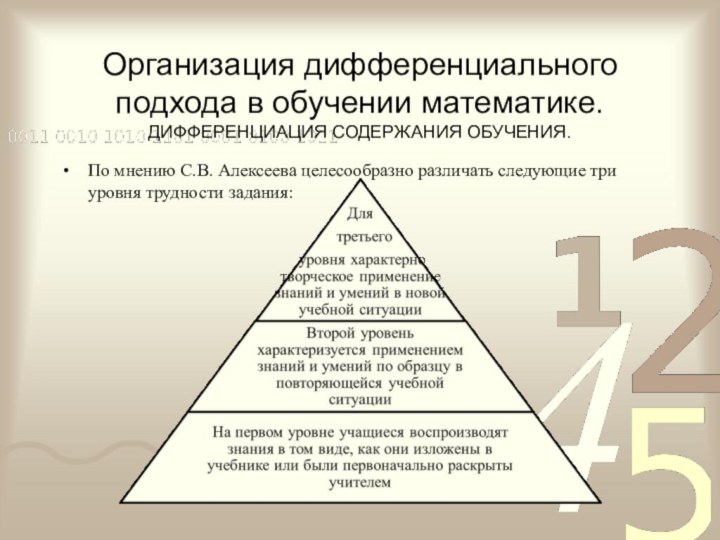
группы:Слайд 5 Организация дифференциального подхода в обучении математике. ДИФФЕРЕНЦИАЦИЯ СОДЕРЖАНИЯ
ОБУЧЕНИЯ.
По мнению С.В. Алексеева целесообразно различать следующие три уровня
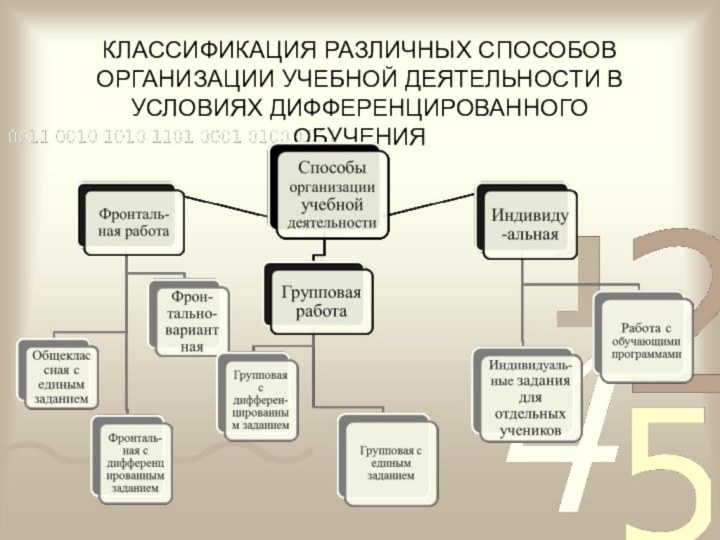
трудности задания: Слайд 7 КЛАССИФИКАЦИЯ РАЗЛИЧНЫХ СПОСОБОВ ОРГАНИЗАЦИИ УЧЕБНОЙ ДЕЯТЕЛЬНОСТИ В УСЛОВИЯХ
ДИФФЕРЕНЦИРОВАННОГО ОБУЧЕНИЯ
Слайд 8 ОРГАНИЗАЦИЯ ДИФФЕРЕНЦИРОВАННОГО ПОДХОДА НА РАЗЛИЧНЫХ ЭТАПАХ УРОКА: Первый этап.
Введение нового материала.
На первом уровне ученики самостоятельно ведут поиск.
Учитель указывает лишь результат, формулирует саму проблему.На втором уровне, т.е. для другой группы учащихся, учитель указывает на проблему, но не сообщает конечного результата, ученики сами формулируют проблему.
На третьем уровне учитель не указывает на проблему, а постепенно подводит учащихся к тому, что они самостоятельно усматривают ее.
Слайд 9 Второй этап. а) самостоятельные работы учащихся по изучению
нового, б) самостоятельные работы по применению изученной теории к решению
задач
Слайд 10
Третий этап. Работа с учебником
При работе с учебником
задания, предлагаемые учащимся, также могут быть дифференцированы. Например, одной
группе учащихся предлагается прочитать теорему и выделить все шаги доказательства, другой – план доказательства; третьей группе предлагаются задания с пропусками и т.д.
Слайд 11
Четвертый этап. Дифференцированный контроль подготовленности к уроку
Н.В.Метельский предлагает
на каждом уроке математики проводить фронтальный письменный опрос всех
учащихся класса одновременно в двух вариантах на 10 минут. Он подчеркивает, что такие письменные опросы целесообразно проводить отдельно по трем основным компонентам содержания:а) формулировка определений, теорем, правил и т. п. (типа математического диктанта);
б) доказательствам;
в) решению задач (выполнение упражнений)
Слайд 12
Пятый этап. Домашние задания
М.М. Рассудовская предлагает составлять дифференцированные
домашние задания, которые могли бы более полно использовать возможности
учащихся и позволили бы организовать их проверку в классе. Принцип составления таких упражнений заключается в том, что первое упражнение предназначено для всего класса, а второе непосредственно связано с первым, но содержит по сравнению с первым некоторую дополнительную трудность
Слайд 14
Заключение.
Итак, какая же реальная польза от применения дифференцированного
обучения?
- Значительно улучшается четкость в организации работы класса. Четкость
в работе дает возможность постоянно контролировать знания, умения, навыки. - Заметно увеличиваются возможности для работы с сильными учениками, поскольку учитель уже не должен спрашивать данный на уроке материал в полном объеме со всех учащихся.
- Кроме того, отпадает необходимость разгружать программу и снижать общий уровень требований, оглядываясь на слабых учащихся.