Слайд 2
Дворец знаний
на
Рациональные числа
+
-
Арифметические действия
Натуральные числа
Обыкновенные дроби
Десятичные дроби
Делимость чисел
НОД
и НОК
Основное свойство дроби
Смешанные числа
Дробные выражения
5
К
Л
А
С
С
Положительные числа
Отрицательные числа
+
-
Умножение и
деление обыкновенных дробей
Сложение и вычитание дробей с разными знаменателями
Раскрытие скобок
Подобные слагаемые
Геометрический
материал
Решение задач
Решение уравнений
Координаты на плоскости
Слайд 3
Повторение
Выполните действия:
23,47-19,584+10,2 ;
401-(0,83+81,2-12,163) ;
57,08*3,9 ;
0,043*20,8 ;
33,947:8,3 ;
0,13:0,052
.
Решите уравнение:
(301 –х)*54=10962 ;
3,9+5,2х-1,6х=18,48.
Слайд 4
Ответы
Выполните действия:
14,086 ;
331,133 ;
222,612 ;
0,8944 ;
4,09 ;
2,5 .
Решите
уравнение:
98 ;
4,05 .
Слайд 5
Делимость чисел
1.Делители и кратные.
Делителем натурального числа а называют
натуральное число,на которое а делится без остатка.
Делители 12:
1; 2; 3; 4; 6 и 12
Кратным натурального числа а называют натуральное число, которое делится без остатка на а.
Кратные 8: 8; 16; 24; 32; 40...
Слайд 6
Признаки делимости
Если запись натурального числа оканчивается цифрой 0,то
это число делится на 10 без остатка.
280 : 10=28
Если
запись натурального числа оканчивается цифрой 0 или 5, то это число делится на 5.
280 : 5=58 и 285 : 5=59
Если запись натурального числа оканчивается цифрой 0; 2; 4; 6; 8 (ЧЕТНОЙ ЦИФРОЙ), то число делится на 2.
282; 284; 280; 286; 288
Слайд 7
Признаки делимости
Если сумма цифр делится на 9,то и
число делится на 9.
549: 5+4+9 = 18, 18 :
9 = 2, ЗНАЧИТ И 549 ДЕЛИТСЯ НА 9.
Если сумма цифр делится на 3,то и число делится на 3.
666: 6+6+6 = 18, 18 : 3 = 6, ЗНАЧИТ И 666 ДЕЛИТСЯ НА 3.
Слайд 8
Разложение на простые множители.
Разложим число 756 на простые
множители:
756 2
378 2
189 3
63 3
21 3
7 7
1
756=223337
Слайд 9
Простые и составные числа
Натуральное число называют простым, если
оно имеет только два делителя: единицу или само число.
Натуральное число называют составным, если оно имеет более двух делителей.
Число 1 имеет только один делитель: само это число. Поэтому его не относят ни к составным, ни к простым. Любое составное число можно разделить на два множителя, каждый из которых больше 1.
Такие числа как 9 и 18 называют составными,так как
у 9 и 18 несколько делителей.
Делители 9: 1; 3; 9.
Делители 18: 1; 2; 3; 6; 18.
Такие числа как 5 и 7 называют простыми, так как у 5 и 7 по два делителя.
Делители 5: 1; 5.
Делители 7: 1; 7.
Слайд 10
НОД
Наибольший общий делитель.
Наибольшее натуральное число,на которое делятся без
остатка числа a и b, называют наибольшим общим делителем
этих чисел.
Делители 24: 1; 2; 3; 4; 6; 8; 12; 24.
Делители 35: 1; 5; 7; 35.
Натуральные числа называют взаимно простыми, если их наибольший общий делитель равен 1.
Алгоритм нахождения НОД(а;в):
1.Разложить числа а и в на простые множители;
2.Из множителей , входящих в разложение одного из этих чисел вычеркнуть те,которые не входят в разложение других чисел;
3.Найти произведение оставшихся множителей.
Слайд 11
Пример.
1. Найти НОД (18;42)
18=2*3*3;
42=2*3*7;
НОД(18;42)=2*3=6.
2. Найти НОД(60;105)
60=2*2*3*5;
105=3*5*7;
НОД(60;105)=3*5=15.
Слайд 12
Найти НОД:
I вариант
18 и 24;
13 и 26;
35 и
56;
54 и 81
112 и 144;
12, 28 и 80.
II вариант
12
и 28;
17 и 34;
27 и 45;
48 и 64;
156 и 192;
18, 27и 90.
Слайд 13
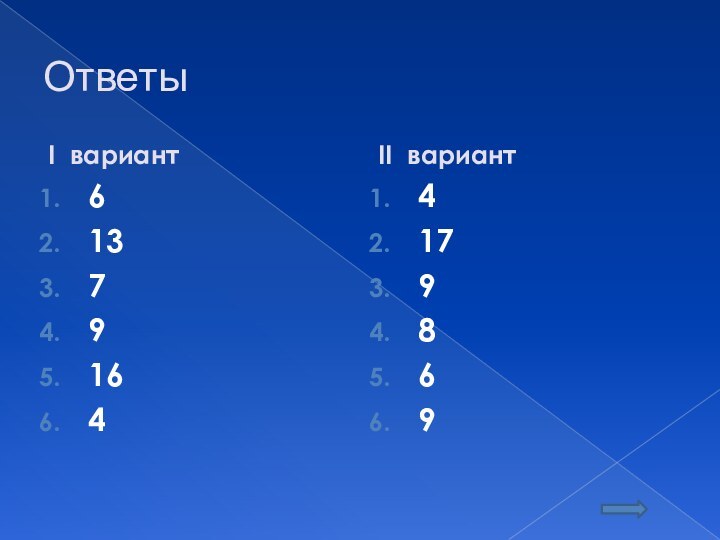
Ответы
I вариант
6
13
7
9
16
4
II вариант
4
17
9
8
6
9
Слайд 14
НОК
Наименьшее общее кратное.
Наименьшим общим
кратным натуральных чисел a и b называют натуральное число,
которое кратно a и b.
Алгоритм нахождения НОК(а;в):
1. Разложить а и в на простые множители;
2. выписать множители, входящие в разложение одного из чисел;
3. добавить к ним недостающие множители из разложений остальных чисел;
4. найти произведение получившихся множителей.
Слайд 15
Пример
1. Найти НОК(18;42)
18=2*3*3;
42=2*3*7;
НОД(18;42)=2*3*3*7=126
2. Найти НОК(60;105)
60=2*2*3*5;
105=3*5*7;
НОД(60;105)=2*2*3*5*7=420
Слайд 16
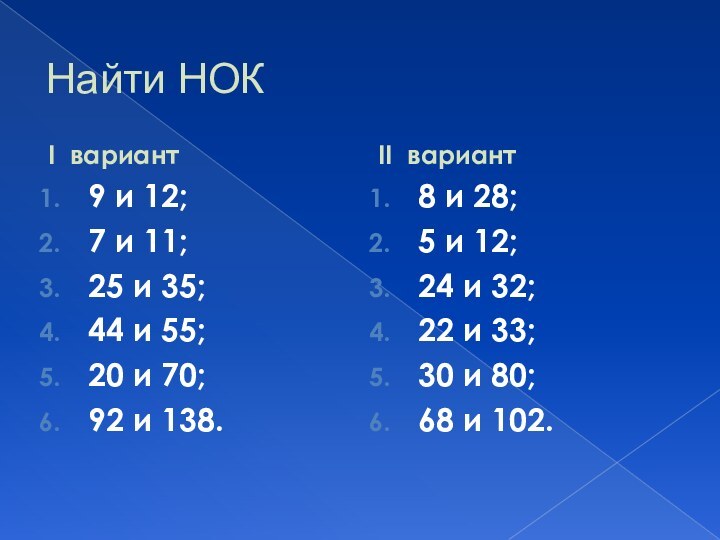
Найти НОК
I вариант
9 и 12;
7 и 11;
25 и
35;
44 и 55;
20 и 70;
92 и 138.
II вариант
8 и
28;
5 и 12;
24 и 32;
22 и 33;
30 и 80;
68 и 102.
Слайд 17
Ответы
I вариант
36
77
175
220
140
276
II вариант
56
60
96
66
240
204
Слайд 18
Основное свойство дроби
Если числитель и знаменатель дроби умножить
или разделить на одно и то же натуральное число,
то получится равная ей дробь.
Сокращение дробей.
Деление числителя и знаменателя на их общий делитель называют сокращением дробей.
Слайд 21
Сложение и вычитание дробей с разными знаменателями
Чтобы сравнить,сложить
или вычесть дроби с разными знаменателями,надо:
1.Привести данные дроби к
наименьшему общему знаменателю;
2.Сравнить (сложить, вычесть) полученные дроби.
Чтобы привести дроби к наименьшему общему знаменателю,надо:
1.Найти наименьшее общее кратное знаменателей этих дробей;
2.Разделить наименьший общий знаменатель на знаменатель данных
дробей;
3.Умножить числитель и знаменатель каждой дроби на её дополнительный
множитель.
Слайд 23
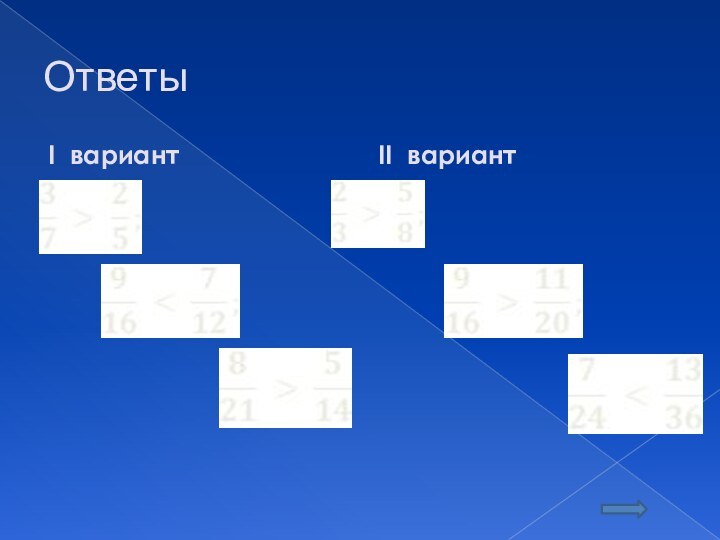
Сравнить дроби
I вариант
I I вариант
Слайд 25
Смешанные числа
Чтобы сложить смешанные числа,надо:
1.Привести дробные части этих
чисел к наименьшему
общему знаменателю;
2.Отдельно выполнить сложение целых частей и
отдельно дробных частей. Если при сложении дробных частей поучилась неправильная дробь,выделить целую часть из этой дроби и прибавить её к полученной целой части.
Слайд 26
Смешанные числа
Чтобы выполнить вычитание смешанных чисел,надо:
1.Привести дробные части
этих чисел к наименьшему общему знаменателю;
2.Отдельно выполнить вычитание целых
частей и отдельно дробных частей. Если дробная часть уменьшаемого меньше дробной части вычитаемого,превратить её в неправильную дробь, уменьшив на единицу целую часть.
Слайд 28
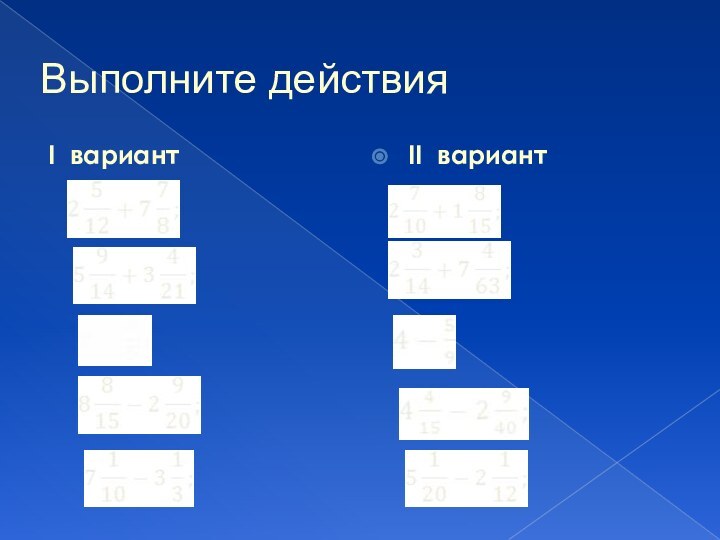
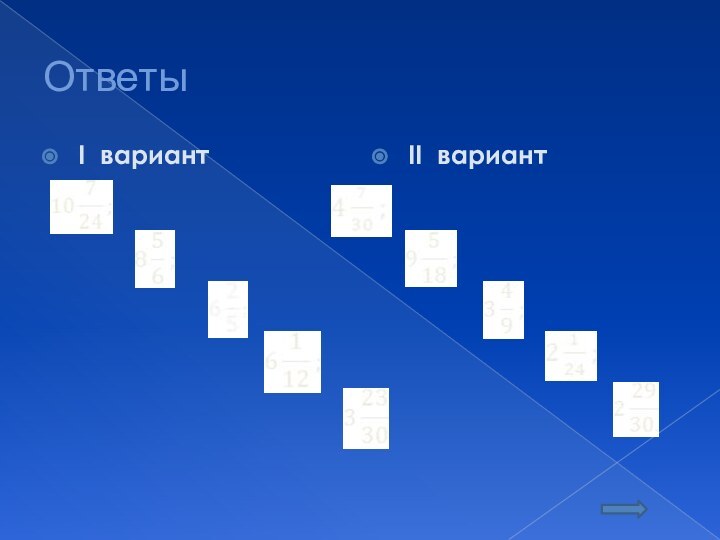
Выполните действия
I вариант
II вариант
Слайд 30
Умножение и деление обыкновенных дробей
Чтобы умножить дробь на
натуральное число,надо её числитель умножить на это число,а знаменатель
оставить без изменения.
Чтобы умножить дробь на дробь,надо:
1)найти произведение числителей и знаменателей этих дробей;
2)первое произведение записать числителем,а второе-знаменателем.
Для того чтобы выполнить умножение смешанных чисел,надо их записать в виде неправильных дробей,а затем воспользоваться правилом умножения дробей.
Слайд 31
Умножение и деление обыкновенных дробей
Чтобы разделить одну дробь
на другую,надо делимое умножить на число,обратное делителю.
;
Слайд 32
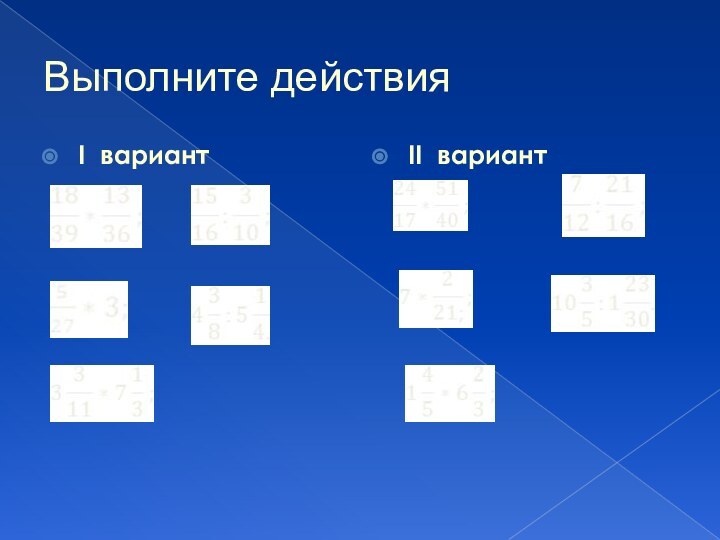
Выполните действия
I вариант
II вариант
Слайд 34
Дробные выражения
Частное двух чисел или выражений, в котором
знак деления обозначен чертой, называют дробным выражением.
Слайд 35
Задачи на дроби
Нахождение дроби от числа
Чтобы найти дробь
от числа,нужно умножить число на эту дробь.
Между двумя населенными
пунктами 160 км. Автомобилист проехал пути. Сколько километров проехал автомобилист?
(км) проехал автомобилист.
Слайд 36
Задачи на дроби
Задачи на нахождение числа по его
дроби.
Чтобы найти число по данному значению его дроби,надо это
значение разделить на дробь.
Девочка прочитала 150 страниц,что составило всей книги. Сколько страниц в книге?
(стр.) в книге.
Слайд 37
Задачи на дроби
Задачи на нахождение отношения величин.
Чтобы найти,
какую часть одно число составляет от другого, надо первое
число разделить на второе.
В классе 32 человека. Из них 18 составляют девочки. Какую часть всех учащихся составляют девочки?
Слайд 38
Реши задачи
Длина экватора Земли равна примерно 40000 км,
а ее диаметр составляет длины экватора.
Чему равен диаметр Земли?
Ширина Керченского пролива 4,3, что составляет 1/20 ширины Беренгова пролива. Какова ширина Беренгова пролива?
Кусок латуни массой 5 кг содержит 3 кг меди. Какую часть этого куска составляет медь? Вырази полученную часть в процентах.
Слайд 39
Положительные и отрицательные числа.
Координаты на прямой.
Числа со знаком
«+» называют положительными.
Числа со знаком «−» называют отрицательными.
Прямую с
выбранными на ней началом отсчёта, единичным отрезком и направлением называют координатной прямой.
Число, показывающее положение точки на прямой, называют координатой этой точки.
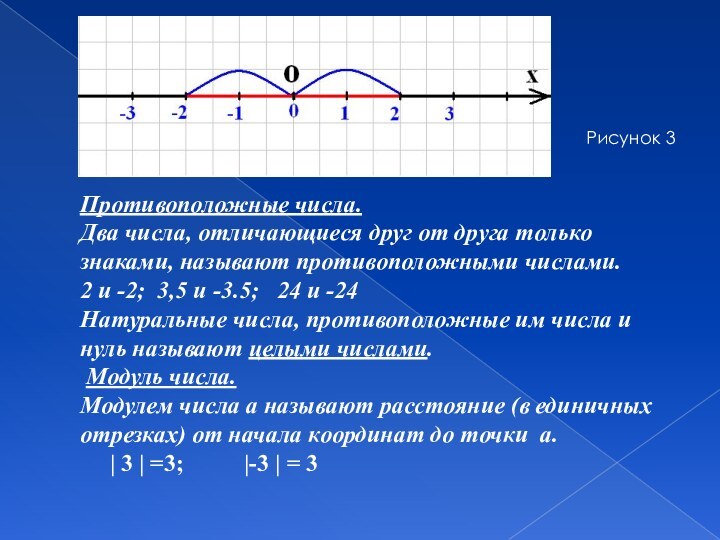
Рисунок 2
Слайд 40
Противоположные числа.
Два числа, отличающиеся друг от друга только
знаками, называют противоположными числами.
2 и -2; 3,5 и -3.5;
24 и -24
Натуральные числа, противоположные им числа и нуль называют целыми числами.
Модуль числа.
Модулем числа а называют расстояние (в единичных отрезках) от начала координат до точки а.
3 =3; -3 = 3
Рисунок 3
Слайд 41
Сравнение чисел.
Любое отрицательное число меньше любого положительного числа.
-6714.
Из двух отрицательных чисел меньше то, модуль которого больше.
-52 -25.
Нуль больше любого отрицательного числа, но меньше любого положительного числа.
0 12,4; 0 -146,7.
Слайд 42
Сравните
I вариант
-258 и 259;
-0,05 и -0,005;
3,25 - и
-3,3;
;
-
;
.
II вариант
362 и -363;
-0,002 и -0,02;
-6,45 и 6,8;
;
;
.
Слайд 43
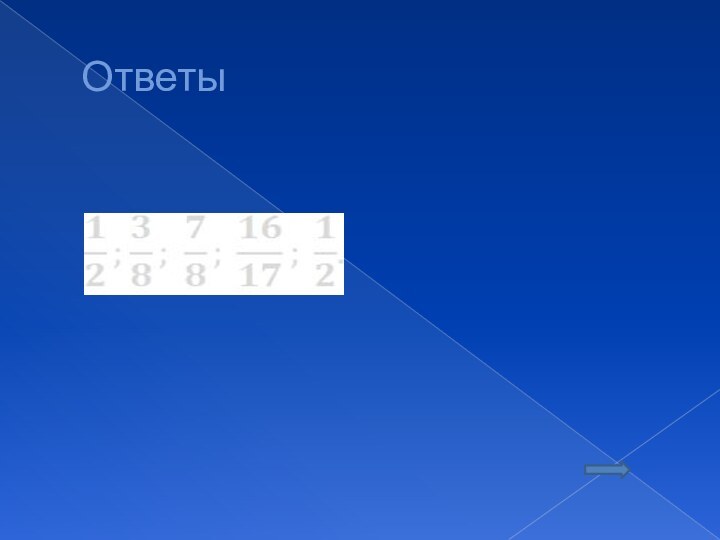
Ответы
II вариант
;
;
;
;
;
.
II вариант
;
;
;
;
;
.
Слайд 44
Сложение и вычитание отрицательных чисел
Сложение чисел с помощью
координатной прямой.
Прибавить к числу а число b – значит
изменить число а на b единиц. Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.
Сумма двух противоположных чисел равна нулю.
-51+51=0;
32+(-32)=0.
Слайд 45
Сложение отрицательных чисел
Сложение отрицательных чисел.
Чтобы сложить два отрицательных
числа, надо: 1) сложить их модули; 2)поставить перед полученным
числом знак «−».
-12+(-15)=-(12+15)=-27.
Сложение чисел с разными знаками.
Чтобы сложить два числа с разными знаками, надо: 1) из большего модуля слагаемых вычесть меньший; 2) поставить перед полученным числом знак того слагаемого, модуль которого больше.
-8+13=13-8=5;
24+(-29)=-(29-24)=-5.
Слайд 46
Выполни сложение
I вариант
-18+15;
-1,9+2;
6,4+(-8);
-5,2+0;
;
.
II вариант
14+(-16);
1,2+(-0,9);
-1,3+6;
0+(-0,15);
;
.
Слайд 47
Ответы
I вариант
-3
0,1
-1,6
-5,6
0
0,95
II вариант
-2
0,3
4,7
-0,15
-2
-3,4
Слайд 48
Вычитание отрицательных чисел
Чтобы из данного числа вычесть другое,
надо к уменьшаемому прибавить число, противоположное вычитаемому:
a-b =a+(-b).
-12-15=-12+(-15)=-27;
7-24=7+(-24)=-17;
9-(-2)=9+2=11;
-5-(-11)=-5+11=6.
Слайд 49
Выполни вычитание
I вариант
-1,8-3,4;
-7,8-3,4;
0-(-4,5);
;
;
;
II вариант
-1,6-(-2,5);
-6,3-0;
-5,1-(-5,1);
;
;
;
Слайд 50
Ответы
I вариант
-5,2 ;
-11,2 ;
4,5 ;
;
;
;
-9
II вариант
0,9 ;
-6,3 ;
0 ;
;
;
;
.
Слайд 51
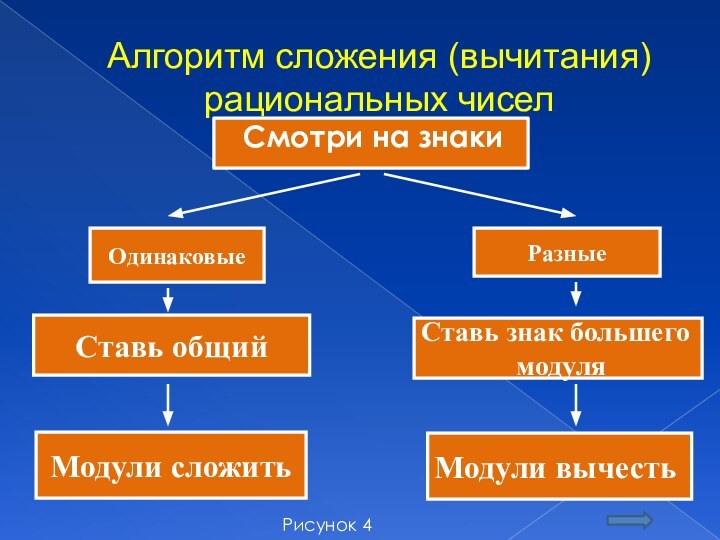
Алгоритм сложения (вычитания) рациональных чисел
Смотри на знаки
Одинаковые
Разные
Ставь общий
Модули
сложить
Ставь знак большего
модуля
Модули вычесть
Рисунок 4
Слайд 52
Умножение положительных и отрицательных чисел
Чтобы перемножить два числа
с разными знаками, надо перемножить модули этих чисел и
поставить перед полученным числом знак «-».
(-2,4) · 6 = -(2,4 · 6) = -14,4;
2,4 · (-6) = -(2,4 · 6) = -14,4.
При изменении знака любого множителя знак произведения меняется, а его модуль остается тем же.
Чтобы перемножить два отрицательных числа, надо перемножить их модули.
(-7) · (-9) = |-7| · |-9| = 7 · 9 = 63;
(-10) · (-15) = |-10| · | -15| = 150.
Слайд 53
Вычислить:
I вариант
13*(-11);
-2,5*(-0,1);
-0,36*0,5;
-1,2*(-0,12);
0,01*(-1000);
;
;
.
II вариант
-15*26;
-1,3*(-0,01);
0,2*(-6,5);
-0,11*(-1,1);
10*(-0,001);
;
;
.
Слайд 54
Ответы
I вариант
-143 ;
0,25 ;
-0,18 ;
0,144 ;
-10 ;
;
;
4.
II вариант
-390 ;
0,013
;
-1,3 ;
0,121 ;
-0,01 ;
;
;
14.
Слайд 55
Деление положительных и отрицательных чисел
Чтобы разделить отрицательное число
на отрицательное, надо разделить модуль делимого на модуль делителя.
-9
: (-3) = 3; -30 : (-5) = 6.
При делении чисел с разными знаками, надо:
разделить модуль делимого на модуль делителя;
поставить перед полученным числом знак «-».
Обычно вначале определяют и записывают знак частного, а потом уже находят модуль частного.
66 : (-11) = -6; -56 : 4 = -14.
При делении нуля на любое число, не равное нулю, получается нуль.
Делить на нуль нельзя!
Слайд 56
Вычислить
I вариант
276:(-138);
-0,98:1,4;
-266,2:(-4,4);
-153:(-7,5);
;
;
II вариант
576:(-8);
-7,5:(-0,5);
-14,21:4,9;
5,552:(-1,6);
;
.
Слайд 57
Ответы
I вариант
-2 ;
-0,7 ;
60,5 ;
20,4 ;
;
.
II вариант
-72 ;
15 ;
-2,9
;
-3,47 ;
;
.
Слайд 58
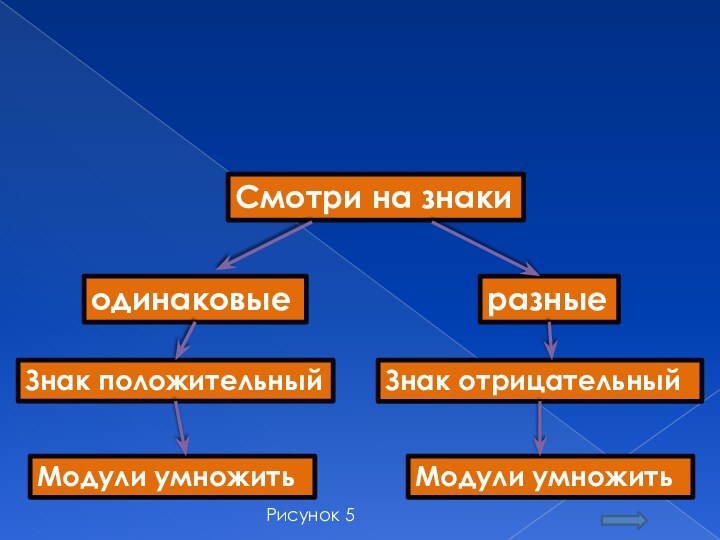
Смотри на знаки
одинаковые
разные
Знак положительный
Знак отрицательный
Модули умножить
Модули умножить
Рисунок 5
Слайд 59
Свойства действий с рациональными числами
1. Переместительное свойствами:
a +
b = b + a, ab = ba
2.
Сочетательное свойство:
a + (b + c) = (a + b) + c, a(bc) = (ab)c.
3. Распределительное свойство :
(a + b) · c = ac + bc.
4. a + 0 = a, a + (-a) = 0.
5. a ·1 = a, a · = 1, если a 0.
6. a · 0 = 0.
7. Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если a · b = 0, то либо a = 0, либо b = 0 (или а = 0 и b = 0).
Слайд 60
Раскрытие скобок
Раскрытие скобок
a + (b + c)
= a + b + c.
Если перед скобками
стоит знак «+», то можно опустить скобки и этот знак «+», сохранив знаки слагаемых, стоящих в скобках. Если первое слагаемое в скобках записано без знака, то его надо записать со знаком «+».
-10 + (12 - 7) = -10 + 12 - 7 = -5.
Чтобы записать сумму, противоположную сумме нескольких слагаемых, надо изменить знаки данных слагаемых.
- (a + b) = -a - b.
40 - (30 - 25 + 5) = 40 - 30 + 25 - 5 = 30.
Чтобы раскрыть скобки, перед которыми стоит знак
«-», надо заменить этот знак на «+», поменяв знаки всех слагаемых в скобках на противоположные, а потом раскрыть скобки.
25 - (34 - 14 - 10 + 5) = 25 - 34 + 14 + 10 - 5 = 10.
Слайд 61
Раскрытие скобок
Раскрытие скобок
Распределительное свойство умножения:
(a + b)
· c = ac + bc
Замену выражения (a
+ b)·c выражением ac + bc или выражения c·(a + b) выражением ca + cb также называют раскрытием скобок.
6 · (2a + 3b) = 12a + 18b;
-2 · (a - b) = -2a + 2b.
Слайд 62
Раскрыть скобки
I вариант
17,24+(7,9-9,14) ;
24,16-(3,9-14,74) ;
;
.
II вариант
6,83+(8,4-2,13) ;
11,12-(4,8-3,68) ;
;
.
Слайд 63
Ответы
II вариант
1,6 ;
35 ;
;
.
II вариант
13,1 ;
10 ;
;
.
Слайд 64
Коэффициент.
Коэффициент
Если выражение является произведением числа и одной
или нескольких букв, то это число называют числовым коэффициентом
(или просто коэффициентом).
23а · 3b = 69ab; 4a · (-10) = -40a.
Коэффициентом такого выражения, как a или ab, считают 1, так как а = 1 · а; ab = 1 · ab.
При умножении -1 на любое число а получается число –а:
-1 · а = -а.
Поэтому числовым коэффициентом выражения –а считают число -1.
Слайд 65
Подобные слагаемые
Слагаемые, имеющие одинаковую буквенную часть, называют подобными
слагаемыми.
Чтобы сложить (или говорят: привести) подобные слагаемые, надо сложить
их коэффициенты и результат умножить на общую буквенную часть.
-12а - 10а + 7а + 6а = -9а;
24b - 23b + 40b + 5b = 46b.
Слайд 66
Привести подобные слагаемые
I вариант
1. 12a-17b+13b-15a+2a ;
2.
;
3. 0.2*(2.1x-2.3y)- -0.4*(3.1y+1.9x).
II вариант
1. -5k+12p-8k-13p+7k ;
2. ;
3. (-0.7x+0.6y)*5 – - 3*(0.4y- 1.5x).
Слайд 67
Ответы
I вариант
-a-4b ;
;
-0.34x-1.7y.
II вариант
-6k-p ;
;
x+1.8y
Слайд 68
Решение уравнений
Равенство с переменной называют уравнением.
23,5-2х=х+11,5
Значения переменной, при
каждом из которых уравнение обращается в верное числовое равенство
называются корнями уравнения.
При х=4 23,5-2*4=4+11,5 ;
15=15.
Число 4 - корень уравнения.
Решить уравнение – это значит найти все его корни или доказать, что корней нет.
Слайд 69
Решение уравнений
Свойства уравнений
1. Корни уравнения не изменяются, если
обе части уравнения умножить или разделить на одно и
тоже число, не равное нулю.
4х + 7 = 27;
4х = 27 - 7;
4х = 20;
х = 20 : 4;
х = 5.
2. Корни уравнения не изменяются, если какое-нибудь слагаемое перенести из одной части уравнения в другую, изменив при этом его знак.
3х + 8 = 38;
3х = 38 – 8;
3х = 30;
х = 10.
Слайд 70
Решить уравнения:
I вариант
4у+21=5у+27;
7m-11=10m+16;
5.6+0.6x=0.3x-1.3;
0.4(6x-7)=0.5(3x+7);
7(1.4y+1.8)-7.6=10.1y;
.
II вариант
-2x+16=5x+30;
11m-7=-22+5m;
2.8-3.2a=-4.8-5.1a;
1.2(3b+5)=2(2.4b-3.6);
3.2(5x-1)=3.6x-9.4;
.
Слайд 71
Ответы
I вариант
-6 ;
-9 ;
-23 ;
7 ;
-50 ;
.
II вариант
-2 ;
-20,5 ;
-4 ;
11 ;
-0,5 ;
-9 .
Слайд 72
Решение задач
В одном ящике в 3 раза больше
слив, чем во втором. Если из первого ящика переложить
во второй 1 кг слив, то в первом станет в 2 раза больше слив, чем во втором. Сколько слив в каждом ящике?
В одном мешке в 2 раза меньше крупы, чем во втором. Если из второго мешка пересыпать в первый 5 кг крупы, а затем из первого отсыпать 2 кг, то крупы в обоих мешках станет поровну. Сколько крупы в каждом мешке?
Ширина прямоугольника составляет 20% его периметра, а длина равна 1,5 см. Найти площадь прямоугольника.
За три дня турист прошел 54 км. В первый день он прошел на 20% больше, чем во второй день, а в третий – половину пути, пройденного во второй день. Сколько километров прошел турист в первый день?
Слайд 73
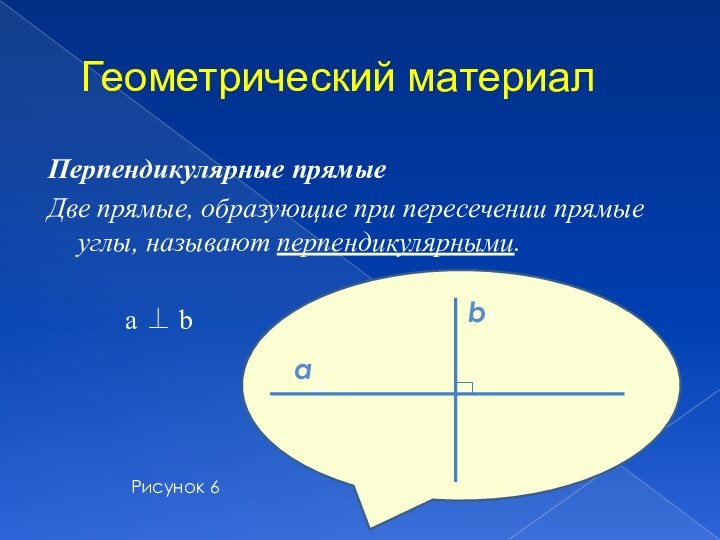
Геометрический материал
Перпендикулярные прямые
Две прямые, образующие при пересечении прямые
углы, называют перпендикулярными.
a
b
а
bв
a
Рисунок 6
Слайд 74
Геометрический материал
Параллельные прямые
Две непересекающиеся прямые на плоскости называют
параллельными.
a b
a
a
b
Рисунок 7
Слайд 75
Координаты на плоскости
Система координат на плоскости –
две
перпендикулярные прямые, которые пересекаются в начале отсчета – точке
О, с выбранным единичным отрезком и указанным положительным направлением.
х, у – координаты точки А;
х –абсцисса, у – ордината.
Рисунок 8
Слайд 76
Построй четырехугольник ABCD по координатам его вершин.
В
какой координатной четверти расположена точка С? Найти координаты точки
пересечения диагоналей четырехугольника ABCD.
A(-3;3) ;
B(-1;0) ;
C(3;-1) ;
D(1;2).
F(3;1) ;
B(-1;0) ;
C(-3;-3) ;
D(1;-2).