Слайд 2
С первых лет жизни и до глубокой старости
человек постоянно обращается к числам, фигурам, правилам, сложившимся в
математике. Просыпаясь, он обычно вспоминает, какой сегодня день, в котором часу ему нужно отправиться в школу или на работу и когда он возвратится домой. Днем ему неоднократно приходится подсчитывать, сколько, что стоит, сколько надо заплатить или получить, а прежде чем приготовить обед, придётся отмерить, сколько взять крупы, масла, муки и пр.
Словом, каждому из нас ежедневно приходится обращаться к математике, её правилам, которые мы изучили или ещё изучаем. Пользоваться основами математики стало для нас настолько обычным и естественным, что мы забываем: когда-то люди, наши предки , ничего этого не знали и, видимо, с большим трудом и продолжительное время открывали начала математики.
Рассказу о том, как люди учились считать, и посвящена наша работа.
Слайд 3
Цель работы
В прошлом году мы начали работу над
проектом под названием «Оформляем кабинет математики». В этом учебном
году решили продолжить работу над проектом и создать в отдельно взятом кабинете миниатюрный музей математики. Используя актуальную лексику — наномузей математики. Решили, пусть это будет обычный шкаф с полками на которых и разместятся экспонаты. Чтобы были они выполнены руками учащихся (кстати, с указанием авторов).
Слайд 4
Для работы над проектом 5 и 11 классы
поделили на группы.
Для успешного выполнения задания каждая группа должна
была найти ответ на свой вопрос. Мы расскажем вам о работе группы «Практики»
Слайд 5
Как люди научились считать?
Когда возникли современные математические
символы?
Как считали на Руси?
Когда появились первые счетные приборы?
Нам предстоит
ответить на вопросы:
Слайд 6
Практическая часть
Изготовить модель вычислительного прибора «Палочки Непера»
Создать
в нашем кабинете математики миниатюрный музей счетных приборов.
Слайд 7
Когда возникли современные символы математики?
Считать люди
научились еще в незапамятные времена. Первые математические понятия возникли
из их практических потребностей. Они были связаны с необходимостью пересчета людей, животных, предметов, денежными расчетами, с измерением земельных участков.
Название «арифметика» происходит от греческого слова «арифмос» - число.
Слайд 8
Клинописные таблицы
О развитии математики в Древнем мире рассказывают
папирусы, вавилонские клинописные таблицы и другие документы. Из Древних
Египетских папирусов наиболее известны два: один из них храниться в Москве, другой – в Лондоне. Они были написаны около 4000 тысяч лет назад.
Слайд 9
Вавилонская система
счисления
В настоящее время найдено
и расшифровано несколько сотен таких таблиц. В основе
системы счисления, принятой в Вавилоне, лежало число 60, а не 10, как у нас. Возникновение шестидесятеричной системы связано с денежными расчётами. В египетских папирусах, вавилонских клинописных таблицах обнаружены образцы решения арифметических задач: о разделе имущества, о вычислении площади поля.
Числа вавилоняне обозначали клинышками. Каждая единица стоящей слева группы клинышков, отделённых промежутком, обозначала 60.
Слайд 10
Хранение числовой информации
Для запоминания чисел древние люди пользовались
зарубками на деревьях, на палках или узлами на верёвках.
Слайд 11
Хранение числовой информации
Для хранения числовой информации на Руси
пользовались бирками. В истории, народном творчестве и литературных произведениях
много раз упоминается о счете при помощи зарубок и , в частности, при помощи бирок.
Слайд 12
Запись числа
Когда появилась нужда записывать большие числа, стало
неудобно пользоваться чёрточками и зарубками. Тогда стали вводить особые
знаки для отдельных чисел. Каждое число обозначалось особым значком – иероглифом.
В египетских иероглифах видны рисунки: число сто – свёрнутый пальмовый лист, тысяча – цветок лотоса, символ изобилия, сто тысяч – лягушка, так как во время разлива Нила было очень много лягушек.
Слайд 13
Ионийский способ записи числа
Примерно в V веке нашей
Эры появился ионийский способ записи числа. Первые девять букв
греческого алфавита обозначали числа от1 до 9. Следующие 9 букв – десятки, затем –сотни . Те же буквы со специальными знаками обозначали числа больше 1000. Ионийская система записи чисел была шагом вперед по сравнению с египетскими и вавилонскими способами. Возникла она из потребностей торговли. Этой нумерацией пользовался знаменитый древнегреческий ученый Архимед. В своей книги «о числе песка» он расширил границы применения ионийской нумерации и установил способ умножения степеней числа 10.
Слайд 14
Современные цифры
Мы узнали, что современные цифры, как и
современная нумерация, возникли в Индии. В течение многих столетий
они много раз изменялись. Десятичную позиционную систему записи чисел, которой мы пользуемся сейчас, изобрели индусы 2000 лет назад, в последствии пропущенные разряды стали обозначать кружком(нулём), чем и было завершено создание современного способа записи чисел.
Однако современные начертания чисел пришли к нам не из Индии, а из мавританских арабских стран. Заимствовав у индусов десятичный способ записи чисел, арабы стали применять свои знаки. Из них возникли современные цифры.
Слайд 15
Римские цифры
Несмотря на большие преимущества индийской нумерации,
она была принята в Западной Европе лишь в семнадцатом
веке. До этого применялись только римские цифры. Со временем такие записи чисел оказались очень неудобными. Всем известны римские цифры:
Римляне обозначали тысячу буквой m. Вот, например, как записывалось
число 38 784: XXXVIIIm DCCLXXXIV.
Неудобна и римская нумерация: записи длинные , умножение и деление в письменном виде производить невозможно.
Слайд 16
Алфавитная нумерация
Было время, когда буквами пользовались и
в качестве цифр, а чтобы отличить цифры от букв,
над буквами ставили особый знак – «титло». Такая нумерация называется алфавитной.
Слайд 17
Как считали на Руси?
В древней Руси
так же была принята алфавитная система записи чисел.
Большим
событием на Руси было введение Петром I в 1708 году гражданского шрифта и проведение реформы орфографии: ряд букв был изъят из алфавита. При Петре I вводятся арабские цифры для числового обозначения вместо обозначения их буквами.
Слайд 18
Первые счетные приборы
Пальцы человека были не только
первым счетным прибором, но и первой вычислительной машиной. Сохранились
многочисленные свидетельства о счете и вычислениях с помощью пальцев рук.
Слайд 19
Первые счётные приборы
У Древних Египтян существовала счетная доска
– абак, в отделения которой укладывались камешки, обозначающие единицы,
десятки, сотни. Из Египта абак был завезён в Грецию , а затем в Россию.
Древнеегипетский абак
Русские счеты
«Суан-пан»
(китайские счеты)
Серобян
(японские счеты)
Слайд 20
Русские счеты
На Руси во времена Ивана III были
изобретены счеты. Первая их форма – дощаный счет- представляла
собой доску или рамку с шариками, нанизанными на шнурки. На ней выполнялись четыре арифметических действия с натуральными и дробными числами.
Русские счеты
Слайд 21
Первые счетные приборы
По приговору инквизиции счетную машину
(машина для сложения)профессора Тюбингенского университета Вильгельма Шиккарда (1592-1635)
сожгли, и до нас дошли лишь чертежи этого замечательного приспособления.
Слайд 22
Первые счетные приборы
Через четыре года
после смерти
Шиккарда великий
французкий ученый
Блез Паскаль (1623-1662) создал счетную машину новой конструкции.
Слайд 23
Первые счетные приборы
Суммирующая машина французского ученого и изобретателя
Клода Перро (1613-1688) – рабдологический абак. Идеи Перро нашли
применение в ряде простых и надежных вычислительных приборов.
Рабдология – наука выполнения арифметических операций с помощью маленьких палочек с цифрами.
Слайд 24
Метод решетки
Выдающийся арабский математик и астроном Абу Абдалах
Мухаммед Бен Мусса аль - Хорезми в своей «Книге об
индийском счете» описал способ, придуманный в Древней Индии, а позже названный «методом решётки»
Слайд 25
Палочки Непера
Способ умножения решеткой положен в основу
счетного прибора, описанного шотландским математиком Джоном Непером в 1617
году.
Слайд 26
Джон Непер
«Некий шотландский барон, имени которого я не
запомнил, выступил с блестящим достижением: он каждую задачу на
умножение и деление превращает в чистое сложение и вычитание...»
Иоганн Кеплер
Слайд 27
Джон Непер
Джон Непер - шотландский барон, потомок воинствующего
рода, математик, изобретатель, инженер.
Родился в 1550 году в
замке Мерчистон близ Эдинбурга, там же и умер 4 апреля 1617 года. Учился он в Сент-Эндрюсском университете, куда поступил в 1593 году. Непер совершил путешествие по Германии, Франции и Италии, из которого вернулся на родину в 1571 году.
Поселившись в своём родном замке, он уже никогда не оставлял Шотландии.
Мерчистон,
родовой замок Непера
Слайд 28
Счетные палочки Джона Непера
Прибор представлял собой набор прямоугольных
пластин (палочек),
в который входили:
палочки с результатами умножения всех
чисел от 0 до 9 на числа от 0 до 9;
сверху каждой палочки наносилось число от 0 до 9 (на рисунке справа показаны девять таких палочек).
Результат умножения на палочках представлен двумя цифрами (в том числе начальным нулем), разделенными наклонной чертой;
одна палочка с нанесенными на нее цифрами от 1 до 9 (указатель строк)
Слайд 29
Умножение на палочках Непера: 3679135
1. Палочки, соответствующие
значениям каждого разряда множимого, выкладываются в ряд так, чтобы
цифры сверху каждой палочки составляли множимое.
Слайд 30
Умножение на палочках Непера: 3679135
2. Слева прикладывается
палочка – указатель строк, по которой выбирают строки, соответствующие
разрядам множителя. Для умножения, например, на 1 рассматриваются соответствующие строки на палочках с цифрами 3, 6, 7 и 9
Слайд 31
Умножение на палочках Непера: 3679135
3. Результат умножения числа
3679на 1:
Результат :
3679
0
Последняя цифра произведения
Слайд 32
Умножение на палочках Непера: 3679135
4. Умножение 3679 на
3
0
Последняя цифра произведения
Результат :
7
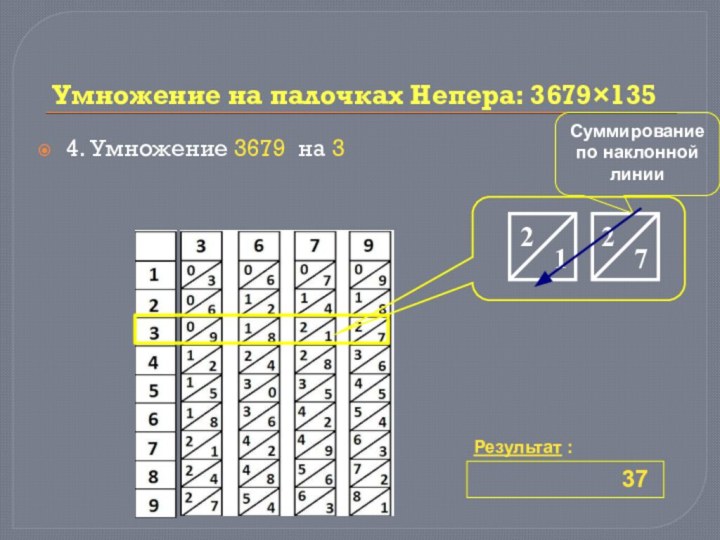
Слайд 33
Умножение на палочках Непера: 3679135
4. Умножение 3679 на
3
Результат :
37
Суммирование по наклонной линии
Слайд 34
Умножение на палочках Непера: 3679135
4. Умножение 3679 на
3
Результат :
037
Суммирование по наклонной линии
8 + 2 = 10
Перенос
в старший
разряд
Слайд 35
Умножение на палочках Непера: 3679135
4. Умножение 3679 на
3
Результат :
1037
Суммирование
по наклонной
линии
9 + 2 = 11
Перенос
в старший
разряд
Слайд 36
Умножение на палочках Непера: 3679135
4. Умножение 3679 на
3
Результат :
11037
Первая цифра произведения
0 + 1 = 1
Слайд 37
Умножение на палочках Непера: 3679135
5. Если множитель являлся
многозначным, то результаты, полученные для каждой строки (для каждой
цифры множителя), складывались между собой с учетом порядка разрядов.
3 6 7 9
1 1 0 3 7
+
1 8 3 9 5
+
4 9 6 6 6 5
Слайд 38
Логарифмы
В 1614 году шотландский математик-любитель Джон Непер опубликовал
на латинском языке сочинение под названием «Описание удивительной таблицы
логарифмов». В нём было краткое описание логарифмов и их свойств, а также
8-значные таблицы логарифмов синусов, косинусов и тангенсов, с шагом 1'.
Слайд 39
Логарифмы
На основе таблицы Непера в 1623 году для
упрощения вычислений была изобретена первая логарифмическая линейка
Слайд 40
Гидравлический винтовой насос
Непер изобрёл также гидравлический винтовой насос
оригинальной конструкции для выкачивания воды из угольных шахт, который
запатентовал в 1597 году.
Слайд 41
«Секретные изобретения»
Джона Непера
Зеркало для сжигания вражеских кораблей,
собирающее солнечные лучи в точку на любом заданном расстоянии
Слайд 42
«Секретные изобретения»
Джона Непера
Устройство для плавания под водой
с ныряльщиками, различными приспособлениями и военными хитростями для нанесения
вреда врагу
Слайд 43
«Секретные изобретения»
Джона Непера
Круглую колесницу,
непробиваемую
выстрелами из сдвоенного мушкета и движимую теми, кто находится
внутри
Слайд 44
«Секретные изобретения»
Джона Непера
Орудие, при выстреле из которого
ядро летит не по прямой линии, поражает лишь то,
что случайно окажется на его пути, и движется, рыская, над поверхностью целого заданного района, не покидает его до тех пор, пока не израсходует свою силу.
Слайд 45
Заключение
Работая над проектом, мы узнали:
когда люди научились считать;
когда
возникли современные математические символы;
как считали на Руси;
когда появились первые
счетные приборы.
В ходе работы мы создали в классе мини-музей счетных приборов, в который включили иллюстративные материалы о вычислительных приборах, изготовили палочки Непера. Собранным материалом мы поделились со своими одноклассниками. Думаем, что это их заинтересовало и расширило их математический кругозор.
Слайд 46
Сколько существует счет, столько существует интерес людей
к быстрому вычислению. Для этого люди с древнейших времен
придумывали самые разнообразные вычислительные приборы для упрощения и ускорения счета. Мы надеемся, что учеников заинтересовала данная работа и они продолжат изучать эту тему , возможно они придумают такие приборы для вычисления, которые упростят нашу жизнь.
Слайд 47
Математика – вокруг нас
Однажды знаменитый немецкий математик
Г. Лейбниц сказал о том, что без знания прошлого
не понять настоящего. Надеюсь, что наша работа пробудит интерес и к истории, и к математике , расширит кругозор , повысит эрудицию. Мир полон тайн и загадок. Но разгадать их могут только пытливые и любознательные.