Презентация на тему по математике на тему Многогранники

называются диагоналями.
Многогранником
называется тело,
поверхность которого
состоит из конечного

числа многоугольников,
называемых гранями.

Стороны и вершины этих многоугольников
называются ребрами и вершинами.

которого
состоит из шести параллелограммов
Параллелепипед называется прямоугольным, если все

его грани прямоугольники

Куб

Прямоугольный параллелепипед

Параллелепипед

многоугольников и параллелограммов, имеющих общие стороны с каждым из

оснований.

вы
с
ота

п
р
я
м
а
я

н
а
к
л
о
н
н
а
я

Призма

Два равных многоугольника называют основаниями призмы

Параллелограммы называют
боковыми гранями призмы

Перпендикуляр, проведенный из вершины одного
основания к плоскости другого основания называют
высотой.

поверхности прямой
призмы равна произведению периметра основания
на высоту.
Sбок.

= ah + ah +bh + bh =
= h( 2a + 2b) = Ph

Sполн. =

имеющих общую вершину
Многоугольник называют основанием пирамиды
Треугольники называют боковыми гранями
Общую

вершину называют вершиной пирамиды

Перпендикуляр РН называют высотой

Sбок. + Sосн.

Н

Р

Пирамида

Sполн. =

РЕ называют апофемой
Теорема: Площадь боковой поверхности правильной
пирамиды

равна половине произведения периметра
основания на апофему

Р

Е

Правильная пирамида

Боковые ребра равны

Боковые грани – равные равнобедренные треугольники

Основание высоты совпадает
с центром вписанной или
описанной окружности

правильной
усеченной пирамиды равна половине произведения
полусуммы периметров оснований

на апофему

Каждая его вершина является вершиной трёх треугольников. Следовательно, сумма

плоских углов при каждой вершине равна 180º.

Рис. 1

является вершиной четырёх треугольников. Следовательно, сумма плоских углов при

каждой вершине 240º.

Правильный октаэдр

Рис. 2

икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов

при каждой вершине равна 300º.

Рис. 3

куба является вершиной трёх квадратов. Следовательно, сумма плоских углов

при каждой вершине равна 270º.

Куб (гексаэдр)

Рис. 4

вершина додекаэдра является вершиной трёх правильных пятиугольников. Следовательно, сумма

плоских углов при каждой вершине равна 324º.

Рис. 5

граней:
«эдра» − грань;
«тетра» − 4;
«гекса» − 6;
«окта»

− 8;
«икоса» − 20;
«додека» − 12.

Названия многогранников

Платоновыми телами, поскольку они занимают видное место в философской

картине мира, разработанной великим мыслителем Древней Греции Платоном (ок. 428 – ок. 348 до н.э.).
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени.
Икосаэдр – как самый обтекаемый – воду.
Куб – самая устойчивая из фигур – землю.
Октаэдр – воздух.
В наше время эту систему можно сравнить с четырьмя состояниями вещества – твёрдым, жидким, газообразным и пламенным.
Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
Это была одна из первых попыток ввести в науку идею систематизации.

Правильные многогранники в философской картине мира Платона

что существует связь между пятью правильными многогранниками и шестью

открытыми к тому времени планетами Солнечной системы.
Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, к который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия.
Такая модель Солнечной системы (рис. 6) получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта.
Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних расстояний от Солнца.

Модель Солнечной
системы И. Кеплера

Рис. 6

о связи правильных многогранников с гармоничным устройством мира и

в наше время нашли своё продолжение в интересной научной гипотезе, которую в начале 80-х гг. высказали московские инженеры В. Макаров и В. Морозов. Они считают, что ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете. Лучи этого кристалла, а точнее, его силовое поле, обуславливают икосаэдро-додекаэдровую структуру Земли (рис. 7). Она проявляется в том, что в земной коре как бы проступают проекции вписанных в земной шар правильных многогранников: икосаэдра и додекаэдра.
Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник.
Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.

Икосаэдро-
додекаэдровая
структура Земли

Икосаэдро-додекаэдровая
структура Земли

Рис. 7

числу рёбер, увеличенному на 2.
Г + В =

Р + 2

Формула Эйлера

Число граней плюс число вершин минус число рёбер
в любом многограннике равно 2.
Г + В − Р = 2

ребер = 2.
4
4
6
8
6
12
20
12
30
12
20
30
6
8
12

додекаэдра

изобразил И. Христа со своими учениками на фоне огромного

прозрачного додекаэдра. Учёным достаточно хорошо изучены правильные выпуклые многогранники, доказано, что существует всего пять видов таких многогранников, но сам ли человек их придумал? Скорее всего – нет, он «подсмотрел» их у природы.

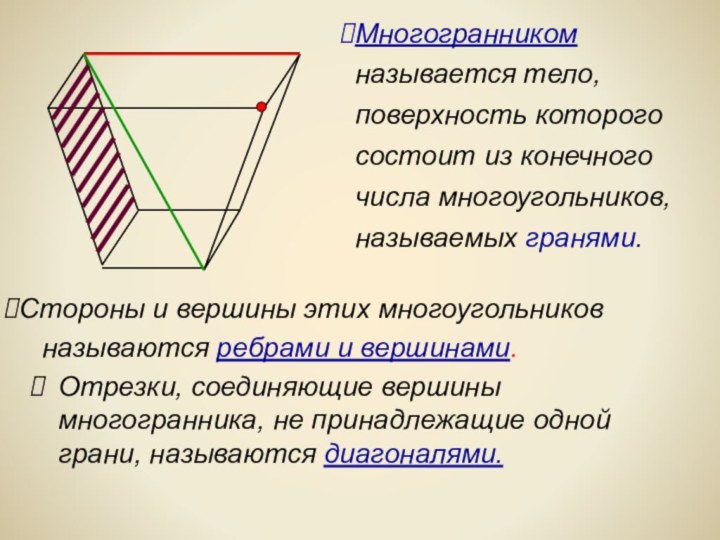
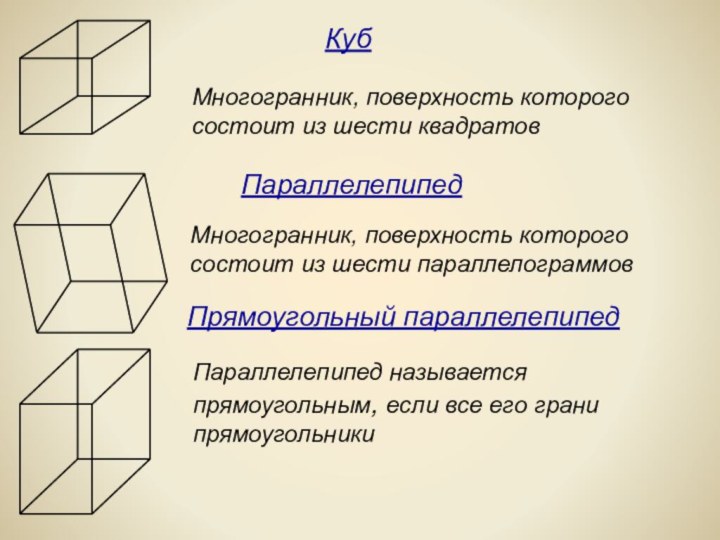
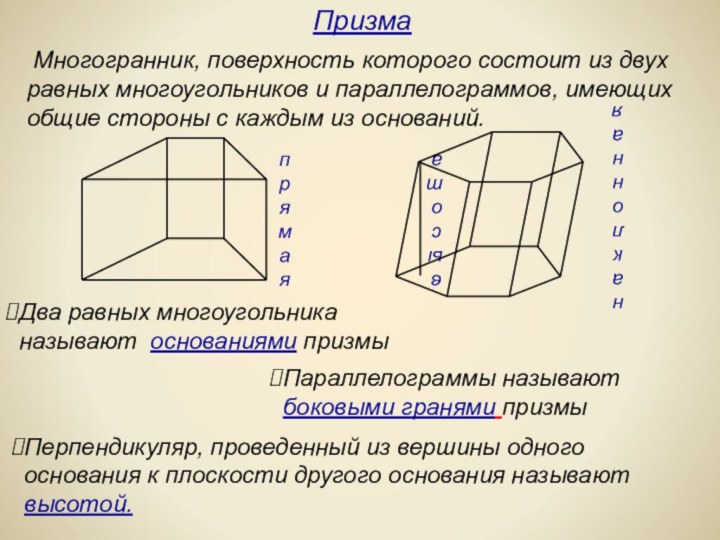
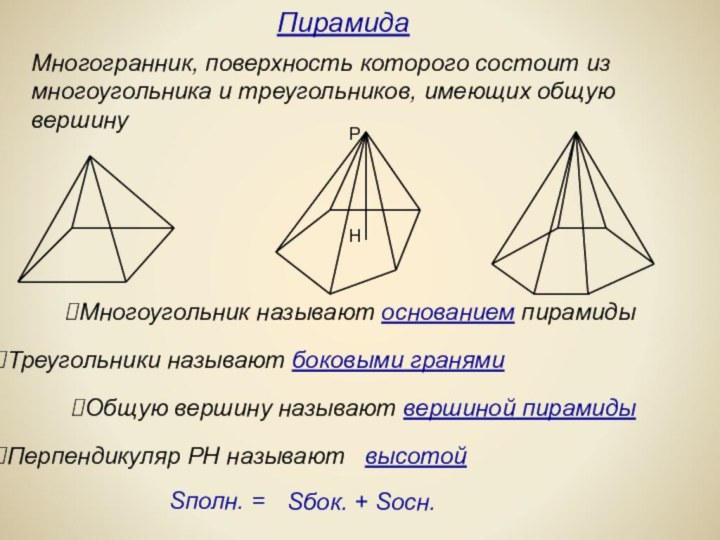
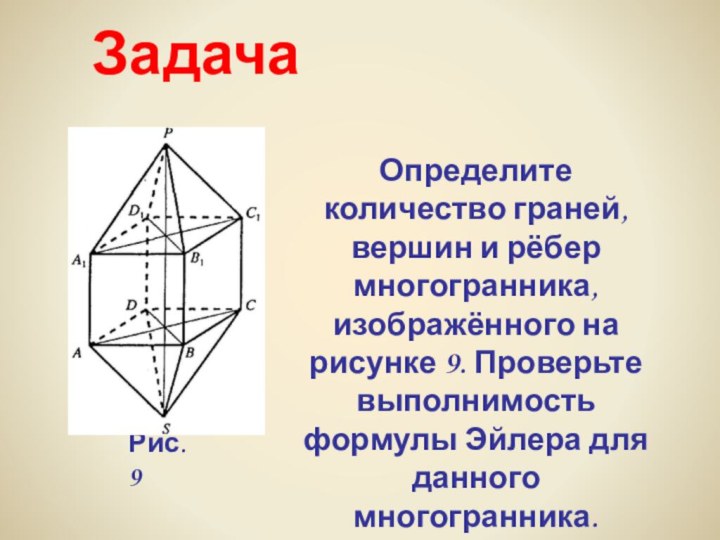
многогранники встречаются в живой природе. Например, скелет одноклеточного организма

феодарии (Circjgjnia icosahtdra) по форме напоминает икосаэдр (рис. 8).
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется. Подтверждением тому служит форма некоторых кристаллов.
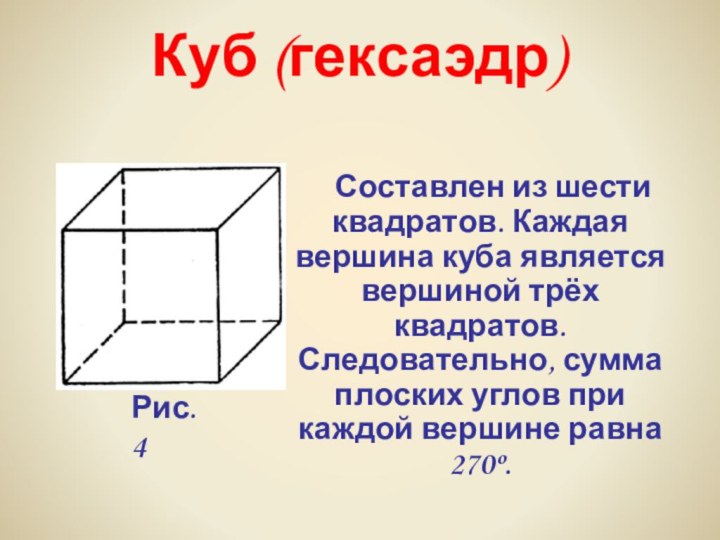
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.
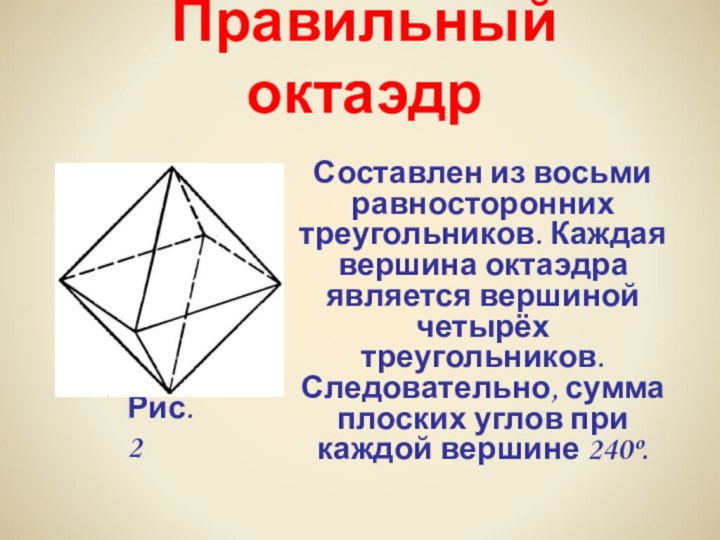
При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых имеет форму правильного октаэдра.
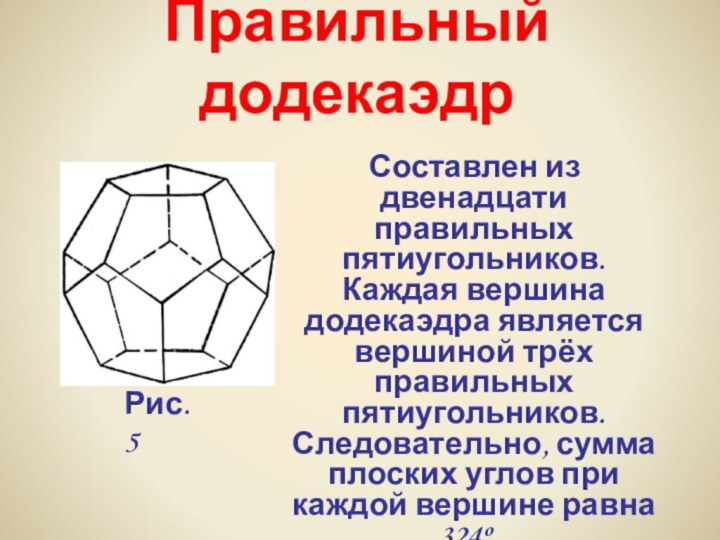
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.

Феодария
(Circjgjnia icosahtdra)

Рис. 8

на рисунке 9. Проверьте выполнимость формулы Эйлера для данного

многогранника.

Задача

Рис. 9

геометрических фигур, но и пути познания природной гармонии.
Вывод: