- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике. Пропорции вокруг нас. 6 кл.
Содержание
- 2. Цели:1.Познакомиться с историей возникновения пропорции.2.Рассмотреть применение пропорции
- 3. В переводе с латинского proportio и означает
- 4. Ещё в древней Греции математики использовали такой
- 5. Давайте поиграем! Смысловые пропорции Суть задания в
- 6. В Вавилоне с помощью пропорций рисовали планы древних городов.
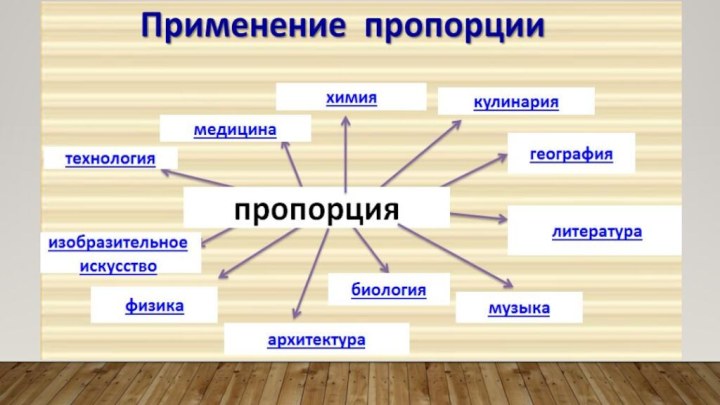
- 7. Математика применяется практически во всех сферах жизни
- 9. Архитектура При
- 10. Золотое сечение Золотое сечение
- 11. Принято считать,
- 12. Задачи на пропорции. На строительство дома идет
- 13. КУЛИНАРИЯ Когда
- 14. Задачи на пропорции. Для
- 15. МЕДИЦИНА В медицинской
- 16. Отношения
- 17. Задачи на пропорции. Для лекарственного отвара ромашки
- 18. ХимияЗаслуженное место заняла теория пропорций при решении
- 19. В химии
- 20. Задачи на пропорции.В 4 л воды растворили 100 г соли. Какова концентрация полученного раствора?
- 21. ТехнологияРазмеры элементов кукольного фартука отличаются от соответствующих
- 22. Когда мы хотим сшить какую-либо вещь меньшего
- 23. Задачи на пропорции.Краеобметочная машина 1 м ткани
- 24. Физика С глубокой
- 25. Задачи на пропорции. В городе
- 26. Моделирование Пропорция применяется при моделированииВсе пропорции сохранены!АвтомобильУменьшенная модель
- 27. Задачи на пропорции. Длина модели автомашины
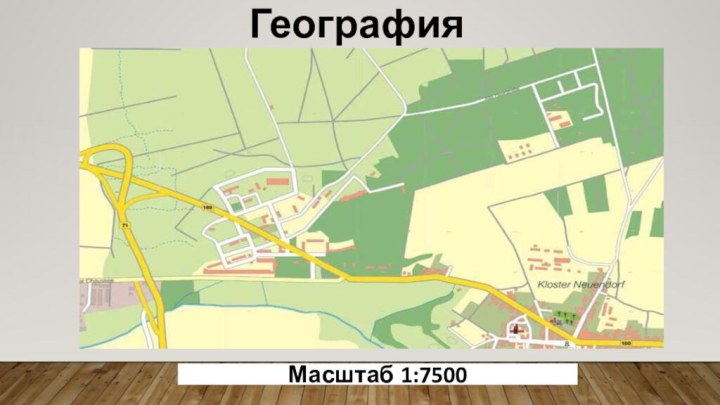
- 28. ГеографияМасштаб 1:7500
- 29. Задачи на пропорции. Найдите расстояние от Москвы
- 30. ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО Красота предмета образуется пропорциями,
- 31. В классике изобразительного
- 32. "Золотая пропорция" -
- 33. Золотая пропорция в произведениях изобразительного искусства.
- 34. ЗОЛОТОЕ СЕЧЕНИЕ В ФОТОГРАФИИ
- 35. Биология Это же явление
- 36. Золотое число наблюдается в пропорциях гармонично развитого
- 37. Музыка 1:2 – октава
- 38. В
- 39. Литература Литература входит
- 40. Аристотель заметил,
- 41. В. Брюсов, покоренный миром пропорции, писал: Вам
- 42. Скачать презентацию
- 43. Похожие презентации
Цели:1.Познакомиться с историей возникновения пропорции.2.Рассмотреть применение пропорции в жизни.3.Исследовать применение пропорций в области математики, живописи, архитектуры, медицины.







































Слайд 2
Цели:
1.Познакомиться с историей возникновения пропорции.
2.Рассмотреть применение пропорции в
жизни.
Слайд 3
В переводе с латинского proportio и означает «соразмерность».
Учение
о пропорциях успешно развивалось в 4 веке до н.
э. в Древней Греции. Пифагор и его ученики много внимания уделяли изучению пропорций. С пропорциями они связывали мысли о порядке и красоте в природе.Пропорции используют с древности при решении разных задач в математике.
Из истории
Слайд 4 Ещё в древней Греции математики использовали такой аппарат,
как ПРОПОРЦИЯ.
Пропорцией называют равенство отношений двух
чисел или величин.
Слайд 5
Давайте поиграем!
Смысловые пропорции
Суть задания в том, чтобы
понять, каковы отношения между членами пропорции, и найти недостающее
слово. Пропорции могут быть построены на сходстве или противоположности, на связи по типу «часть-целое», «причина-следствие», «форма-содержание» и т.д.Решаем смысловую пропорцию, например, такую:
добро / зло = свет/ ?
лампа / свет = радио /
тигр / кошка = волк /
лицо / портрет = природа /
Слайд 7 Математика применяется практически во всех сферах жизни человека.
И в повседневной жизни мы используем математические
навыки, в том числе и пропорцию.
Слайд 9
Архитектура
При постройке
храма в честь богини Дианы римляне взяли пропорцию, которой
отличаются стройные женщины: толщина колоны составила лишь 1/8 ее высоты.
Слайд 10
Золотое сечение
Золотое сечение –
это такое пропорциональное деление отрезка на неравные части, при
котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему.Слайд 11 Принято считать, что
понятие о золотом делении ввел в научный обиход Пифагор,
древнегреческий философ и математик (VI в. до н.э.).
Слайд 12
Задачи на пропорции.
На строительство дома идет 4
тыс. штук кирпича. Сколько тысяч штук кирпича необходимо для
строительства 15 таких же домов.
Слайд 13
КУЛИНАРИЯ
Когда мы
готовим какое-либо блюдо, мы стараемся использовать то количество продуктов,
которое указано в поварской книге. Это делается для того, чтобы не испортить блюдо.
Слайд 14
Задачи на пропорции.
Для приготовления
варенья из 2 кг крыжовника необходимо 3 кг сахара.
Сколько кг сахара необходимо для приготовления варенья из 10 кг крыжовника.
Слайд 15
МЕДИЦИНА
В медицинской практике
врачи следят за тем, сколько и когда надо давать
лекарства больному. В правильных дозах лекарство даёт лечебный эффект, в меньших – оно бесполезно, а в больших – приносит вред. При изготовлении лекарств тоже соблюдаются пропорции. Здесь необходима точность, так как при нарушении пропорций, составляющих лекарство ингредиентов, может получиться не лекарство, а яд.Слайд 16 Отношения и
пропорции используется также в аптеках при изготовлении лекарств и
лечебных напитков. Чтобы изготовить лекарственный препарат надо точно знать, сколько частей приходится на какую-либо часть.Мазь Тигровая
Масло гвоздичное ______ 0,1
Масло эвкалиптовое ____ 1
Парафин _____________ 3,05
Ментол ______________ 1,8
Камфара ______________ 1
Вазелин _______________ 3,05
Слайд 17
Задачи на пропорции.
Для лекарственного отвара ромашки на
100 г кипятка необходимо 20 г сухой ромашки. Сколько
г ромашки необходимо для 500г отвара?
Слайд 18
Химия
Заслуженное место заняла теория пропорций при решении задач
по химии.
Пример задачи.
Какова процентная
концентрация раствора, полученного растворением
5 г поваренной соли в 45 г воды?Слайд 19 В химии точные
весовые пропорции различных веществ при соединении дают возможность получения
нового вещества.
Слайд 20
Задачи на пропорции.
В 4 л воды растворили
100
г соли.
Какова концентрация
полученного раствора?
Слайд 21
Технология
Размеры элементов кукольного фартука отличаются от соответствующих размеров
фартука девушки в одно и тоже число раз.
Рост девушки-160
смРост куклы-50 см
Слайд 22 Когда мы хотим сшить какую-либо вещь меньшего или
большего размера, мы уменьшаем или увеличиваем выкройку пропорционально размеру.
Слайд 23
Задачи на пропорции.
Краеобметочная машина 1 м ткани обрабатывает
за 4 мин. Сколько метров можно обметать за 6
мин?
Слайд 24
Физика
С глубокой древности
люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели,
тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.
Слайд 25
Задачи на пропорции.
В городе Жуковском
на авиа-шоу МАКС проходят показательные полёты самолётов. Такому самолёту-истребителю,
как МИГ-29 на 3 часа полётов требуется около 8 тонн керосина. Сколько тонн керосина потребуется МИГ-29 на 7 часов полётов?
Слайд 26
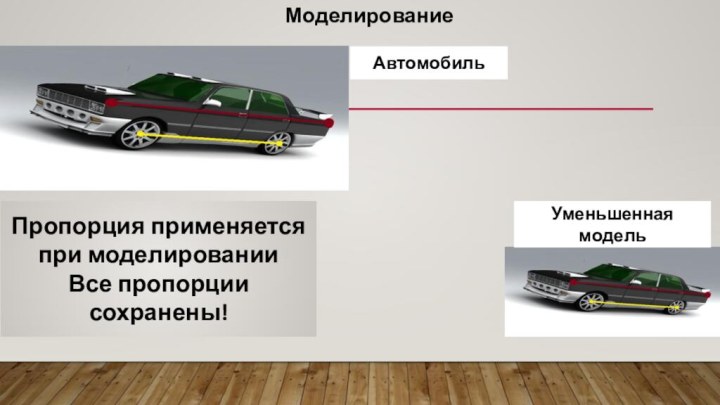
Моделирование
Пропорция применяется при моделировании
Все пропорции сохранены!
Автомобиль
Уменьшенная модель
Слайд 27
Задачи на пропорции.
Длина модели автомашины 42мм.
Какова
длина автомобиля, если размеры его уменьшены в 100 раз?
Слайд 29
Задачи на пропорции.
Найдите расстояние от Москвы до
Северного полюса, если на карте это расстояние – 5
см,если М = 1 : 100000000
Слайд 30
ИЗОБРАЗИТЕЛЬНОЕ ИСКУССТВО
Красота предмета образуется пропорциями, становясь
строгой соразмерностью, гармонией всех частей, такой, что ни прибавить,
ни убавить ничего нельзя, и все детали, части должны взаимно соответствовать друг другу.Слайд 31 В классике изобразительного искусства
на протяжении многих веков прослеживается приём построения пропорции, называемый
золотым сечением, или золотым числом (этот термин ввел Леонардо да Винчи).Слайд 32 "Золотая пропорция" - это
понятие математическое и ее изучение – это прежде всего
задача науки. Но она же является критерием гармонии и красоты, а это уже категория искусства и эстетики, которая изучает гармонию и красоту с математической точки зрения.
Слайд 35
Биология
Это же явление наблюдается
и в иных конструкциях природы: в спиралях моллюсков, в
венчиках цветков и ещё во многих знакомых нам вещах, например, расположение листьев на побеге тоже подчиняется золотому числу!Слайд 36 Золотое число наблюдается в пропорциях гармонично развитого человека:
длина головы делит в золотом сечении расстояние от талии
до макушки.Кроме этого есть и еще несколько основных золотых пропорции нашего тела:
расстояние от кончиков пальцев до запястья и от запястья до локтя равно 1:1.618
расстояние от уровня плеча до макушки головы и размера головы равно 1:1.618
расстояние от точки пупа до макушки головы и от уровня плеча до макушки головы
равно 1:1.618
расстояние точки пупа до коленей и от коленей до ступней
равно 1:1.618
расстояние от кончика подбородка до кончика верхней губы и от кончика верхней губы до ноздрей
равно 1:1.618
расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки
равно 1:1.618
расстояние от кончика подбородка до верхней линии бровей и от верхней линии бровей до макушки
равно 1:1.618
Слайд 38 В основе
музыкальных произведений лежат четкие соотношения, описываемые количественными законами.
Г. Лейбниц писал: «Музыка – это радость души, которая вычисляет,
сама того не зная».
Слайд 39
Литература
Литература входит в
ту же область творчества, что и музыка и изобразительное
искусство. Так, значит, и здесь должна быть связь с математикой? Ясно, что эту связь необходимо искать в поэзии. В математике существует ряд исследований, в частности академика А.Колмогорова и его учеников, посвященных анализу русского стиха.Слайд 40 Аристотель заметил, что
сравнения и тропы в поэзии создаются по правилам отношений
существующими между членами пропорции.По примеру Аристотеля, доктор философии А. Сухотин, на основании основного свойства пропорции рассмотрел поэтическое выражение:
«Что старость для жизни, то вечер для дня».
Слайд 41
В. Брюсов, покоренный миром пропорции, писал:
Вам поклоняюсь,
вас желаю числа!
Свободные бесплотные как тени,
Вы радугой
связующей повислиК раздумиям с вершины вдохновенья.