- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение задач обязательной части ГИА по геометрии
Содержание
- 2. Математика является одним из наиболее важных предметов
- 3. 1. Структура ГИА 2014.2. Типичные ошибки.3. Основные
- 4. ГИА по математике в 2013 году (235
- 5. Работа состоит из трех модулей (необходимо
- 6. Три формы заданий 1 частиВыбор одного ответа
- 7. Назначение второй части работы ГИА 1. Дифференцировать
- 8. Типичные ошибкиНевнимательное чтение условия и вопроса задания
- 9. Основные направления в работе:Совершенствование у учащихся
- 10. Модуль «Геометрия» содержит 8 заданий: в части
- 11. Модуль «Геометрия» содержит 8 заданий: в части
- 12. Ответ: 70 Повторение (2) Модуль «ГЕОМЕТРИЯ» № 9 (1)
- 13. ПовторениеВ равнобедренном треугольнике углы при основании равныВ треугольнике сумма углов равна 180°
- 14. Ответ: 6. Повторение (3)∠ВСА = 180° - 57° - 117°=6°Модуль «ГЕОМЕТРИЯ» № 9 (2)
- 15. ПовторениеВнешний угол треугольника – это угол, смежный
- 16. Ответ: 111. Повторение (3)Модуль «ГЕОМЕТРИЯ» № 9 (3)
- 17. ПовторениеВ равнобедренном треугольнике углы при основании равныБиссектриса
- 18. Ответ: 134. Один из углов параллелограмма на 46°
- 19. ПовторениеПараллелограмм – это четырехугольник, у которого противоположные
- 20. Ответ: 108. Найти больший угол параллелограмма АВСD.Повторение (2) ∠DCВ=∠АCD+∠АСВ=23°+49°=72°∠С+∠В=180°∠В=180°-∠В=180°-72°=108°Модуль «ГЕОМЕТРИЯ» № 9 (5)
- 21. ПовторениеЕсли угол разделен на части, то его
- 22. Ответ: 126.Повторение (2) Углы ромба относятся как
- 23. ПовторениеВ ромбе противоположные стороны параллельныЕсли две параллельные
- 24. Ответ: 124.Повторение (2) Разность противолежащих углов трапеции
- 25. ПовторениеВ равнобедренном треугольнике углы при основании равны.Сумма углов, прилежащих боковой стороне трапеции равна 180°.
- 26. Модуль «ГЕОМЕТРИЯ» №10 (1)Повторение (2)Ответ: 4.Найти АС.В С А 5 ⇒ ⇒ По теореме Пифагора
- 27. ПовторениеКосинус острого угла прямоугольного треугольника равен отношению
- 28. Модуль «ГЕОМЕТРИЯ» №10 (2)Повторение (2)Ответ: 17.Найти АВ.В С А 15 ⇒ ⇒ По теореме Пифагора
- 29. ПовторениеТангенс острого угла прямоугольного треугольника равен отношению
- 30. Модуль «ГЕОМЕТРИЯ» №10 (3)Повторение (3)Ответ: 52.Найти АВ.В
- 31. ПовторениеВысота в равнобедренном треугольнике, проведенная к основанию,
- 32. Модуль «ГЕОМЕТРИЯ» №10 (4)Повторение (2)Ответ: 117.Найти CH.В
- 33. ПовторениеВысота в равнобедренном треугольнике, проведенная к основанию,
- 34. Модуль «ГЕОМЕТРИЯ» №10 (5)Повторение (3)Ответ: 37,5.Найти AB.В
- 35. ПовторениеВысота в прямоугольном треугольнике, проведенная к основанию
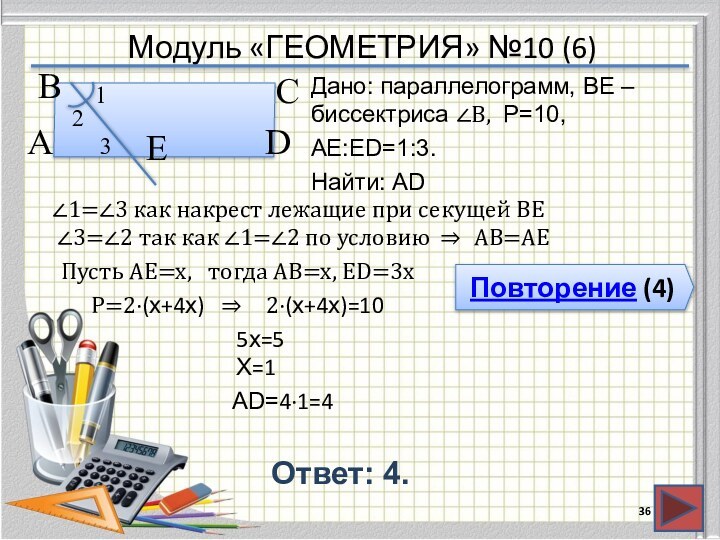
- 36. Модуль «ГЕОМЕТРИЯ» №10 (6)Повторение (4)Ответ: 4.Дано: параллелограмм,
- 37. ПовторениеБиссектриса – это луч, который делит угол
- 38. Модуль «ГЕОМЕТРИЯ» №10 (7)Повторение (3)Ответ: 94.АВСD –
- 39. ПовторениеЕсли гипотенуза и катет одного прямоугольного треугольника
- 40. Модуль «ГЕОМЕТРИЯ» №11 (1)Повторение (1)Ответ: 6.Найти площадь треугольника.В С А 8 3 30⁰
- 41. ПовторениеПлощадь треугольника равна половине произведения двух сторон на синус угла между ними
- 42. Модуль «ГЕОМЕТРИЯ» №11 (2)Повторение (2)Ответ: 13,5.АВ=3CH.Найти площадь треугольника АВСВ С А 3 H АВ=3CH=3∙3=9
- 43. ПовторениеВысота треугольника – это отрезок, проведенный из
- 44. Модуль «ГЕОМЕТРИЯ» №11 (3)Повторение (2)Ответ:
- 45. ПовторениеПлощадь параллелограмма равна произведению двух сторон на
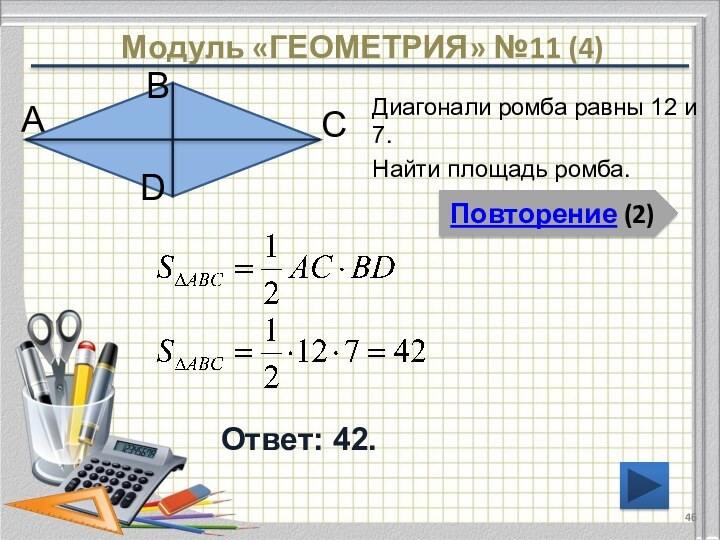
- 46. Модуль «ГЕОМЕТРИЯ» №11 (4)Повторение (2)Ответ: 42.Диагонали ромба
- 47. ПовторениеПлощадь ромба равна половине произведения его диагоналейРомб – это параллелограмм с равными сторонами
- 48. Модуль «ГЕОМЕТРИЯ» №11 (5)Повторение (5)Ответ:
- 49. ПовторениеДиагонали прямоугольника равны и делятся точкой пересечения
- 50. Модуль «ГЕОМЕТРИЯ» №11 (6)Повторение (2)Ответ: 73,5.ABCD –
- 51. ПовторениеПлощадь трапеции равна произведению полусуммы оснований на высотуТрапеция – это четырехугольник, две стороны которого параллельны
- 52. Модуль «ГЕОМЕТРИЯ» №11 (7)Повторение (4)Ответ:
- 53. ПовторениеПлощадь трапеции равна произведению полусуммы оснований на
- 54. Модуль «ГЕОМЕТРИЯ» №12 (1)Повторение (3)Ответ: 45.Найти угол
- 55. Повторение (подсказка)Треугольник называется прямоугольным, если в нем
- 56. Модуль «ГЕОМЕТРИЯ» №12 (2)Повторение (4)Ответ:135 .Найти угол
- 57. Повторение (подсказка)В равнобедренном треугольнике углы при основании
- 58. Модуль «ГЕОМЕТРИЯ» №12 (3)Повторение (2)Ответ: 0,8.Найти синус
- 59. Повторение (подсказка)Синусом острого угла прямоугольного треугольника называется
- 60. Модуль «ГЕОМЕТРИЯ» №12 (4)Повторение (2)Ответ: 0,2.Найти косинус
- 61. Повторение (подсказка)Косинусом острого угла прямоугольного треугольника называется
- 62. Модуль «ГЕОМЕТРИЯ» №12 (5)Повторение (2)Ответ: 2,4.Найти тангенс
- 63. Повторение (подсказка)Тангенсом острого угла прямоугольного треугольника называется
- 64. Модуль «ГЕОМЕТРИЯ» №12 (6)Повторение (3)Ответ: 1.Повторение (3)Найти
- 65. Повторение (подсказка)В равнобедренном треугольнике углы при основании
- 66. Модуль «ГЕОМЕТРИЯ» №12 (7)Повторение (2)Ответ: 0,6.Найти косинус
- 67. Повторение (подсказка)Косинусом острого угла прямоугольного треугольника называется
- 68. Модуль «ГЕОМЕТРИЯ» №13 (1)Повторение(3)Ответ: 23.Укажите номера верных
- 69. Повторение (подсказка)Сформулируйте аксиому о взаимном расположении прямой
- 70. Модуль «ГЕОМЕТРИЯ» №13 (2)Повторение(2)Ответ: 2.Укажите номера верных
- 71. Повторение (подсказка)Сформулируйте свойство вертикальных углов.Сколько прямых можно
- 72. Модуль «ГЕОМЕТРИЯ» №13 (3)Повторение(3)Ответ: 3.Укажите номера верных
- 73. Повторение (подсказка)Как могут взаимно располагаться три прямых
- 74. Модуль «ГЕОМЕТРИЯ» №13 (4)Повторение(2)Ответ: 1.Укажите номера верных
- 75. Повторение (подсказка)Сформулируйте аксиому о взаимном расположении прямой
- 76. Модуль «ГЕОМЕТРИЯ» №13 (5)Повторение(2)Ответ: 13.Укажите номера верных
- 77. Повторение (подсказка)Сколько прямых можно провести через точку
- 78. Модуль «ГЕОМЕТРИЯ» №13 (6)Повторение(2)Ответ: 1.Укажите номера верных
- 79. Повторение (подсказка)Сформулируйте свойство параллельных прямых относительно соответственных
- 80. Модуль «ГЕОМЕТРИЯ» №13 (7)Повторение(3)Ответ: 3.Укажите номера верных
- 81. Повторение (подсказка)Сформулируйте признак параллельности двух прямых относительно
- 82. Рекомендации учителю1. В работе по математике и
- 83. 3. Использовать при подготовке учащихся к ГИА
- 84. 5. Математика в школе должна быть красивой,
- 85. Рекомендации ученикам: 1. Объективно
- 86. 4. Научитесь выделять и понимать главное в
- 87. Модуль «Геометрия» содержит 8 заданий: в части
- 88. Модуль «Геометрия» содержит 8 заданий: в части
- 89. Скачать презентацию
- 90. Похожие презентации























































































Слайд 2
Математика является одним из наиболее важных предметов школьного
курса.
изучения математики каждым учащимся.
Слайд 3
1. Структура ГИА 2014.
2. Типичные ошибки.
3. Основные направления
в работе.
4. Рекомендации учителям.
5. Рекомендации учащимся.
6. ЦОР по подготовке
к ГИА.Рассматриваемые вопросы:
Слайд 4
ГИА по математике в 2013 году
(235 минут)
1 часть
20
заданий базового уровня
2 часть
4 задания повышенного и 2 задания
высокого уровня
Слайд 5 Работа состоит из трех модулей (необходимо набрать не
менее 8 баллов)
Алгебра (3 балла)
Реальная математика ( 2 балла)
Геометрия
(2 балла)
Слайд 6
Три формы заданий 1 части
Выбор одного ответа из
4 предложенных вариантов
(5 заданий)
Установления соответствия между объектами двух
множеств (2 задания)
С кратким ответом
( 13 заданий)
Слайд 7
Назначение второй части работы ГИА
1. Дифференцировать хорошо
успевающих школьников по уровням подготовки.
2. Выявить потенциальный контингент профильных
классов.3 задачи по геометрии и 3 задачи по алгебре
- Расположены по нарастанию трудности.
- Все задания требуют полной записи решения и ответа.
- Методы и формы записи решения могут быть произвольными.
Содержание второй части работы ГИА
Слайд 8
Типичные ошибки
Невнимательное чтение условия и вопроса задания
Неверное
применение формул и свойств фигур при решении геометрических задач
Вычислительные
ошибки
Логические ошибки при решении текстовых задач .
Раскрытие скобок и применение формул сокращенного умножения
Слайд 9
Основные направления в работе:
Совершенствование у учащихся навыка
самостоятельного решения задач
Развитие у учащихся логического мышления; формирование познавательного
интереса, а также умения правильно излагать свои мысли
Выработка у школьников умения концентрироваться и продуктивно работать в условиях экзамена
Получение учащимися знаний в объеме, достаточном для успешного написания экзамена
Слайд 10
Модуль «Геометрия» содержит 8 заданий: в части 1
- 5 заданий, в час-
ти 2 - 3 задания.
Модуль
«Геометрия» содержит 8 заданий:в части 1 - 5 заданий, в части 2 - 3 задания.
Слайд 11
Модуль «Геометрия» содержит 8 заданий: в части 1
- 5 заданий, в час-
ти 2 - 3 задания.
Вашему
вниманию представлены тридцать пять
прототипов задач № 9, 10, 11, 12, 13
ГИА – 2013.
Задача № 9. 1Задача № 9. 1, 2Задача № 9. 1, 2, 3Задача № 9. 1, 2, 3, 4Задача № 9. 1, 2, 3, 4, 5Задача № 9. 1, 2, 3, 4, 5, 6Задача № 9. 1, 2, 3, 4, 5, 6, 7
Задача № 10. 1Задача № 10. 1, 2Задача № 10. 1, 2, 3Задача № 10. 1, 2, 3, 4Задача № 10. 1, 2, 3, 4, 5Задача № 10. 1, 2, 3, 4, 5, 6Задача № 10. 1, 2, 3, 4, 5, 6, 7
Задача № 11. 1Задача № 11. 1, 2Задача № 11. 1, 2, 3Задача № 11. 1, 2, 3, 4Задача № 11. 1, 2, 3, 4, 5Задача № 11. 1, 2, 3, 4, 5, 6Задача № 11. 1, 2, 3, 4, 5, 6, 7
Задача № 12. 1Задача № 12. 1, 2Задача № 12. 1, 2, 3Задача № 12. 1, 2, 3, 4Задача № 12. 1, 2, 3, 4, 5Задача № 12. 1, 2, 3, 4, 5, 6Задача № 12. 1, 2, 3, 4, 5, 6, 7
Задача № 13. 1Задача № 13. 1, 2Задача № 13. 1, 2, 3Задача № 13. 1, 2, 3, 4Задача № 13. 1, 2, 3, 4, 5Задача № 13. 1, 2, 3, 4, 5, 6Задача № 13. 1, 2, 3, 4, 5, 6, 7
Слайд 13
Повторение
В равнобедренном треугольнике углы при основании равны
В треугольнике
сумма углов равна 180°
Слайд 15
Повторение
Внешний угол треугольника – это угол, смежный с
углом треугольника
Сумма смежных углов углов равна 180°
В треугольнике сумма
углов равна 180°
Слайд 17
Повторение
В равнобедренном треугольнике углы при основании равны
Биссектриса –
это луч, который делит угол пополам
В треугольнике сумма углов
равна 180°
Слайд 18
Ответ: 134.
Один из углов параллелограмма на 46° больше
другого. Найти больший из них.
Повторение (2)
∠А+∠D=180°
Пусть ∠А=х°, тогда∠D=х°+46°
х+х+46=180
2х=134
х=67
∠D
=2∙67°=134°Модуль «ГЕОМЕТРИЯ» № 9 (4)
Слайд 19
Повторение
Параллелограмм – это четырехугольник, у которого противоположные стороны
параллельны.
Если две параллельные прямые пересечены третьей, то сумма внутренних
односторонних углов равна 180°
Слайд 20
Ответ: 108.
Найти больший угол параллелограмма АВСD.
Повторение (2)
∠DCВ=∠АCD+∠АСВ=23°+49°=72°
∠С+∠В=180°
∠В=180°-∠В=180°-72°=108°
Модуль
«ГЕОМЕТРИЯ» № 9 (5)
Слайд 21
Повторение
Если угол разделен на части, то его градусная
мера равна сумме градусных мер его частей.
В параллелограмме сумма
соседних углов равна 180°
Слайд 22
Ответ: 126.
Повторение (2)
Углы ромба относятся как 3:7
.
Найти больший угол.
∠1+∠2=180°
Пусть х° - одна часть, тогда∠2=3х°,
∠1=7х° 3х+7х=180
10х=180
х=18
∠1=18°∙7=126°
Модуль «ГЕОМЕТРИЯ» № 9 (6)
Слайд 23
Повторение
В ромбе противоположные стороны параллельны
Если две параллельные прямые
пересечены третьей, то сумма внутренних односторонних углов равна 180°
Слайд 24
Ответ: 124.
Повторение (2)
Разность противолежащих углов трапеции равна
68°. Найти больший угол.
∠А+∠В=180°
Если ∠А=х°, то ∠В=х°+68°
х+х+68=180
2х=180-68
х = 56
∠В=56°+68°=124°
∠В=∠С
Модуль «ГЕОМЕТРИЯ» № 9 (7)
Слайд 25
Повторение
В равнобедренном треугольнике углы при основании равны.
Сумма углов,
прилежащих боковой стороне трапеции равна 180°.
Слайд 27
Повторение
Косинус острого угла прямоугольного треугольника равен отношению прилежащего
катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов
Слайд 28
Модуль «ГЕОМЕТРИЯ» №10 (2)
Повторение (2)
Ответ: 17.
Найти АВ.
В
С
А
15
⇒
⇒
По теореме Пифагора
Слайд 29
Повторение
Тангенс острого угла прямоугольного треугольника равен отношению противолежащего
катета к прилежащему
В прямоугольном треугольнике квадрат гипотенузы равен сумме
квадратов катетов
Слайд 30
Модуль «ГЕОМЕТРИЯ» №10 (3)
Повторение (3)
Ответ: 52.
Найти АВ.
В
С
А
26
BH=HA, зн. АВ=2 AH.
H
⇒
HA=СH=26.
АВ=2 ∙26=52.
Слайд 31
Повторение
Высота в равнобедренном треугольнике, проведенная к основанию, является
и медианой
В прямоугольном треугольнике сумма острых углов равна 90⁰
Если
в треугольнике два угла равны, то такой треугольник равнобедренный
Слайд 32
Модуль «ГЕОМЕТРИЯ» №10 (4)
Повторение (2)
Ответ: 117.
Найти CH.
В
А
H
С
BH=HA, зн. АH=½ AB=
По теореме Пифагора в
∆ACH
Слайд 33
Повторение
Высота в равнобедренном треугольнике, проведенная к основанию, является
и медианой
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов
катетов
Слайд 34
Модуль «ГЕОМЕТРИЯ» №10 (5)
Повторение (3)
Ответ: 37,5.
Найти AB.
В
А
H
С
120⁰
Проведем высоту CH, получим ∆ВCH.
∠ВCH=60⁰
⇒
∠CВH=30⁰
⇒
По теореме Пифагора в ∆BCH
Слайд 35
Повторение
Высота в прямоугольном треугольнике, проведенная к основанию является
биссектрисой и медианой
В прямоугольном треугольнике катет, лежащий против угла
в 30⁰, равен половине гипотенузыВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 36
Модуль «ГЕОМЕТРИЯ» №10 (6)
Повторение (4)
Ответ: 4.
Дано: параллелограмм, BE
– биссектриса ∠B, P=10,
АЕ:ЕD=1:3.
Найти: AD
В
А
D
С
Е
1
2
3
∠1=∠3 как накрест лежащие при секущей ВЕ
∠3=∠2 так как ∠1=∠2 по условию
⇒
АВ=АЕ
Пусть АЕ=х,
тогда АВ=х, ЕD=3х
Р=2∙(х+4х)
⇒
2∙(х+4х)=10
5х=5
Х=1
AD=4∙1=4
Слайд 37
Повторение
Биссектриса – это луч, который делит угол пополам
Периметр
многоугольника – это сумма длин всех сторон многоугольника
При пересечении
двух параллельных прямых накрест лежащие углы равныЕсли два угла в треугольнике равны, то треугольник - равнобедренный
Слайд 38
Модуль «ГЕОМЕТРИЯ» №10 (7)
Повторение (3)
Ответ: 94.
АВСD – трапеция,
AH=51, HD=94
Найти среднюю линию трапеции
В
А
D
С
94
51
H
?
К
М
Проведем СЕ⍊AD, получим ∆ABH=∆CED и прямоугольник BCEH
⇒
AD=AH+HE+ЕD=
E
51+94=145
⇒
AH=ЕD=51,
BC=HE=HD-ED=94-51=43,
⇒
Слайд 39
Повторение
Если гипотенуза и катет одного прямоугольного треугольника соответственно
равны гипотенузе и катету другого треугольника, то треугольники равны
Если
отрезок точкой разделен на части, то его длина равна сумме длин его частейСредняя линия трапеции равна полусумме оснований трапеции
Слайд 41
Повторение
Площадь треугольника равна половине произведения двух сторон на
синус угла между ними
Слайд 42
Модуль «ГЕОМЕТРИЯ» №11 (2)
Повторение (2)
Ответ: 13,5.
АВ=3CH.
Найти площадь треугольника
АВС
В
С
А
3
H
АВ=3CH=3∙3=9
Слайд 43
Повторение
Высота треугольника – это отрезок, проведенный из вершины
к противоположной стороне под прямым углом
Площадь треугольника равна половине
произведения основания на высоту
Слайд 45
Повторение
Площадь параллелограмма равна произведению двух сторон на синус
угла между ними
Сумма квадратов синуса и косинуса одного и
того же угла равна единице
Слайд 46
Модуль «ГЕОМЕТРИЯ» №11 (4)
Повторение (2)
Ответ: 42.
Диагонали ромба равны
12 и 7.
Найти площадь ромба.
В
А
D
С
Слайд 47
Повторение
Площадь ромба равна половине произведения его диагоналей
Ромб –
это параллелограмм с равными сторонами
Слайд 48
Модуль «ГЕОМЕТРИЯ» №11 (5)
Повторение (5)
Ответ:
АС=10.
Найти площадь прямоугольника
В
А
D
С
60⁰
О
АО=ВО=10:2=5
В ∆АОВ, где ∠ВАО= ∠АВО=(180⁰-60⁰):2=60⁰
⇒
АВ=5
По теореме Пифагора в ∆АВD
Слайд 49
Повторение
Диагонали прямоугольника равны и делятся точкой пересечения пополам
В
равнобедренном треугольнике углы при основании равны
Если угол разбит на
части, то его градусная мера равна сумме его частейВ прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Площадь прямоугольника равна произведению соседних сторон
Слайд 50
Модуль «ГЕОМЕТРИЯ» №11 (6)
Повторение (2)
Ответ: 73,5.
ABCD – трапеция.
ВС в 2 раза меньше AD. Найти площадь трапеции
В
А
D
С
14
H
ВС=14:2=7
BC=BH=7
Слайд 51
Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Трапеция
– это четырехугольник, две стороны которого параллельны
Слайд 52
Модуль «ГЕОМЕТРИЯ» №11 (7)
Повторение (4)
Ответ:
ABCD – равнобедренная трапеция MK=8, боковая сторона
равна 5.Найти площадь трапеции.
В
А
D
С
8
135⁰
H
К
М
⇒
По теореме Пифагора в ∆АВH, где AH=BH=х
∠АВH=135⁰-90⁰=45⁰
⇒
∠ВАH= ∠АВH=45⁰
⇒
Слайд 53
Повторение
Площадь трапеции равна произведению полусуммы оснований на высоту
Средняя
линия трапеции равна полусумме оснований
Если в прямоугольном треугольнике острый
угол равен 45⁰, то и другой острый угол равен 45⁰ В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 54
Модуль «ГЕОМЕТРИЯ» №12 (1)
Повторение (3)
Ответ: 45.
Найти угол АВС
(в градусах)
В
С
А
Проведем из произвольной точки луча
ВА перпендикуляр до пересечения с лучом ВСПолучим прямоугольный равнобедренный треугольник
⇒
∠С=∠В=45⁰
по свойству острых углов прямоугольного треугольника
Слайд 55
Повторение (подсказка)
Треугольник называется прямоугольным, если в нем имеется
прямой угол
В равнобедренном треугольнике углы при основании равны
Сумма острых
углов прямоугольного треугольника равна 90⁰
Слайд 56
Модуль «ГЕОМЕТРИЯ» №12 (2)
Повторение (4)
Ответ:135 .
Найти угол АВС
(в градусах)
В
С
А
Проведем из произвольной точки
луча ВС перпендикуляр к прямой АВ до пересечения с нейD
Получим прямоугольный равнобедренный треугольник BCD
⇒
∠С=∠В=45⁰
по свойству острых углов прямоугольного треугольника
∠ABС+∠CВD=180⁰ как смежные
⇒
∠ABС=180⁰ - ∠CВD=135⁰
Слайд 57
Повторение (подсказка)
В равнобедренном треугольнике углы при основании равны
Сумма
острых углов прямоугольного треугольника равна 90⁰
Смежными углами называются углы,
у которых есть общая сторона, а две другие являются дополнительными лучамиСумма смежных углов равна 180⁰
Слайд 58
Модуль «ГЕОМЕТРИЯ» №12 (3)
Повторение (2)
Ответ: 0,8.
Найти синус угла
ВАС
В
С
А
4
3
По теореме Пифагора в
∆АВС
Слайд 59
Повторение (подсказка)
Синусом острого угла прямоугольного треугольника называется отношение
противолежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
Слайд 60
Модуль «ГЕОМЕТРИЯ» №12 (4)
Повторение (2)
Ответ: 0,2.
Найти косинус угла
ВАС
В
С
А
По теореме Пифагора в ∆АВС
Слайд 61
Повторение (подсказка)
Косинусом острого угла прямоугольного треугольника называется отношение
прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
Слайд 62
Модуль «ГЕОМЕТРИЯ» №12 (5)
Повторение (2)
Ответ: 2,4.
Найти тангенс угла
ВАС.
В
С
А
12
13
По теореме Пифагора в
∆АВС
Слайд 63
Повторение (подсказка)
Тангенсом острого угла прямоугольного треугольника называется отношение
противолежащего катета к прилежащему
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
Слайд 64
Модуль «ГЕОМЕТРИЯ» №12 (6)
Повторение (3)
Ответ: 1.
Повторение (3)
Найти тангенс
угла АВС.
В
С
А
Проведем из произвольной точки луча
ВА перпендикуляр до пересечения с лучом ВС.Получим прямоугольный равнобедренный треугольник
⇒
∠С=∠В=45⁰
по свойству острых углов прямоугольного тр-ка
Слайд 65
Повторение (подсказка)
В равнобедренном треугольнике углы при основании равны
Сумма
острых углов прямоугольного треугольника равна 90⁰
Тангенс угла в 45⁰
равен единице
Слайд 66
Модуль «ГЕОМЕТРИЯ» №12 (7)
Повторение (2)
Ответ: 0,6.
Найти косинус угла
АВС
В
С
А
Проведем перпендикуляр из такой точки луча
ВА до пересечения с лучом ВС, чтобы в катетах треугольника АВС укладывалось целое число единиц измерения.
где АВ=3, АС=4, значит по теореме Пифагора ВС=5 (Пифагоров треугольник)
В данном случае единицей измерения стала клетка.
Слайд 67
Повторение (подсказка)
Косинусом острого угла прямоугольного треугольника называется отношение
прилежащего катета к гипотенузе
В прямоугольном треугольнике квадрат гипотенузы равен
сумме квадратов катетов
Слайд 68
Модуль «ГЕОМЕТРИЯ» №13 (1)
Повторение(3)
Ответ: 23.
Укажите номера верных утверждений
1.Через
любые три различные точки плоскости можно провести единственную прямую.
2.Если угол равен 25⁰, то смежный с ним угол равен 155⁰
3.Через любую точку плоскости можно провести не менее одной прямой
да
нет
да
нет
да
нет
Слайд 69
Повторение (подсказка)
Сформулируйте аксиому о взаимном расположении прямой и
точек.
Каким свойством обладают смежные углы?
Сколько прямых можно провести через
точку на плоскости?Через любые две точки проходит прямая , и притом только одна
Сумма смежных углов равна 180°
Через точку на плоскости можно провести бесконечно много прямых.
Слайд 70
Модуль «ГЕОМЕТРИЯ» №13 (2)
Повторение(2)
Ответ: 2.
Укажите номера верных утверждений
1.Если
угол равен 56⁰, то вертикальный с ним угол равен
124⁰.2.Существует точка плоскости, через которую можно провести бесконечное количество различных прямых.
3.Через любую точку плоскости можно провести не более двух прямых.
да
нет
да
нет
да
нет
Слайд 71
Повторение (подсказка)
Сформулируйте свойство вертикальных углов.
Сколько прямых можно провести
через точку на плоскости?
Вертикальные углы равны
Через точку на плоскости
можно провести бесконечно много прямых.
Слайд 72
Модуль «ГЕОМЕТРИЯ» №13 (3)
Повторение(3)
Ответ: 3.
Укажите номера верных утверждений
1.Любые
три различные прямые проходят через одну общую точку.
2.Существует точка
плоскости, не лежащая на данной прямой, через которую нельзя провести на плоскости ни одной прямой, параллельной данной.3.Если угол равен 47⁰, то смежный с ним угол равен 133⁰.
да
нет
да
нет
да
нет
Слайд 73
Повторение (подсказка)
Как могут взаимно располагаться три прямых на
плоскости?
Сформулируйте аксиому параллельных прямых.
Сформулируйте свойство смежных углов.
Три прямых на
плоскости могут иметь одну общую точку, могут пересекаться попарно, могут и не иметь общих точекЧерез точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Сумма смежных углов равна 180°.
Слайд 74
Модуль «ГЕОМЕТРИЯ» №13 (4)
Повторение(2)
Ответ: 1.
Укажите номера верных утверждений
1.Через
любые две различные точки плоскости можно провести не более
одной прямой.2.Через любые две различные точки плоскости можно провести не менее одной прямой.
3.Если угол равен 54⁰, то вертикальный с ним угол равен 36⁰.
да
нет
да
нет
да
нет
Слайд 75
Повторение (подсказка)
Сформулируйте аксиому о взаимном расположении прямой и
точек на плоскости.
Сформулируйте свойство вертикальных углов
Вертикальные углы равны.
Через любые
две точки проходит прямая, и притом только одна.
Слайд 76
Модуль «ГЕОМЕТРИЯ» №13 (5)
Повторение(2)
Ответ: 13.
Укажите номера верных утверждений
1.Через
любую точку плоскости можно провести прямую.
2.Через любую точку плоскости
можно провести единственную прямую.3.Существует точка плоскости, через которую можно провести прямую.
да
нет
да
нет
да
нет
Слайд 77
Повторение (подсказка)
Сколько прямых можно провести через точку на
плоскости?
Через точку на плоскости можно провести бесконечно много прямых.
Существует
ли точка плоскости, через которую нельзя провести прямую?Через любую точку плоскости можно провести прямую.
Слайд 78
Модуль «ГЕОМЕТРИЯ» №13 (6)
Повторение(2)
Ответ: 1.
Укажите номера верных утверждений
1.Если
две параллельные прямые пересечены третьей прямой, то соответственные углы
равны.2.Если две параллельные прямые пересечены третьей прямой, то сумма внутренних односторонних углов равна 90⁰
3.Если при пересечении двух прямых третьей соответственные углы равны, то прямые перпендикулярны.
да
нет
да
нет
да
нет
Слайд 79
Повторение (подсказка)
Сформулируйте свойство параллельных прямых относительно соответственных углов
Если
две параллельные прямые пересечены третьей прямой, то соответственные углы
равныСформулируйте свойство параллельных прямых относительно внутренних односторонних углов.
Если две параллельные прямые пересечены третьей прямой, то сума внутренних односторонних углов равна 180°
Слайд 80
Модуль «ГЕОМЕТРИЯ» №13 (7)
Повторение(3)
Ответ: 3.
Укажите номера верных утверждений
1.Если
при пересечении двух прямых третьей сумма внутренних накрест лежащих
углов равна 180⁰, то прямые параллельны2.Если при пересечении двух прямых третьей соответственные углы равны 75⁰ и 105⁰, то прямые параллельны
3.Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180⁰, то прямые параллельны
да
нет
да
нет
да
нет
Слайд 81
Повторение (подсказка)
Сформулируйте признак параллельности двух прямых относительно накрест
лежащих углов.
Сформулируйте признак параллельности двух прямых относительно соответственных углов.
Сформулируйте
признак параллельности двух прямых относительно внутренних односторонних углов.Если при пересечении двух прямых третьей накрест лежащие углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей соответственные углы равны, то прямые параллельны.
Если при пересечении двух прямых третьей сумма внутренних односторонних углов равна 180°, то прямые параллельны.
Слайд 82
Рекомендации учителю
1. В работе по математике и при
подготовке к экзамену опираться на требования нового образовательного стандарта
и примерных программ к нему; составить планирование с учетом кодификаторов экзаменационных заданий (с 7 класса);2. Тренировать учащихся, постепенно увеличивая объём и сложность заданий, постепенно увеличивая скорость их выполнения, направляя их на поиск оптимальных путей решения математических задач;
Слайд 83
3. Использовать при подготовке учащихся к ГИА новые
формы и методы работы с дидактическим материалом; тренинги, репетиционные
экзамены, деловые игры и т.д.Рекомендации учителю
4. Активнее вводить тестовые технологии в систему обучения. Тренировочные тесты проводить по каждой теме с жестким ограничением времени.
Слайд 84 5. Математика в школе должна быть красивой, должна
быть интересной и полезной сейчас, а не в каком-то
отдаленном будущем, уроки должны нравиться ученикам – тогда и их отношение к ГИА по математике будет позитивным, а результаты – положительными.Рекомендации учителю
6. Набивание руки или как говорят «натаскивание» школьника на ГИА необходимо, однако, как показывает опыт, работу нельзя сводить только к этому. Этот этап проводится в конце, после того, как заложен фундамент.
Слайд 85
Рекомендации ученикам:
1. Объективно оцените
свой актуальный уровень знаний, пройдя тестирование по результатам обучения
в 8-ом классе.2. Качественно подготовьте школьный материал, создайте багаж фундаментальных знаний. Необходимо знать основные теоремы и формулы, алгоритмы выполнения заданий.
3. Пройдите организационный инструктаж (правила поведения на экзамене, правила заполнения бланков). Познакомьтесь со структурой и содержанием экзаменационной работы.
Слайд 86 4. Научитесь выделять и понимать главное в материале,
т.к. умение решать задачи является следствием глубоко понятого соответствующего
теоретического материала.5. Совершенствуйте свои вычислительные умения и навыки.
Рекомендации ученикам
Слайд 87
Модуль «Геометрия» содержит 8 заданий: в части 1
- 5 заданий, в час-
ти 2 - 3 задания.
Книги
по подготовке к ГИА
Слайд 88
Модуль «Геометрия» содержит 8 заданий: в части 1
- 5 заданий, в час-
ти 2 - 3 задания.
1.
ОТКРЫТЫЙ БАНК ЗАДАНИЙ ПО МАТЕМАТИКЕhttp://mathgia.ru/or/gia12/ShowProblems.html?posMask=8192&showProto=true
2. ПОДГОТОВКА К ГИА ПО МАТЕМАТИКЕ, КНИГИ МОЖНО СКАЧАТЬ
http://4ege.ru/gia-matematika/
3. ОНЛАЙН-ТЕСТЫ ПО НОВОЙ ФОРМЕ – 2013г. (1 вариант)
http://5ballov.qip.ru/test/gia/
4. ОНЛАЙН-ТЕСТЫ 2013г. , 2014г.
http://uztest.ru/exam?idexam=28
5. Видео разбор демоверсии ГИА 2013 по математике
http://4ege.ru/gia-matematika/2715-video-razbor-demoversii-gia-2013-po-matematike.html
6. ОНЛАЙН-ТЕСТЫ ПО НОВОМУ ПЛАНУ ГИА в 9 вариантах
http://ege.yandex.ru/mathematics-gia/
7. Тренировочные тесты для подготовки к ГИА (2013). (Личный сайт учителя Фоновой Натальи Леонидовны)
http://madam-fonova.ucoz.ru/publ/testy_dlja_podgotovki_k_gia_po_matematike_9_klass/30-1-2
8. ОНЛАЙН - тесты – 2013г.
http://free-math.ru/load/gia_po_matematike/online_testy/47
9. Переводной экзамен для учащихся 8 класса по математике (Бессонова Ж.П.)
http://easyen.ru/load/math/8_klass/perevodnoj_ehkzamen_dlja_uchashhikhsja_8_klassov/39-1-0-4193