Слайд 2
ПОВТОРЕНИЕ:
1 ВОПРОС:
Назовите признаки делимости на 2.
Ответ: Если последняя
цифра числа четная, то число делится на 2
Примеры:
222,
348, 27844338. 1111111112, 333333330, 7777799933555116 –
данные числа делятся на 2;
222, 348, 27844338. 1111111112, 333333330, 7777799933555116
Слайд 3
2222223, 864243, 1000005, 668884442229 –
не делятся
на 2.
2222223, 864243, 1000005, 668884442229
Сколько четных цифр вы знаете?
Назовите.
Правильный ответ.
Существует 5 четных цифр: 0, 2,4,6,8.
Слайд 4
2 ВОПРОС:
Назовите признаки делимости на 5.
Ответ: Если последняя
цифра числа 5 или 0, то число делится на
5.
Делятся ли данные числа на 5?
375
75
15
100
20
123
Примеры: 375 : 5 = 75; 75 : 5 = 15; 15 : 5 = 3.
100 : 5 = 20; 20 : 5 = 4
123 : 5 = 24 + остаток 3
Слайд 5
3 ВОПРОС:
Назовите признаки делимости на 10.
Ответ: Если
число оканчивается цифрой 0, то число делится на 10
целиком.
Делятся ли числа 100, 23840, 200005 на 10 без остатка?
Примеры: 100 : 10 = 10; 23840 : 10 = 2384
105 : 10 = 10 + остаток 5
Слайд 6
4 ВОПРОС:
Сформулируйте признак делимости на 25.
Ответ: Если число,
образованное двумя последними цифрами заданного числа, делится на 25,
то и все заданное число делится на 25 .
Если число заканчивается на 25, 50, 75, 00, то все число делится на 25 без остатка.
Примеры: 375 : 25 = 15; 550 : 25 = 22; 775 : 25 = 31; 1000000 : 25 = 40000
10005 : 25 = 400 + остаток 5
Слайд 7
5 ВОПРОС:
Сформулируйте признаки делимости на 4.
Ответ:
Если число, образованное двумя последними цифрами заданного числа, делится
на 4, то и все заданное число делится на 4.
Примеры: 416 : 4 = 104, 928 : 4 = 232
417 : 4 = 104 + остаток 1
Слайд 8
Практическое задание № 1.
На координатной оси отметьте точки,
выполняя следующие условия:
1 ЭТАП: для построения первой фигуры соедините
между собой точки, координаты которых делятся на 2 без остатка:
А (4;8); В(2;8); С (7;4); D(2;2); Е (3; 5); F (4;2).
2 ЭТАП: для построения второй фигуры соедините между собой точки, координаты которых состоят только из четных чисел:
А (8;8); В(8;6); С (7;1); D(6;2); Е (3; 5); F (8;2).
Слайд 9
3 ЭТАП: для построения третьей фигуры соедините между
собой точки, координаты которых можно определить, выполнив действие сокращения
дробей:
А (50/5;200/25); В(250/25;100/25); С (48/4;4/2); D(300/25;80/10); Е (120/10; 50/25).
ПРОВЕРЬТЕ СЕБЯ:
А (10;8), В (10;4), С (12;4), D (12;8), Е(12;2).
4 ЭТАП: подумайте и постройте недостающий фрагмент, записав самостоятельно координаты контрольных точек.
ПРОВЕРЬТЕ СЕБЯ:
А (14;8), В (14;2), С (16;8), D (16;2).
Слайд 11
Зимние Олимпийские игры 2014 (англ. 2014 Winter Olympics,
фр.официальное название XXII зимние Олимпийские игры) — международное спортивное
мероприятие, которое проходило в российском городе Сочи с 7 по 23 февраля 2014 года. Столица Олимпийских игр Сочи 2014 была выбрана во время 119-й сессии МОК в городе Гватемала, столице Гватемалы 4 июля 2007 года. На территории России Олимпийские игры проходили во второй раз (до этого в Москве в 1980 году прошли XXII летние Олимпийские игры), и впервые — зимние Игры. По окончании Олимпийских игр на тех же объектах будут проведены зимние Паралимпийские игры 2014. Организацией зимних Олимпийских и Паралимпийских игр 2014 занимается Оргкомитет «Сочи 2014».
Слайд 12
«Обучение математике – это в первую очередь решение
задач.
Задачи выступают как главное средство индивидуализации обучения математике.
Развитие мышления и способности к математической деятельности осуществляется в ходе самостоятельных размышлений учащихся над задачами.
Умение решать задачи – критерий успешности обучения математике. Самостоятельная деятельность учащихся по решению задач занимает главное место в обучении математике» («Концепция математического образования», глава 3 «Общие принципы», пункт 5).
Слайд 13
Практическое ЗАДАНИЕ № 2
В ходе подготовки к
XXII Зимним олимпийским играм было построено множество спортивных объектов
самого различного направления. В один из дней в гостиничный комплекс было зарегистрировано для проживания 159 спортсменов. Подумайте логически, т.е. не производя вычислений, и ответьте на вопрос:
Можно ли разместить спортсменов в количестве 159 человек на трех этажах гостиничного комплекса равномерно, т.е. поровну на каждом этаже?
Слайд 14
159 = 100 + 50 + 9
100 :
3 = 33 + остаток 1
50 : 3 =
16 + остаток 2
9 + 1 + 2 = 12 человек
12 : 3 = 4
Вывод: Можно 159 человек расположить поровну н трех этажах гостиничного корпуса.
Проверка: 159 : 3 = 53 (без остатка).
Слайд 15
Практическое задание № 3
Используя вышеуказанный прием, ответьте
на следующий вопрос:
В церемонии закрытия XXII Зимней Олимпиады для
организации посадочных мест на трибунах были задействованы 189 волонтеров. Можно ли такое количество волонтеров расположить в 9 секторах равномерно?
Слайд 16
189 = 100 + 80 + 9
100 :
9 = 11 + ОСТАТОК 1
80 : 9 =
8 + ОСАТТОК 8
1 + 8 + 9 = 18
18 : 9 = 2 ( ОСТАТОК 0)
Обратите внимание на остатки:
1, 8 и последняя цифра 9 целиком совпадают с записью рассматриваемого числа.
Выполняя последнее действие, мы получили сложение цифр, с помощью которых было записано число:
1 + 8 + 9 = 18
Слайд 17
1 + 8 + 9 = 18
18 :
9 = 2 (без остатка)
Постарайтесь сформулировать признак делимости на
9, используя выводы решения задачи.
Проверьте правильность сделанных выводов на числах:
577
577 : 9 = 64,1
693
693 : 9 = 77
Слайд 18
Проверьте правильность своих выводов и наблюдения по задаче
ПРАКТИЧЕСКОГО ЗАДАНИЯ № 2:
159 : 3 = 53
1 +
5 + 9 = 15
15 : 3 = 5 (остаток 0)
Убедитесь еще раз, проверив делимость на 3 следующих чисел:
465
465 : 3 = 155
565
565 : 3 = 188 (остаток 1)
Слайд 19
ПРИЗНАКИ ДЕЛИМОСТИ НА 3 и 9:
Признак делимости на
3:
Натуральное число делится на 3 тогда и только тогда,
когда делится на 3 сумма его цифр.
Признак делимости на 9:
Натуральное число делится на 9 тогда и только тогда, когда делится на 9 сумма его цифр.
Слайд 20
Практическое задание № 4
(выполнятся в группах)
Выберите номер правильного
ответа:
I вопрос: Какое из чисел делится на 3 без
остатка?
1. 6688
2. 35489
3. 1637
4. 456378
Если Вы считаете, что правильный ответ отсутствует, запишите 0.
Слайд 21
II вопрос: Какое из чисел делится на 9
без остатка?
1. 6687
2. 35489
3. 1637
4. 456378
Если Вы считаете, что
правильный ответ отсутствует, запишите 0.
Слайд 22
III вопрос:
Любое число, если оно делится на
3, то оно делится на 9.
1. Любое
2. Только четное
3.
Только нечетное
Если Вы считаете, что правильный ответ отсутствует, запишите 0.
Слайд 23
IV вопрос:
Любое число, если оно делится на
9, то оно делится на 3.
1. Только нечетное
2. Любое
3.
Только четное
Если Вы считаете, что правильный ответ отсутствует, запишите 0.
Ответ обоснуйте, приведя примеры.
Слайд 25
Практическое задание № 5
Определите, какие значения можно поставить
в вместо *, чтобы выполнялось деление на 3 без
остатка:
2*8
2, т.к. 2 + 2+ 8 = 12
5, т.к. 2 + 5 + 8 = 15
8, т.к. 2 + 8 + 8 =18
Слайд 26
Определите, какие значения можно поставить в вместо *,
чтобы выполнялось деление на 9 без остатка:
37*4
3 + 7
+ 4 = 14
4, т.к. 3 + 7+ 4 + 4 = 18
*678
6, т.к. 6 + 6+ 7 + 8 = 27
Слайд 32
А у нас с Вами будет свой
пьедестал
почета!!!
Практическое задание № 6.
Для его выполнения необходимо правильно
рассчитать свои силы и выбрать уровень сложности задания:
- золотой;
- серебряный;
- бронзовый.
Но не следует забывать и про известную поговорку:
«РИСК – БЛАГОРОДНОЕ ДЕЛО!!!»
Слайд 33
Задание 1.
Выберите числа, которые делятся без остатка на
3:
Золотой уровень Серебряный уровень
Бронзовый уровень
1. 85749604 1. 75845 1. 878
2. 85746389 2. 8590 2. 859
3. 95847589 3. 859 3. 99
Слайд 34
Задание 2.
Выберите числа, которые делятся без остатка на
9:
Золотой уровень Серебряный уровень
Бронзовый уровень
1. 85749604 1. 75845 1. 878
2. 85746389 2. 8590 2. 859
3. 95847589 3. 859 3. 99
Слайд 35
Задание 3:
Вставьте недостающие цифры, чтобы число делилось на
3 без остатка:
Золотой уровень
Серебряный уровень Бронзовый уровень
1. 85*775 1. 75*4 1. 8*4
2. 88*111 2. 8*45 2. 3*5
Слайд 36
Задание 4:
Вставьте недостающие цифры, чтобы число делилось на
9 без остатка:
Золотой уровень
Серебряный уровень Бронзовый уровень
1. 85*775 1. 75*4 1. 8*4
2. 88*111 2. 8*45 2. 3*5
Слайд 37
Задание 4:
Сократите дроби:
Золотой уровень
Серебряный уровень Бронзовый уровень
109755 1083 819
62046 1593 981
Слайд 38
Задание 5:
составьте из единиц как можно больше вариантов
чисел так, чтобы они делились без остатка на 3
и 9 .
Слайд 39
Молодцы!
Пусть ваши результаты будут только на золотую медаль!
Слайд 42
Практическое задание № 6:
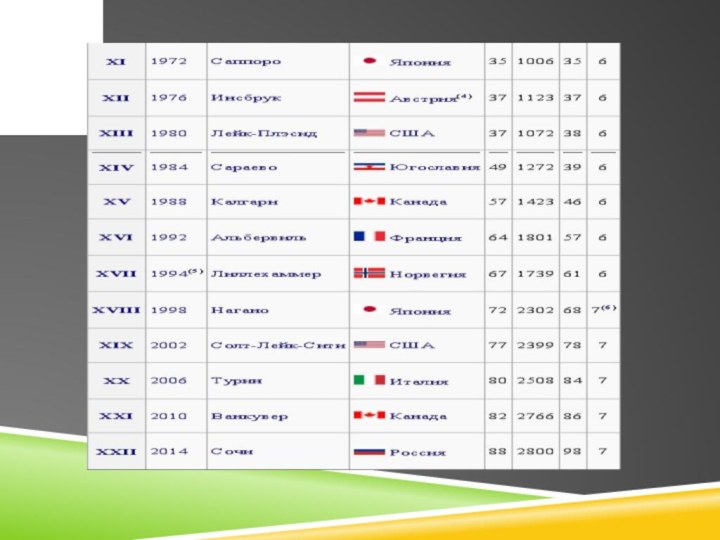
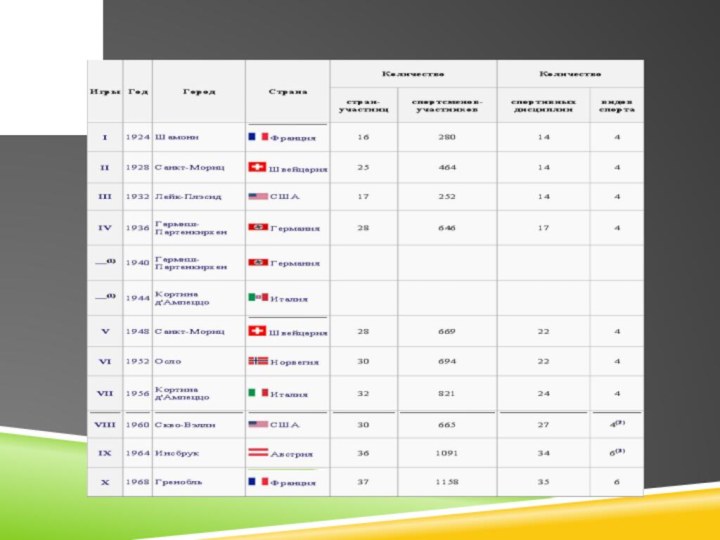
Условие. Известно, что в I

и II зимних Олимпийских играх число стран – участниц
оставалось неизменным. В дальнейшем олимпийское движение прогрессировало, и все большее и большее количество стран стали принимать участие в спортивных соревнованиях самого престижного уровня. Определите, сколько стран – участниц было:
на III зимней Олимпиаде, если количество участников уменьшилось на 2;
на VII зимней Олимпиаде, если количество стран увеличилось на 10 по сравнению с первой Олимпиадой;
на IX, если количество увеличилось на 10 относительно VII зимних Олимпийских игр;
сколько стран – участниц было на XVIII Олимпиаде, если их количество удвоилось по сравнению с IX зимними Олимпийскими играми;
также, сколько стран принимали участие в Сочи – 2014, если известно, что их количество увеличилось на 30 по сравнению с XVIII Олимпийскими играми? Необходимо учесть, что в перечисленных выше зимних олимпийских играх приняли в общей сложности 264 страны.
Примечание. Можно составлять самые разнообразные задачи по данному принципу, используя различные комбинации данных Приложения 1, что может быть использовано на уроках математики в рамках темы «Решение задач с помощью составления уравнений».
Слайд 43
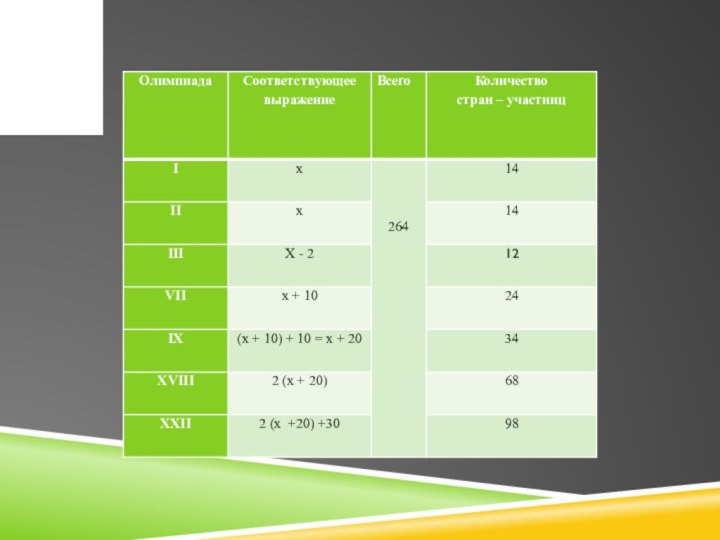
Чтобы ускорить решение задачи, заполните следующую таблицу:
Слайд 44
Проверьте правильность заполнения:
Слайд 45
Составьте и решите уравнение.
Проверьте правильность уравнения:
х + х
+(х – 2 )+ (х +10) +(х+20)+2(х +20) +2(х
+20) + 30 = 264
4х + 8 + х + 20 + 2х +40 +2х +40 +30 =264
9х +138 = 264
9х = 264 – 138
9х = 126
х = 126 : 9
х = 14.
Зная, что Х – количество участников на I зимней олимпиаде, найдите количество остальных стран – участниц.
Проверьте:
Слайд 47
В заключении отмечу еще раз тезис «Концепции математического
образования»:
«Опыт, приобретаемый в процессе решения математических задач, способствует
развитию как навыков рационального мышления, так и интуиции – способности предвидеть результат и предугадать путь решения. Математика пробуждает воображение».