- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Векторы.Координаты вектора
Содержание
- 3. Вектор характеризуется следующими элементами: 1) начальной точкой
- 4. Абсолютной величиной (или модулем) вектора называется длина
- 5. На рисунках вектор изображается отрезком со стрелкойАВАВВектор АВ, А – начало вектора, В – конец.DCEFKL
- 6. Векторы часто обозначают и одной строчной
- 7. Длиной или модулем ненулевого вектора АВ называется
- 8. Коллинеарные векторыНенулевые векторы называются коллинеарными, если они
- 9. аbcdmnsL
- 10. Нулевой вектор считается коллинеарным любому вектору, так как он сонаправлен с любым вектором.a 0a•P
- 11. Равенство векторов 1 Определение.
- 13. Противоположные векторы Пусть
- 14. Вектор, противоположный вектору c, обозначается так: -c.c- cОчевидно, с+(-с)=0 или АВ+ВА=0
- 15. Сумма двух векторов Законы сложения векторов: I. a
- 16. Рассмотрим пример: Петя из
- 17. Координаты вектора в пространстве
- 18. Единичный вектор – вектор, длина которого равна
- 19. Любой вектор ā можно разложить по координатным
- 20. Запись координат вектора.Координаты вектора а будут записываться
- 21. Правила нахождения суммы, разности и произведения на
- 22. Разность векторов: Каждая координата разности двух векторов
- 23. Произведение вектора на число: Каждая координата
- 24. Произведение вектора на число: Каждая координата
- 25. Сложение векторовПравило треугольника.Правило параллелограмма.Правило многоугольника.Правило параллелепипеда.
- 26. Правило
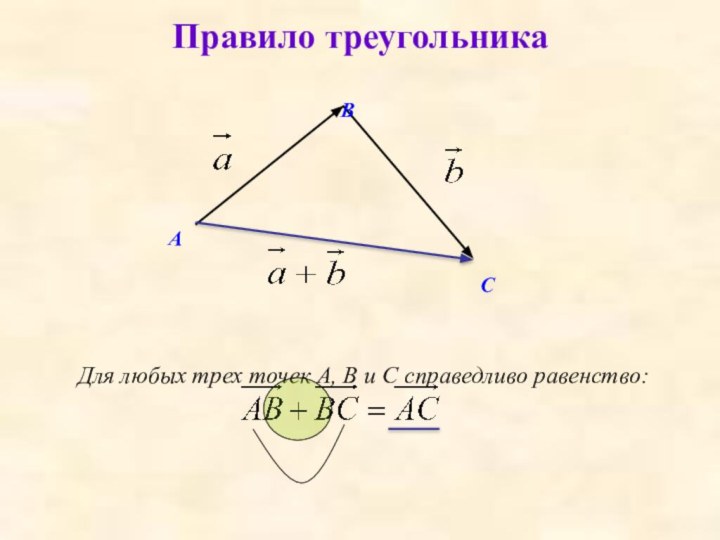
- 27. Правило треугольникаАBCДля любых трех точек А, В и С справедливо равенство:
- 28. Правило параллелограмма
- 29. Сумма нескольких векторов
- 30. Правило параллелепипеда: вектор, образующий диагональ параллелепипеда, равен
- 31. Вычитание векторов Определение.
- 32. Умножение вектора на число
- 33. Произведением нулевого вектора на
- 34. Умножение вектора на число Для
- 35. Свойства действий над векторами позволяют в выражениях,
- 36. Компланарные векторы [от лат. com (cum) —
- 37. Векторы CA, CA1 и DD1 -компланарны, так
- 38. Признак компланарности трех векторовЕсли вектор с можно
- 39. Разложение вектора по координатным векторам
- 40. Векторы называются коллинеарными, если они параллельны.Если векторы
- 41. Связь между координатами векторов и координатами точек
- 42. Вектор, конец которого совпадает с данной точкой,
- 43. Простейшие задачи в координатах
- 44. 1. Координаты середины отрезка.ОАВСDхуzA (x1; y1; z1),
- 45. Угол между векторами
- 46. ОАВα Если а || b и а
- 47. Скалярное произведение векторов
- 48. Скалярное произведениеСкалярным произведением двух векторов называется произведение их длин на косинус угла между ними.
- 49. a · b = | a
- 50. Скачать презентацию
- 51. Похожие презентации
Определение. Отрезок, для которого указано, какой из его концов считается началом, а какой - концом, называется направленным отрезком или вектором.






























![Презентация по математике на тему Векторы.Координаты вектора Компланарные векторы [от лат. com (cum) — совместно и planum — плоскость],](/img/tmb/6/505881/8a36868d2cd73f2ba8eff947d40f7420-720x.jpg)











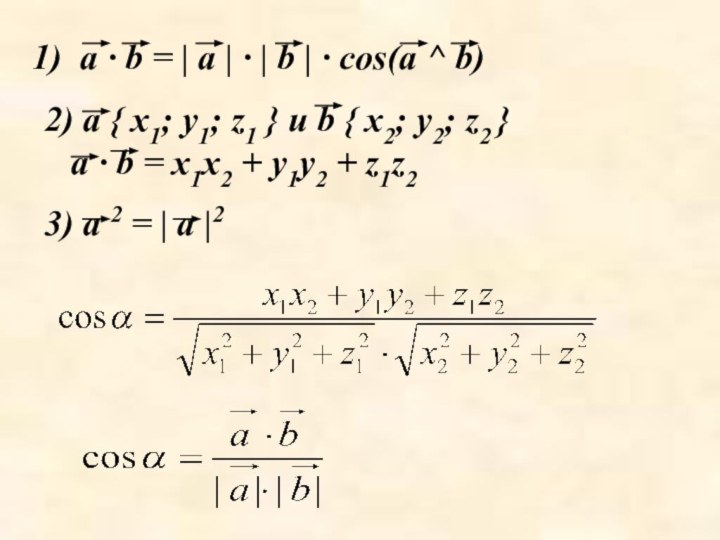

Слайд 3
Вектор характеризуется следующими элементами:
1) начальной точкой (точкой
приложения);
2) направлением;
3) длиной («модулем вектора»).
Слайд 4 Абсолютной величиной (или модулем) вектора называется длина отрезка,
изображающего вектор. Абсолютная величина вектора a .
Обозначается a .
a
•
•
B
A
•
•
•
B
A
a
Слайд 5
На рисунках вектор изображается отрезком со стрелкой
АВ
А
В
Вектор АВ,
А – начало вектора, В – конец.
D
C
E
F
K
L
Слайд 6 Векторы часто обозначают и одной строчной латинской
буквой со стрелкой над ней:
b
Любая точка плоскости также является
вектором, который называется НУЛЕВЫМ. Начало нулевого вектора совпадает с его концом: c
a
М
ММ
=
0
Слайд 7 Длиной или модулем ненулевого вектора АВ называется длина
отрезка АВ:
АВ = а = АВ =
5с
a
В
А
с = 17
Длина нулевого вектора считается равной нулю:
ММ = 0.
М
Слайд 8
Коллинеарные векторы
Ненулевые векторы называются коллинеарными, если они лежат
либо на одной прямой, либо на параллельных прямых. Допусти́м,
но не рекомендуется, синоним «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены («сонаправлены») или противоположно направлены (в последнем случае их иногда называют «антиколлинеарными» или «антипараллельными»).Слайд 10 Нулевой вектор считается коллинеарным любому вектору, так как
он сонаправлен с любым вектором.
a 0
a
•
P
Слайд 11
Равенство векторов
1 Определение.
Векторы
называются равными, если они сонаправлены и их длины равны.
а = b , еслиа b
а = b
а
c
b
d
n
f
m
s
Слайд 12
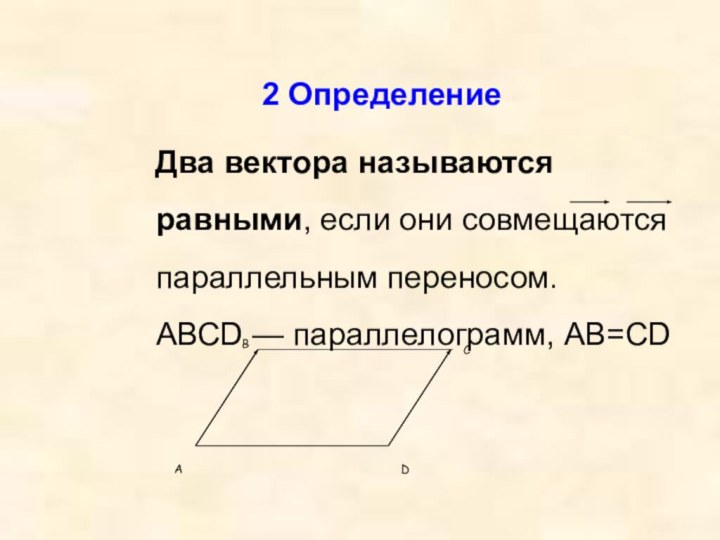
2 Определение
Два вектора называются равными, если они
совмещаются параллельным переносом.
АВСD — параллелограмм, AB=CDB
C
A
D
Слайд 13
Противоположные векторы
Пусть а
– произвольный ненулевой вектор.
Определение. Вектор b
называется противоположным вектору а, если а и b имеют равные длины и противоположно направлены.a = АВ, b = BA
a
B
А
b
Слайд 15
Сумма двух векторов
Законы сложения векторов:
I. a +
b = b + a
( П е р
е м е с т и т е л ь н ы й закон ).II. ( a + b ) + c = a + ( b + c )
( С о ч е т а т е л ь н ы й закон ).
III. a + 0 = a .
IV. a + (– a ) = 0 .
Слайд 16
Рассмотрим пример:
Петя из дома(D)
зашел к Васе(B), а потом поехал в кинотеатр(К).
В результате этих двух перемещений, которые можно представить векторами DB и BK, Петя переместился из точки D в К, т.е. на вектор DК:
DK=DB+BK.
Вектор DK называется суммой векторов DB и BK.
D
B
K
Слайд 18
Единичный вектор – вектор, длина которого равна 1.
i
– единичный вектор оси абсцисс, j – единичный вектор
оси ординат, k – единичный вектор оси аппликат.x
z
y
O
Слайд 19 Любой вектор ā можно разложить по координатным векторам,
т.е. представить в виде:
Нулевой вектор можно представить в виде:
Координаты
равных векторов соответственно равны, т.е., если ā { x1; y1; z1 } = b { x2; y2; z2 }, то
x1 = x2, y1 = y2, z1 = z2.
Слайд 20
Запись координат вектора.
Координаты вектора а будут записываться в
фигурных скобках после обозначения вектора: а {x; y; z}.
На рисунке справа изображен прямоугольный параллелепипед имеющий измерения: OA =2, OA =2, OA =3.
Координаты векторов изображенных на этом рисунке, таковы:
a {2; 2; 4}, b {2; 2; -1},
A A {2; 2;0}, i {1; 0; 0},
j {0;1;0}, k {0; 0; 1}
A
A
A
A
O
y
x
z
a
j
i
k
b
3
2
1
1
2
3
3
Слайд 21 Правила нахождения суммы, разности и произведения на данное
число.
Сумма векторов:
Каждая координата суммы двух или более векторов
равна сумме соответствующих координат этих векторов. Если a {x1;y1;z1} и b {x2;y2;z2} – данные векторы, то вектор a + b имеет координаты
a + b = { x1+ x2; y1+ y2; z1+ z2 }.
Слайд 22
Разность векторов:
Каждая координата разности двух векторов равна
разности соответствующих координат этих векторов.
Если a {x1;y1;z1} и
b {x2;y2;z2} – данные векторы, то вектор a – b имеет координаты
a – b = { x1 – x2; y1 – y2; z1 – z2 }.
Слайд 23 Произведение вектора на число: Каждая координата произведения вектора
на число равна произведение соответствующей координаты вектора на это
число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты αа = { αx; αy; αz }.Слайд 24 Произведение вектора на число: Каждая координата произведения вектора
на число равна произведение соответствующей координаты вектора на это
число. Если a {x; y; z } – данный вектор, α - данное число, то вектор αa имеет координаты αа = { αx; αy; αz }.
Слайд 25
Сложение векторов
Правило треугольника.
Правило параллелограмма.
Правило многоугольника.
Правило параллелепипеда.
Слайд 26
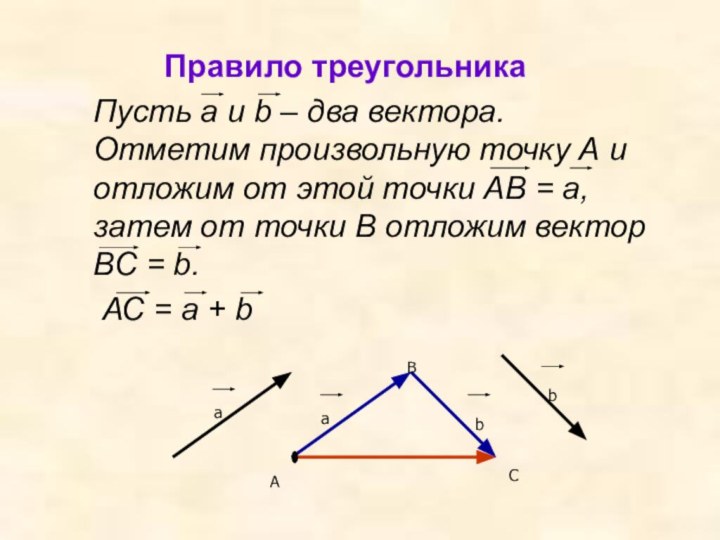
Правило треугольника
Пусть а и b – два вектора. Отметим
произвольную точку А и отложим от этой точки АВ = а, затем от точки В отложим вектор ВС = b.АС = а + b
a
a
b
b
B
A
C
Слайд 28
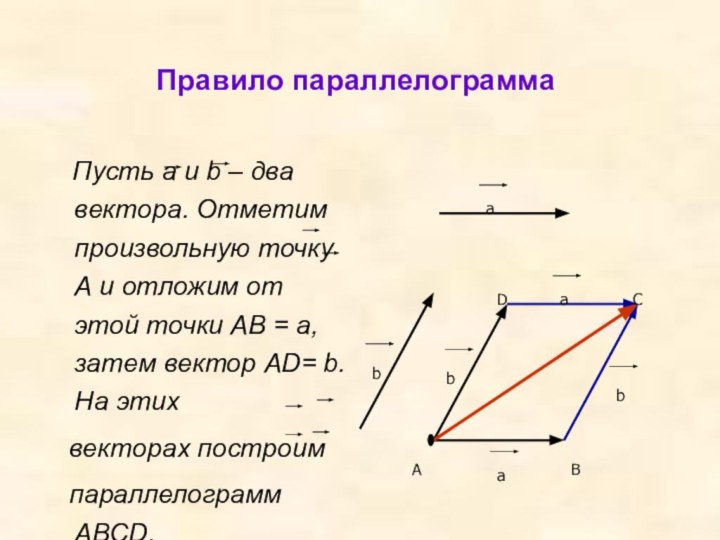
Правило параллелограмма
Пусть а и b
– два вектора. Отметим произвольную точку А и отложим от этой точки АВ = а, затем вектор АD= b. На этихвекторах построим
параллелограмм АВСD.
АС = АВ + BС = а+b
АС = АD + DС = b+a
a
a
a
b
b
b
D
C
A
B
Слайд 30 Правило параллелепипеда: вектор, образующий диагональ параллелепипеда, равен сумме
трёх векторов, исходящих из той же
вершины и образующих его рёбра. a + b + c = AM
Слайд 31
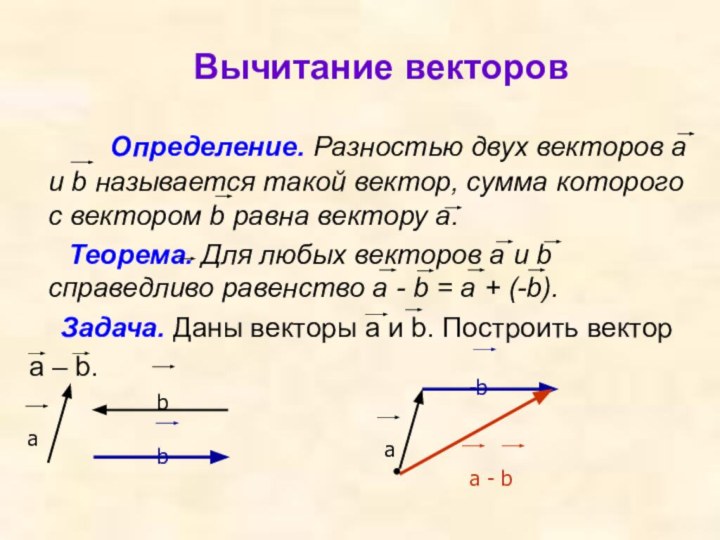
Вычитание векторов
Определение. Разностью
двух векторов а и b называется такой вектор, сумма
которого с вектором b равна вектору а.Теорема. Для любых векторов а и b справедливо равенство а - b = а + (-b).
Задача. Даны векторы а и b. Построить вектор
а – b.
а
b
-b
-b
а
a - b
Слайд 32
Умножение вектора на число
Определение. Произведением ненулевого
вектора а на число k называется такой вектор b, длина которого равна вектору k а , причем векторы а и b сонаправлены при k ≥ 0 и противоположно направлены при k < 0.а
3а
-2a
Слайд 33 Произведением нулевого вектора на любое
число считается нулевой вектор.
Для
любого числа k и любого вектора а векторы а и ka коллинеарны. Из этого определения следует также, произведение любого вектора на число нуль есть нулевой вектор.
Слайд 34
Умножение вектора на число
Для любых
чисел k, n и любых векторов а, b справедливы
равенства:1. (kn) а = k ( na ) (сочетательный закон)
2. (k + n) а = kа + na (первый распределительный закон)
3. k ( а + b ) = kа + kb (второй распределительный закон)
Слайд 35
Свойства действий над векторами позволяют в выражениях, содержащих
суммы, разности векторов и произведения векторов на числа, выполнять
преобразования по тем же правилам, что и в числовых выражениях. Например,p = 2( a – b) + ( c + a ) – 3( b – c + a ) =
= 2a – 2b + c + a – 3b + 3c – 3a = - 5b + 4c
Слайд 36
Компланарные векторы
[от лат. com (cum) — совместно
и planum — плоскость], векторы, параллельные одной плоскости.
Определение
Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.
Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.
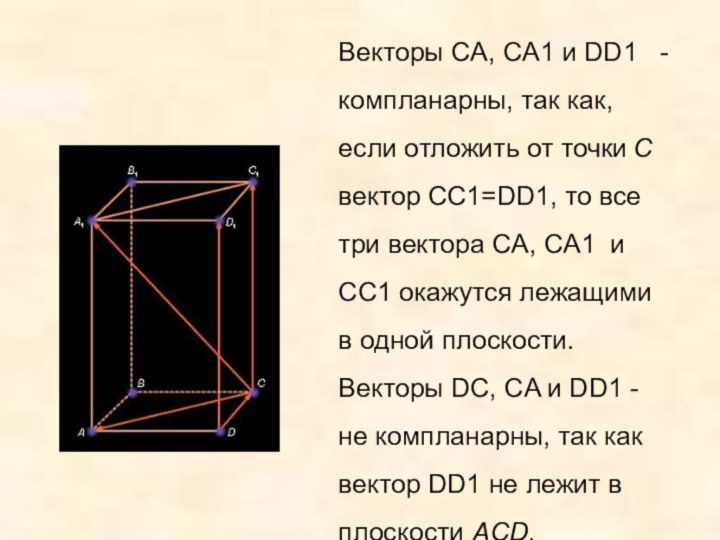
Слайд 37 Векторы CA, CA1 и DD1 -компланарны, так как,
если отложить от точки C вектор CC1=DD1, то все три
вектора CA, CA1 и CC1 окажутся лежащими в одной плоскости. Векторы DC, CA и DD1 - не компланарны, так как вектор DD1 не лежит в плоскости ACD.
Слайд 38
Признак компланарности трех векторов
Если вектор с можно разложить
по векторам a и b , т.е. представить в
видеc = x·a + y·b, где
где х и у — некоторые числа, то векторы a , b и c компланарны.
Слайд 40
Векторы называются коллинеарными, если они параллельны.
Если векторы а
{ x1; y1; z1 } и b { x2;
y2; z2 }, то:Слайд 42 Вектор, конец которого совпадает с данной точкой, а
начало – с началом координат, называется радиус-вектором данной точки.
Координаты
любой точки равны соответствующим координатам её радус-вектора.М (x; y; z)
OM (x; y; z)
A (x1; y1; z1), B (x2; y2; z2) AB (x2 – x1; y2 – y1; z2 – z1)
Слайд 44
1. Координаты середины отрезка.
О
А
В
С
D
х
у
z
A (x1; y1; z1), B
(x2; y2; z2), C (x; y; z)
– середина АВ.ОС = ½ (ОА + ОВ), тогда
2. Вычисление длины вектора по его координатам:
если а { x; y; z }, то
3. Расстояние между двумя точками:
Слайд 46
О
А
В
α
Если а || b и а и
b сонаправлены, то α = 0°.
Если a ||
b и a и b противоположно направлены, то α = 180°.Если а ⊥ b, то α = 90°.
Слайд 48
Скалярное произведение
Скалярным произведением двух векторов называется произведение их
длин на косинус угла между ними.
Слайд 49 a · b = | a |
· | b | · cos(a ^ b)
2) a
{ x1; y1; z1 } и b { x2; y2; z2 }
a · b = x1x2 + y1y2 + z1z23) a 2 = | a |2