всех трех условий.
У
О
Х
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему к уроку математики по теме: Криволинейная трапеция
Содержание
- 2. Является ли фигура 1 криволинейной трапецией? Проверьте
- 3. Нет, фигура 1 не является криволинейной трапецией,
- 4. Является ли фигура 2 криволинейной трапецией?У О
- 5. Да, фигура 2 удовлетворяет всем трем условиям:
- 6. Является ли фигура 3 криволинейной трапецией?3.У О
- 7. Нет, фигура 3 не является криволинейной трапецией,
- 8. Замечания: 1. Отрезки прямых, ограничивающих криволинейную трапецию
- 9. Какие из следующих шести фигур – криволинейные трапеции? Почему остальные фигуры не являются криволинейными трапециями?
- 10. У
- 11. Фигуры 1 и 2 удовлетворяют всем трем условиям и, следовательно, являются криволинейными трапециями.
- 12. У
- 13. Фигуры 3 и 4 – не криволинейные трапеции, так как они не ограничены осью абсцисс.
- 14. 5. У
- 15. Фигуры 5 и 6 - не криволинейные
- 16. Из каких криволинейных трапеций состоит следующая фигура?
- 17. Эта фигура состоит из криволинейных трапеций
- 18. Если обозначить площадь всей фигуры ММ1, NN1,
- 19. S = S1 + S2
- 20. Представьте площадь заштрихованной фигуры S как разность
- 21. У
- 22. 3. Представьте площадь заштрихованной фигуры S как
- 23. У
- 24. Криволинейной трапецией называется фигура, ограниченная:………………………….……………..
- 25. Скачать презентацию
- 26. Похожие презентации
Является ли фигура 1 криволинейной трапецией? Проверьте выполняемость всех трех условий.У О Х
Слайд 3 Нет, фигура 1 не является криволинейной трапецией, так
как она не ограничена осью абсцисс (не удовлетворяет первому
условию)Слайд 5 Да, фигура 2 удовлетворяет всем трем условиям: ограничена
осью абсцисс, двумя прямыми, параллельными оси ординат, и непрерывной
кривой, не пересекающей ось абсцисс; фигура 11 является криволинейной трапецией.Слайд 7 Нет, фигура 3 не является криволинейной трапецией, так
как она не ограничена справа (не удовлетворяет второму условию).
Слайд 8
Замечания:
1. Отрезки прямых, ограничивающих криволинейную трапецию слева
и справа, могут обратиться в точки.
2. Все линии, ограничивающие
криволинейную трапецию могут быть прямыми.Слайд 9 Какие из следующих шести фигур – криволинейные трапеции?
Почему остальные фигуры не являются криволинейными трапециями?
Слайд 11 Фигуры 1 и 2 удовлетворяют всем трем условиям
и, следовательно, являются криволинейными трапециями.
Слайд 15 Фигуры 5 и 6 - не криволинейные трапеции.
В фигуре 5 кривая не непрерывна. В фигуре 6
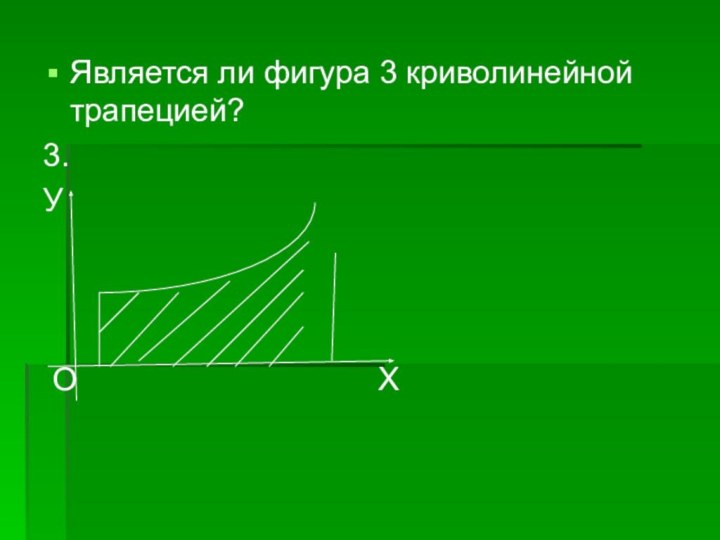
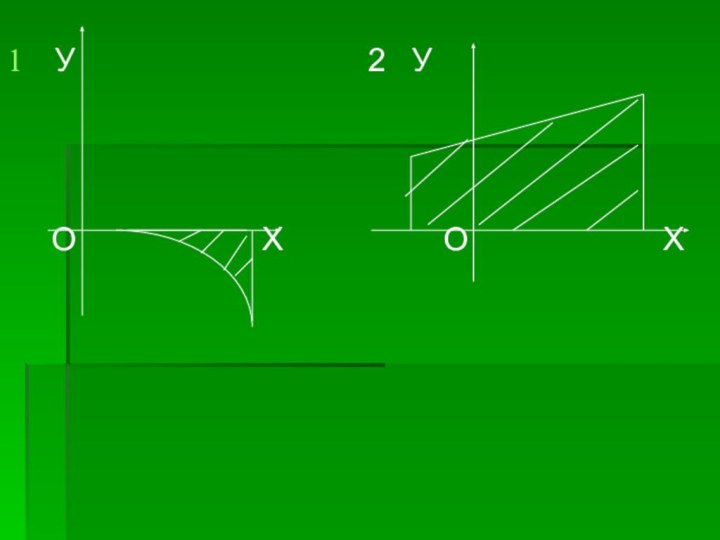
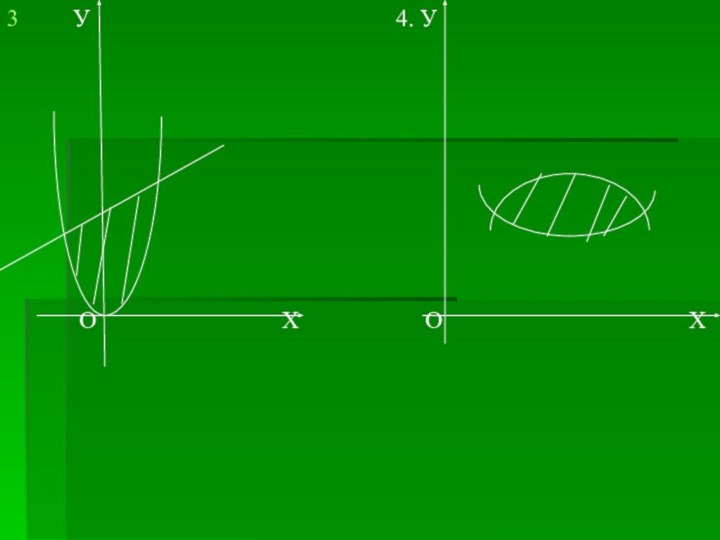
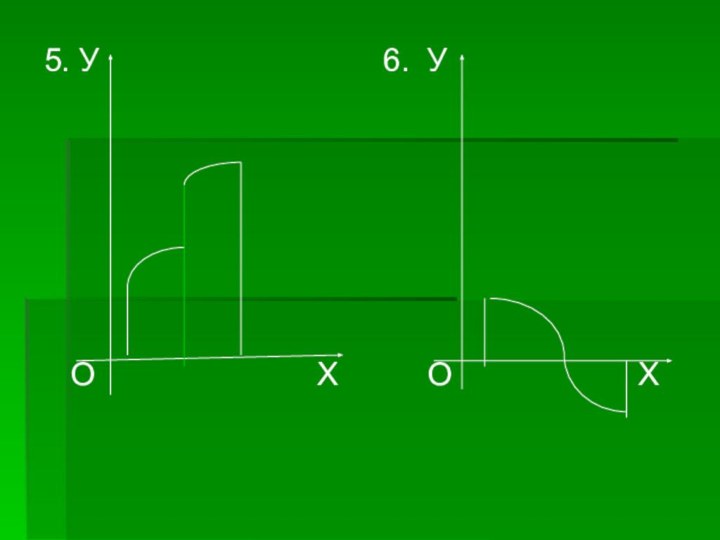
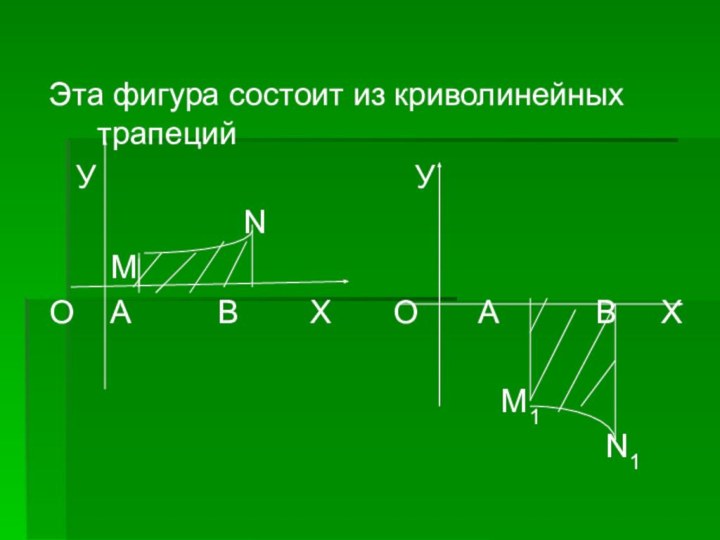
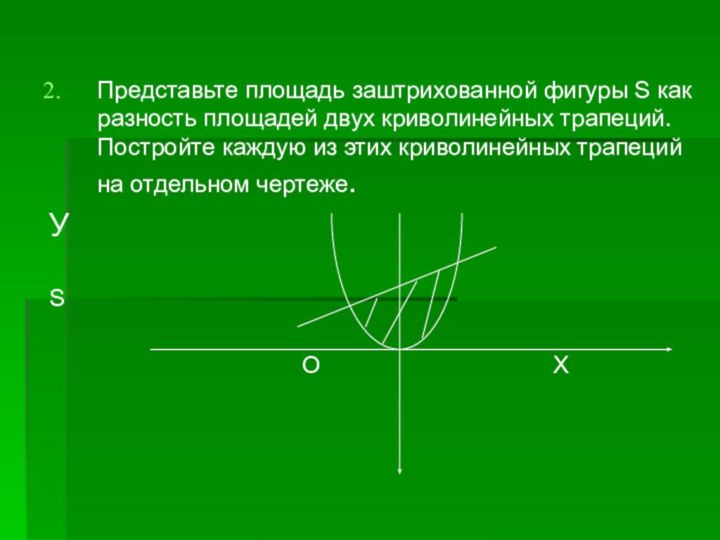
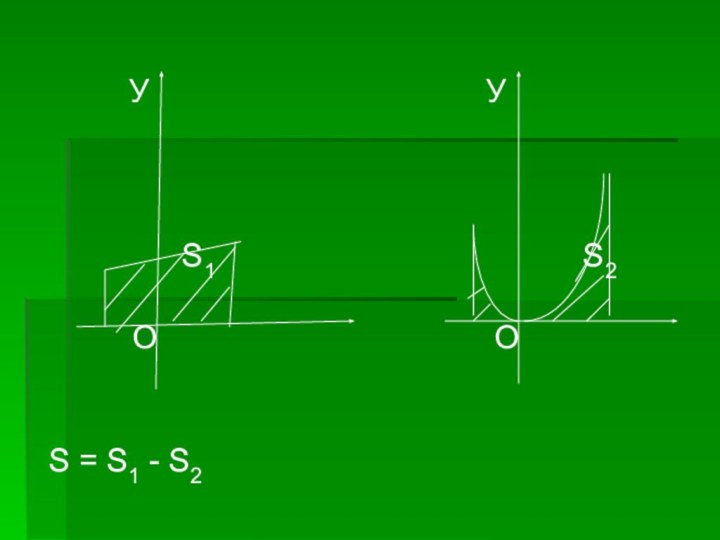
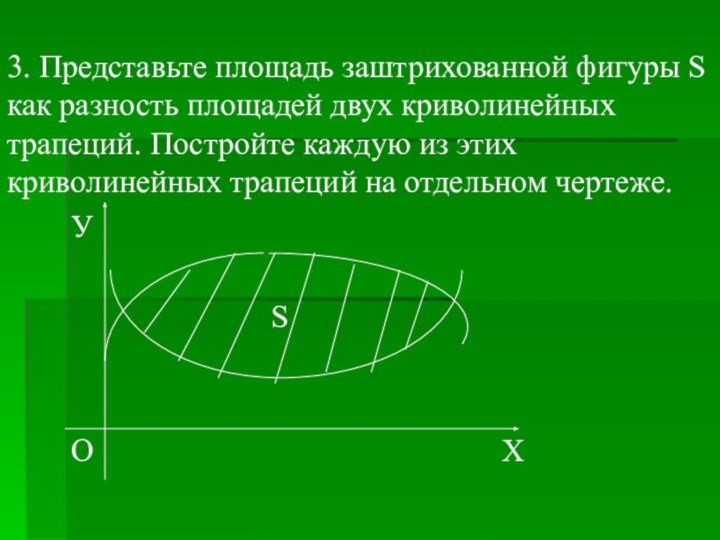
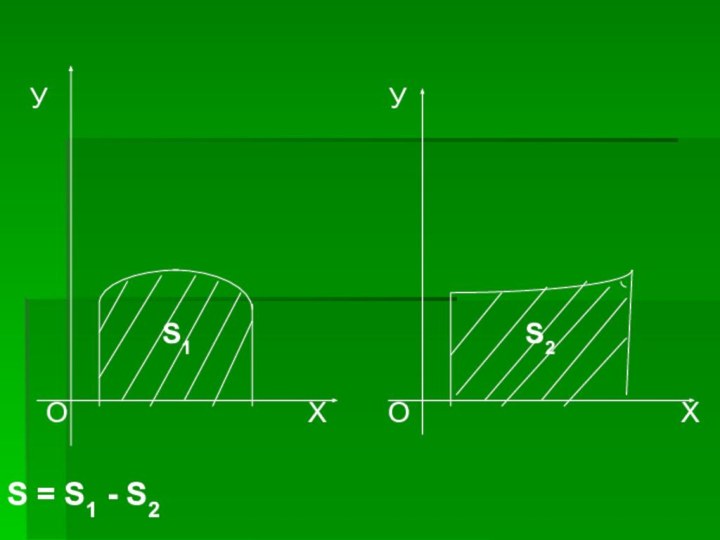
она пересекает ось абсциссПлощадь следующих ограниченных непрерывными линиями фигур, которые сами не являются криволинейными трапециями, можно представить как сумму или разность площадей криволинейных трапеций.
Слайд 16 Из каких криволинейных трапеций состоит следующая фигура? Постройте
каждую криволинейную трапецию на отдельном чертеже.
У
NM
О А В Х
M1
N1
Слайд 18 Если обозначить площадь всей фигуры ММ1, NN1, через
S, а площади криволинейных трапеций АМNB и AM1N1B через
S1 и S2 , то как выразить S через S1 и S2?Слайд 20 Представьте площадь заштрихованной фигуры S как разность площадей
двух криволинейных трапеций. Постройте каждую из этих криволинейных трапеций
на отдельном чертеже.У
S
O Х
Слайд 22 3. Представьте площадь заштрихованной фигуры S как разность
площадей двух криволинейных трапеций. Постройте каждую из этих криволинейных
трапеций на отдельном чертеже.У
S
О Х
