Слайд 3
Первая тропинка - о великом русском математике -
Николае Ивановиче Лобачевском
Лобачевский Николай Иванович –
великий математик,
творец неевклидовой геометрии.
(01.12.1792- 24.02.1856)
24.02.2015 года исполнилось 159 лет
со дня смерти великого математика –
Н.И. Лобачевского
Слайд 4
Н.И. Лобачевского сравнивают
с Колумбом, с Коперником,
называют
гением первого ранга. Знакомство с жизнью и деятельностью Николая
Ивановича раскрывает перед нами вдохновенный образ гениального ученого, неутомимого труженика.
В. Фирсов «Н.И. Лобачевский».
Высокий лоб, нахмуренные брови,
В холодной бронзе - отражённый луч…
Но даже неподвижный и суровый
Он, как живой, - спокоен и могуч.
Когда-то здесь, на площади широкой,
На этой вот казанской мостовой,
Задумчивый, неторопливый, строгий,
Он шёл на лекции- великий и живой.
Пусть новых линий не начертят руки,
Он здесь стоит, взнесённый высоко,
Как утверждение бессмертья своего,
Как вечный символ торжества науки.
Слайд 5
1 декабря 1792 года в Нижнем Новгороде родился
Николай Иванович Лобачевский - русский математик, творец неевклидовой геометрии.
Он родился в семье мелкого чиновника. Бедность и недостатки окружали колыбель мальчика.
С 14 лет жизнь Н.И. Лобачевского связана с Казанским университетом.
С 1814 года (в 22 года) Н.И. Лобачевский преподаёт в университете: читает лекции по математике, физике, астрономии, заведует обсерваторией, возглавляет библиотеку. В течение нескольких лет он избирался деканом физико-математического факультета.
С 1827 года начинается 19- летний период его непрерывного ректорства. Всё надо было начинать заново: заниматься строительством, привлекать новых профессоров, менять студенческий режим. На это уходило почти всё время.
Слайд 6
В начале февраля 1826 года Н.И. Лобачевский передал
в университет рукопись Сжатое изложение начал геометрии со строгим
доказательством теоремы параллельных. 11 февраля он выступил с докладом на заседании Совета университета. Но никто из присутствующих не мог уследить за ходом мысли Лобачевского. Созданная комиссия из членов Совета несколько лет не давала заключения.
В 1830 года В Казанском вестнике выходит работа О началах геометрии. Через 2 года, в 1832 года Статью послали в Петербург. И здесь никто ничего не понял, работа была квалифицирована как бессмысленная. Учёные мира ещё не были готовы воспринять идеи новой геометрии Н.И. Лобачевского.
Слайд 7
Ничто не могло поколебать уверенности Н.И. Лобачевского в
своей правоте. В течение 30 лет он продолжает развивать
свою геометрию. Но его идеи не получили признание. Гениальное открытие учёного было осмеяно, над ним издевались, его унижали и оскорбляли. Научный подвиг великого геометра не был оценён.
Преследования Лобачевского не прекратились и в последние годы его жизни. Полного сил, энергии и новых замыслов, Н.И. Лобачевского уволили на пенсию и отстранили от должности профессора и от должности ректора университета. Всё это подорвало здоровье учёного. Он ослеп, тяжело заболел. 24 февраля 1856 года Н.И. Лобачевский умер. Прошло ещё не менее 20 лет, прежде чем геометрия Н.И. Лобачевского завоевала права гражданства в математике.
Слайд 12
Казанский университет в 1830-е годы
Слайд 15
В последний год жизни (1855 г.)
Слайд 16
Вторая тропинка - из жизни замечательных людей.
1. Кому
из великих математиков принадлежат слова?
а) Математика-царица наук (Гаусс)
б) Математика - это язык, на котором говорят все точные науки (Лобачевский)
в) Математику уж затем учить надо, что она ум в порядок приводит (Ломоносов)
2. Какой русский писатель окончил математический факультет Московского университета? (Грибоедов)
3. Кто из великих русских писателей занимался составлением математических задач? (Толстой, Лермонтов)
4. Первая женщина-математик в России. Член-корреспондент Петербургской Академии наук. Одарённая писательница. (Софья Ковалевская)
5. Русский учёный, 19 лет был ректором Казанского университета, создатель неевклидовой геометрии. (Лобачевский)
Слайд 17
Третья тропинка - литературная.
К. Анкундинов
«Учёный кот»
басня
Слайд 18
У кошки маленький котёночек подрос.
-Как дальше быть? -
возник вопрос.
Ловить мышей - такая штука,
Что тут нужна теперь
наука.
Решила мать, что впору
Послать котёнка в школу.
И вот за партой в классе
Сидит пушистый Вася…
С усердием большим, как наказала мать,
Принялся кот науку постигать.
Он изучил до тонкости по темам
Строение мышей (по графикам и схемам).
Их чучела изготовлял из тряпок
В кружке «умелых лапок».
Решал, едва не плача,
Он про бассейн задачу
(Сколь выльется сметаны,
Когда открыты краны).
Был в геометрии как дома.
Знал доказательств остроту,
Тригонометрия знакома
Была прилежному коту.
Слайд 19
И через десять лет, науками богат,
Понёс домой наш
кот из школы аттестат…
В то время у какой-то горки
Мышонок
вылезал из норки,
Хоть Васька изучал мышиный род по книгам,
Исконного врага узнал он всё же мигом.
Но как его схватить?
Нельзя же прыгнуть сразу.
Тут надо применить
Научных знаний базу…
Вот неизвестного мышонка
За икс он принял очень тонко.
Затем в системе CGS
Нашёл его удельный вес.
V - скорость, ускоренье - а.
(А брызги сыплются с пера!)
По теореме Пифагора
Он путь нашёл довольно скоро,
Привёл ответы, глядя в книгу,
К логарифмическому виду,
Вписал последнюю строку
И приготовился к прыжку…
Слайд 20
Пока учёный кот над уравненьем бился,
Мышонок- неуч в
норке скрылся.
Запомните, друзья, соль истины такой:
Теория мертва без практики
живой.
Слайд 21
Четвёртая тропинка – горы Мозгодрома.
Кто лучше всех считает?
Поединок
трёх команд.
(16386-396):78+402·306-12=
Сумма двух чисел равна 330. Когда в большем
числе отбросили справа один нуль, то числа стали равными. Какие это числа?
Задача Михаила Юрьевича Лермонтова.
Он увлекался математикой, придумывал сам задачи.
“Задумайте число, прибавьте к нему 25, прибавьте ещё 125, отнимите 36, вычтите задуманное число, остаток умножьте на 5, полученное число разделите на 2”. После всех преобразований Лермонтов говорил, что ответ он знает, а вы?
Слайд 22
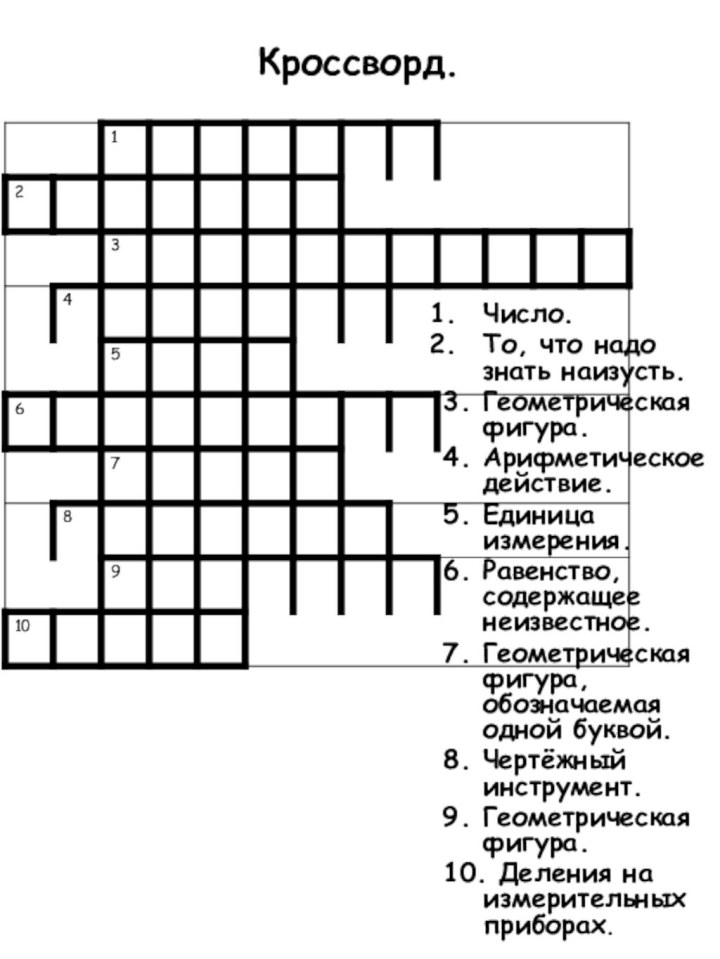
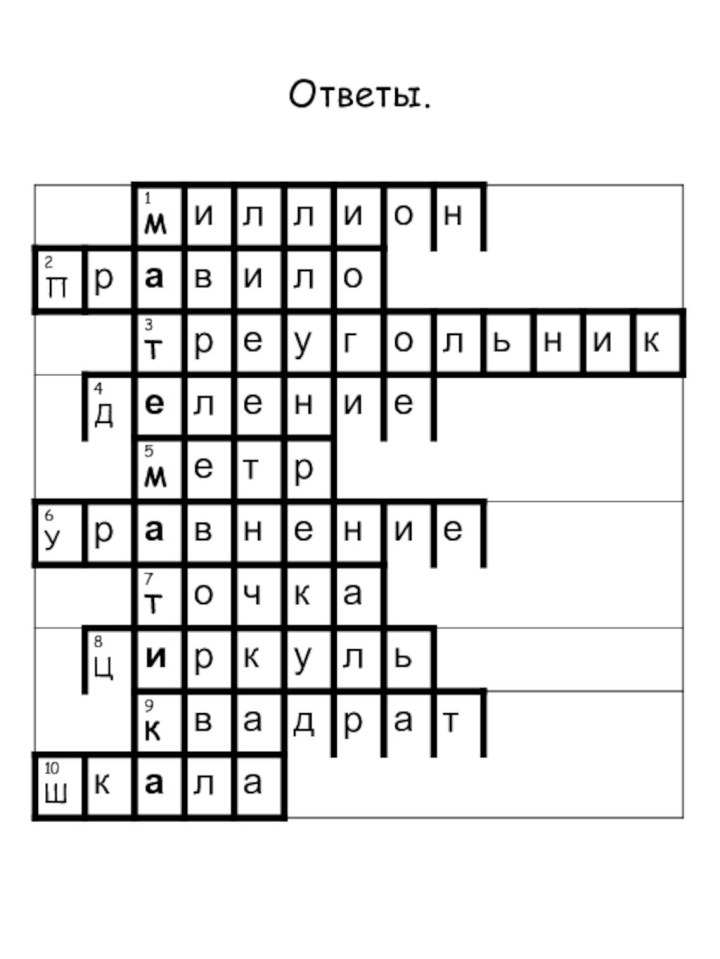
Кроссворд.
Число.
То, что надо знать наизусть.
3. Геометрическая
фигура.
4. Арифметическое действие.
5. Единица измерения.
6. Равенство, содержащее
неизвестное.
7. Геометрическая фигура, обозначаемая одной буквой.
8. Чертёжный инструмент.
9. Геометрическая фигура.
10. Деления на измерительных приборах.
Слайд 24
Пятая тропинка - математические софизмы.
Софизмом называется умышленно ложное
умозаключение, которое имеет видимость правильного. Каков бы ни был
софизм, он обязательно содержит одну или несколько замаскированных ошибок. Особенно часто в математических софизмах выполняются запрещённые действия или не учитываются условия применимости теорем, формул и правил.
В истории развития математики софизмы играли существенную роль. Они способствовали повышению строгости математических рассуждений.
Разбор софизмов развивает логическое мышление.
Например, 2×2 = 5.
Докажем это 4:4 = 5:5
4×(1:1) = 5×(1:1)
4 = 5
2×2 = 5.
Где ошибка?
Слайд 25
Ребята, впереди у вас много математических тропинок,
все
они ведут к удивительным открытиям и победам.
Книги – наши
лучшие помощники.