Слайд 2
Цель исследования
Расширение знаний о применении процентных
вычислений в задачах из различных сфер жизни человека.
Рассмотреть:
Проценты в повседневной жизни;
Проценты в организации сбалансированного питания школьника;
Проценты в ГИА и ЕГЭ;
Задачи с процентами на исторический сюжет;
Задачи с процентами с литературными сюжетами.
Предмет исследования - задачи на проценты, включенные в школьные учебники, экзамены.
Объект исследования - различные типы задач на проценты.
Слайд 3
Гипотеза исследования
Знание типов задач, и умение переводить
условие задачи с процентами, с учетом определенной классификации, дает
возможность решать любые задачи с процентами.
Задачи исследования:
Изучить специальную литературу по теме исследования;
Рассмотреть основные типы задач на проценты;
Показать применение понятия процентов при решении реальных задач в жизни человека;
Провести статистическое исследование;
Обобщить результат работы.
Создать сборник задач для учащихся «Проценты вокруг нас »
Методы:
Изучение литературы по теме;
Анкетирование;
Решение задач.
Слайд 4
Древний Вавилон
История возникновения процентов
В Древнем Вавилоне пользовались
шестидесятиричными дробями. Уже в клинописных табличках вавилонян содержатся задачи
на расчёт процентов. До нас дошли составленные вавилонянами таблицы процентов, которые позволяли быстро определять сумму процентных денег.
%
Слайд 5
Древний Рим
История возникновения процентов
Римляне называли процентами деньги,
которые платил должник заимодавцу за каждую сотню. Даже римский
сенат вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.
Слайд 6
Стевин Симон (1548-1620)
История возникновения процентов
Впервые опубликовал таблицы для
расчета процентов в 1584 г. Симон Стевин – инженер
из города Брюгге (Нидерланды).
Стевин известен замечательным разнообразием научных открытий, в том числе – особой записи десятичных дробей.
%
Слайд 7
История возникновения процентов
Знак «%» происходит, как полагают, от
итальянского слова cento (сто), которое в процентных расчетах часто
писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буквы t в наклонную черту произошел современный символ для обозначения процента.
Существует и другая версия возникновения этого знака. Предполагается, что этот знак произошел в результате нелепой опечатки.
45%
%
%
100%
99%
Слайд 8
Что такое процент?
Процент – сотая доля числа. 1
% = 1/100 = 0,01
Проценты – удобная относительная мера,
позволяющая оперировать с числами в привычном для человека формате, не зависимо от размера самих чисел. Это своего рода масштаб, к которому можно привести любое число.
Соотношение десятичных дробей и процентов:
0 = 0 %;
0,0007 = 0,07 %;
0,451 = 45,1 %;
1 = 100 %;
2 = 200 %.
Слайд 9
Разговорное употребление
«Работать за проценты» — работать за вознаграждение,
исчисляемое в зависимости от прибыли или оборота.
«На все сто
(процентов)» — всецело, полностью, целиком.
«Процентщик» — человек, ссужающий деньги под большие проценты, веритель.
Слайд 10
Виды задач на проценты
а) Нахождение процента от данного
числа.
Чтобы найти а % от в, нужно
б)Нахождение числа по
процентам.
Чтобы найти число, а % которого равны в, нужно
в) Нахождение процентного отношения чисел.
Чтобы найти процентное отношение чисел а и в, надо отношение этих чисел умножить на 100%, т.е.
99%
3%
%
100%
15%
%
Слайд 11
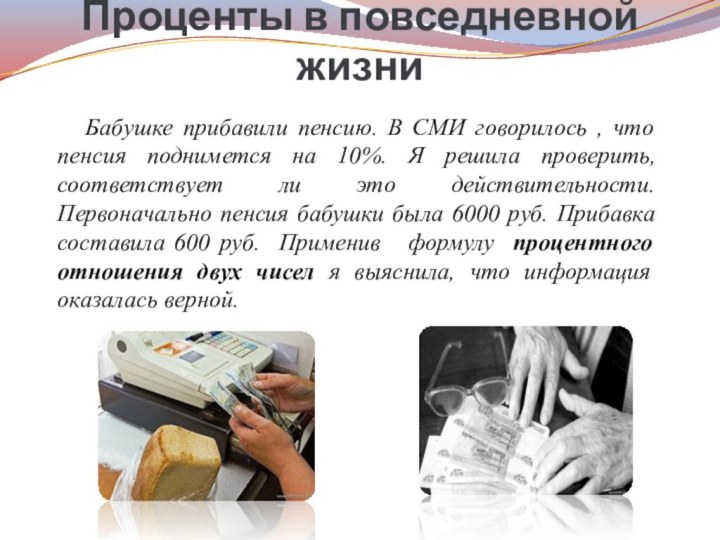
Проценты в повседневной жизни
Бабушке прибавили пенсию.
В СМИ говорилось , что пенсия поднимется на 10%.
Я решила проверить, соответствует ли это действительности. Первоначально пенсия бабушки была 6000 руб. Прибавка составила 600 руб. Применив формулу процентного отношения двух чисел я выяснила, что информация оказалась верной.
Слайд 12
Проценты в повседневной жизни
Для засолки огурцов
был нужен 9% раствор уксусной кислоты, в наличии был
70% раствор. Мама попросила меня посчитать сколько надо добавить воды в 20гр. 70% раствора, что бы получить 9% раствор.
Необходимо добавить 135,5 гр. воды. Огурцы получились на славу.
Слайд 13
Проценты в повседневной жизни
Мы пошли в
магазин покупать себе зимние сапоги. Родители выделили на их
покупку 2000 руб. В магазине мне понравились сапоги стоимостью 2300 руб. На них была скидка 25%. Мне стало любопытно, хватит ли у меня денег купить их? Применив формулу нахождения процентов от числа , получилось, что сапоги стоят 1725 руб. Я была рада. Денег хватало еще и на мороженое.
Слайд 14
Проценты в повседневной жизни
Я знаю, что в нашей
школе учится 56 человек, 27 из них девочки. Мне
стало интересно, сколько всего процентов от всех учеников составляют мальчики?
Применив формулу нахождения числа по проценту, я вычислила, что мальчиков в нашей школе больше, чем девочек на 4%.
Отличников 6 чел. - 11%,
Хорошистов 20 чел.- 36%.
Итог : всего учится на отлично и хорошо 47%. Предлагаю 3% учащихся нашей школы обратить на себя внимание и тогда будет не плохой результат к новому году.
Слайд 15
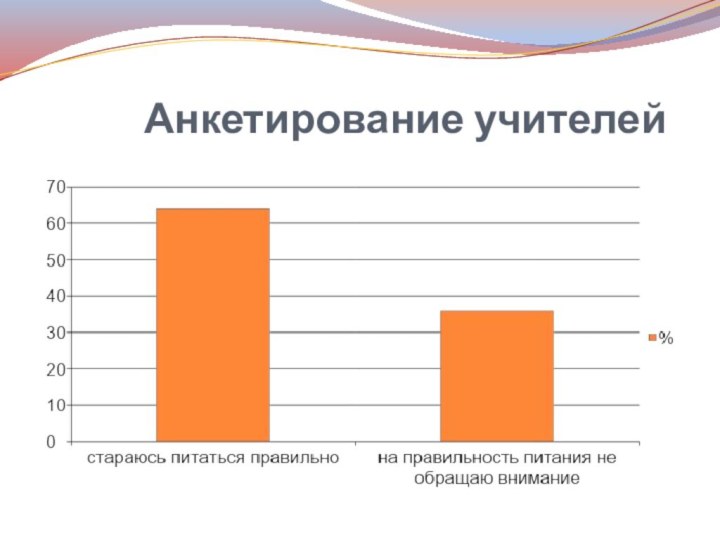
Проценты в организации питания школьника
Неправильно
питающийся человек сокращают себе жизнь на 15%. Определите какова
предположительная продолжительность жизни нынешних людей, употребляющих не здоровую пищу, если средняя продолжительность жизни в России 58 лет.
Решение:
15% = 0,15
58 ·0,15= 8,7 лет – сокращают жизнь
58 – 8,7 = 49,3 лет – продолжительность жизни неправильно питающегося человека
Слайд 17
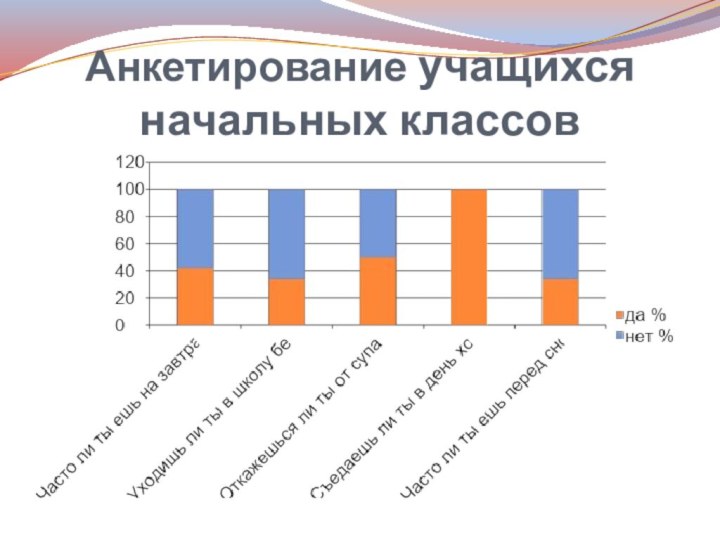
Анкетирование учащихся начальных классов
Слайд 18
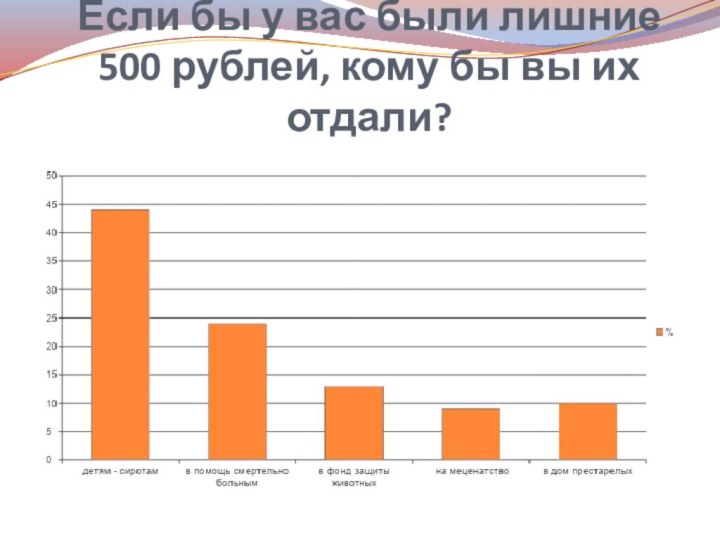
Если бы у вас были лишние 500 рублей,
кому бы вы их отдали?
Слайд 19
Проценты в ЕГЭ и ГИА
В сборнике
задач для ЕГЭ и ГИА тоже много задач на
проценты. Мы предлагаем вашему вниманию некоторые из них.
Слайд 20
К 120 г раствора, содержащего 80% соли, добавили
480 г раствора, содержащего 20 % той же соли.
Сколько процентов соли содержится в получившемся растворе?
Решение:
1) 0,8*120=96(г)- соли в первоначальном растворе;
2) 480*0,2=96(г) - соли во втором растворе;
3) ((96+96)/(120+480))*100%=32%-процентное содержание соли в получившемся растворе.
Ответ: 32%.
Слайд 21
Проценты в ЕГЭ и ГИА
При покупке
ребенку новых лыж с ботинками родителям пришлось заплатить на
35 % больше, чем два года назад, причем лыжи подорожали с тех пор на 20 %, а ботинки — на 70 %. Сколько процентов от стоимости лыж с ботинками составляла два года назад стоимость лыж?
Решение:
1/2x+1,7y=1,35(x+y),
Где х руб. – стоили лыжи два года назад.
y руб. – стоили ботинки два года назад.
y=3/7x;
x/(x+y)=x/(x+3/7x)=7/10
Ответ: 70%
Слайд 22
Задачи на исторический сюжет
Один небогатый римлянин
взял в долг у заимодавца 50 сестерциев. Заимодавец поставил
условие: « Ты вернешь мне в установленный срок 50 сестерциев и еще 20% от этой суммы». Сколько сестерциев должен отдать небогатый римлянин заимодавцу, возвращая долг?
Ответ:60 сестерциев.
Слайд 23
Задачи с литературными героями
В новелле О.
Бальзака «Гобсек» один из героев, господин Дервиль, взял у
ростовщика Гобсека сумму в 150000 франков сроком на 10 лет под 15 % годовых. Вычислите, какую сумму вернул Дервиль Гобсеку по происшествии этого срока.
Ответ:606833,6 франка.