Слайд 2
Среди множества пределов, которые
встречаются в математике и других дисциплинах, особое место занимают
по их значению два предела, которые называются замечательными.
К первому замечательному пределу относится предел
Х→0
Слайд 3
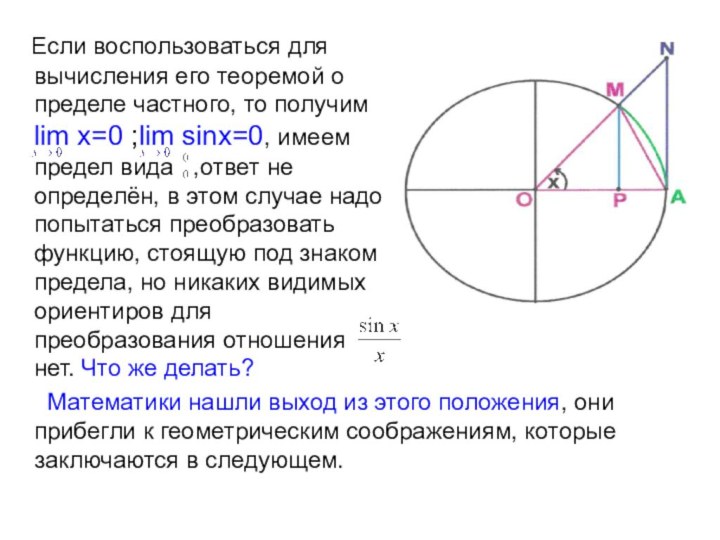
Если воспользоваться для вычисления его теоремой
о пределе частного, то получим lim x=0 ;lim sinx=0,
имеем предел вида ,ответ не определён, в этом случае надо попытаться преобразовать функцию, стоящую под знаком предела, но никаких видимых ориентиров для преобразования отношения нет. Что же делать?
Математики нашли выход из этого положения, они прибегли к геометрическим соображениям, которые заключаются в следующем.
Слайд 4
Возьмём окружность радиуса ОА = R
= 1 и некоторый угол Х с вершиной в
центре окружности (рис. 4). Проведём далее хорду АМ и касательную AN, пересекающую продолжение радиуса ОМ в точке N.
Из рисунка видно:
SΔAOM
SΔAOM = ½ OA · MP (2)
Sкр. сектора AOM= ½ OA·MA (3)
SΔAOM = ½ OA ·AN (4)
Представляя из (2) (3) и (4) в (1) получим:
OA · MP/2< OA · MA/2 < OA ·AN/2 (5)
Т.к. OA=R=1 после умножения на 2 получим: MP
Слайд 5
Т.к MP=sin x AN=tg x AM=x
поэтому (6) принимает вид:
sin x
или sin x
Т.к Х - острый угол, то sin x -величина положительная;
Разделив неравенства (7) на sin x получим
1< <
Или, взяв обратные отношения в этих неравенствах, будем иметь 1>sin x/x>cos x (8)
(поясним на примере: 1<5/2<7/2 – очевидно; возьмем обратные отношения 1>2/5>2/7)
Из тригонометрии известно, что если Х→0, то cos x→1. но т.к. отношение sin x/x согласно неравенству (8) заключено между единицей и cos x то оно и подавно стремится к единице.
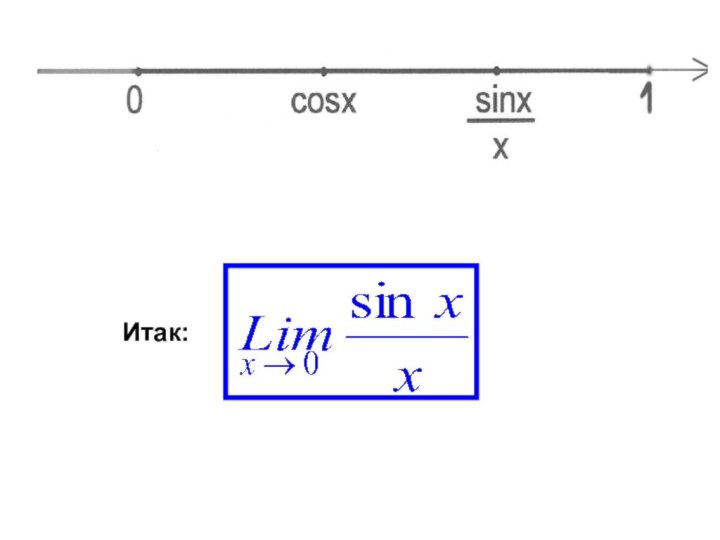
Это стремление отношения sin x/x к единице хорошо просматривается, если величины, содержащие в неравенстве (8) представить на координатной оси (рис.5)
Слайд 7
Почему же этот предел удостоился названия
замечательного?
Воспользуемся понятием предела функции: lim f (x)=a
f (x)-a=b
C учётом этого (*) можно переписать так:
(9) Умножая (9) на x, получим:sinx-x=b*x или sinx=x+b*x (10)
В правой части равенства (10) (по условию)-это бесконечно малая величина,
Слайд 8
b*x-,бесконечно малая функция 2го
порядка; пренебрегая этим слагаемым, получим: sinx x (*’)
Получили из равенства (*`) -Синусы малых углов примерно равны величинами самих углов, а это значит, что для нахождения синусов малых углов достаточно воспользоваться (*`), разумеется, что угол здесь измерен в радианах.
Возникает вопрос: каков диапазон углов, синусы которых можно находить по (*`)?
Слайд 9
Оказывается достаточно большой, так если Х∈[0;
6), то с точностью до 4-го знака после запятой
работает равенство sin x = x.
Пример: Х = 2°; sin2°≈2°(рад); тогда2°—Х рад180°—π радХ = 2π/180°=π/90°=3,14/90°=0,03488, получим, чтоsin2°=0,03488, точное значение sin2°=0,03489 (по МК)
Слайд 10
Если Х∈[6°; 12°), то sin x
= x с точностью до 3-го знака.
Пример:
Х = 10°;sin10°≈10(рад); тогда10°—Х рад180°—π радХ = 10π/180°=π/18°=3,14/18°=0,1744, получим, чтоsin10°=0,1744; точное значение sin10°=0,1744 (по МК)
Слайд 11
Если Х∈[12°; 20°), то sin x
= x с точностью до 2-го знака.
Пример:
Х = 18°;sin18°≈18(рад); тогда18°—Х рад180°—π радХ = 18π/180°=π/10°=3,14/10°=0,314, получим, чтоsin10°=0,314; точное значение sin18°=0,309 (по МК)
Слайд 12
промежутке до 200. К примеру, в треугольнике (Рис.6)
Тот факт, что синусы малых
углов можно заменить величинами самих углов, имеет непревзойдённое значение и при решении прямоугольных треугольников, когда острый угол заключён в
Слайд 13
известны (гипотенуза) и ,
требуется найти h.
Из соотношения
Если угол небольшой, то sina=a и тогда h=l*a
Из расчётов “ушёл” синус, оперируем только углами.
На сколько это важно – убедитесь при расчётах различных оптических систем, а также в механике при движении тел по наклонной плоскости с малыми углами наклона.
Возможность (*) ещё и в том, что с его помощью можно доказать, что
Слайд 14
откуда следует, что для малых углов tg x≈x
Углов точность понижается, другими словами диапазон углов, для которых
tg x, меньший, чем у синуса.
Слайд 16
1.Для нахождения синусов и тангенсов малых углов
можно обойтись без таблиц и вычислительной техники, для этого
достаточно данный угол выразить в радианной мере,
2.Тангенсы малых углов при расчётах можно заменить синусами.
3.Если угол небольшой, то при решении прямоугольных треугольников синусы можно заменить углами.
Слайд 17
Для подтверждения теоретического вывода
1го “замечательного’ предела можно убедиться в его истинности, выполнив
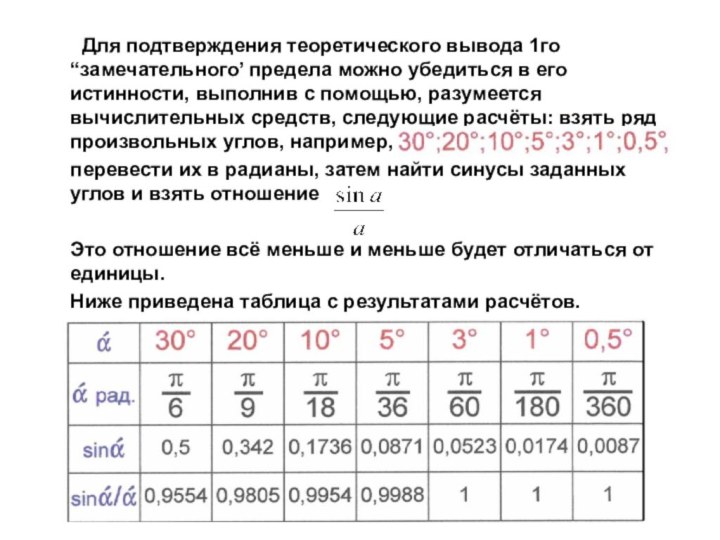
с помощью, разумеется вычислительных средств, следующие расчёты: взять ряд произвольных углов, например,
перевести их в радианы, затем найти синусы заданных углов и взять отношение
Это отношение всё меньше и меньше будет отличаться от единицы.
Ниже приведена таблица с результатами расчётов.
Слайд 18
Ко второму “Замечательному” пределу относится предел
функции
x→∞
В курсе высшей математике доказывается,
что предел (1+1/x)x при Х ∞ существует (он больше 2, но меньше 3) и выражается иррациональным числом, т. е.
2< <3
Х→∞
Слайд 19
Для пояснения сказанного составим
следующую таблицу выражения (1+1/x)x при возрастающих значениях Х:
х
1 2 5 10 100 1000
(1+1/x)x 2 2,25 2,49 2,59 2,705 2,713
Из таблицы видно, что по мере возрастания Х выражение (1+1/x)x также возрастает, замедляясь в росте.
Предел при Х ∞, равный приближенно 2,718, принято обозначать буквой е, которое называется числом Непера.
Джон Непер (1550 – 1617) шотландский математик, он был первым создателем таблиц логарифмов – натуральных, которые в математике называют НЕПЕРОВЫМИ.
= 2,71828….= е –
x→∞
число Непера
В прикладных дисциплинах это число называют экспонентой (exp) и записывают так: exp=2,71828….=е
exp (5х)=е5х;
exp (-2t)=e-2t.
Можно доказать, что для любой бесконечно малой функции α выражение (1+α)1/α , т. е. lim (1+α)1/α
α→0
Слайд 21
Возникает вопрос: почему этот предел
называют “замечательным”?
Во-первых, в математике число е
имеет очень важное значение, которое можно сравнить со значением числа π = 3,14. Как было отмечено в теории логарифмов, число е принимают за основание натуральных чисел, или Неперовых логарифмов, имеющих большое применение в математическом анализе, так как с их помощью многие формулы можно представить в более простом виде, чем при пользовании десятичными логарифмами.
Во – вторых, нет такой области в науке и технике, где можно было бы обойтись без числа е: многие параметры, которые характеризуют переменные процессы, изменяются по экспоненциальному закону, то есть по закону, связанному с числом Непера.