Слайд 2
Алгоритмы: основные понятия, примеры практической разработки
Интуитивное понятие алгоритма.
Под алгоритмом понимают точное предписание (набор инструкций) о выполнении
в определенной последовательности (порядке) некоторой системы операций для решения всех задач некоторого заданного типа.
Входные данные для задач одного типа
Вычислитель, пользующийся алгоритмом решения задачи данного типа
Результат
В математике серия однотипных задач считается решенной, когда для ее решения (при любых начальных данных) установлен алгоритм.
Слайд 3
Алгоритмы: основные понятия, примеры практической разработки
Простейшие алгоритмы -
правила выполнения основных арифметических действий для десятичных чисел. В
IX веке сформулированы Мухамедом бен Муссой по прозвищу Аль-Хорезми (сам термин «алгоритм» отдаленно напоминает его имя).
Согласно Аль-Хорезми, процедура сложения двух многозначных чисел разлагается в цепочку элементарных действий, при осуществлении которых вычислитель (исполнитель) обозревает лишь две цифры соответствующего разряда. Одна из этих цифр может быть снабженной специальной пометкой, указывающей на необходимость переноса единицы в следующий разряд.
Эти элементарные операции бывают двух типов:
запись соответствующей цифры суммы;
пометка о переносе над соседней слева цифрой.
При этом алгоритм предписывает надлежащий порядок выполнения этих операций: справа налево.
Слайд 4
Алгоритмы: основные понятия, примеры практической разработки
Формальный характер предписаний
(команд алгоритма), т.е. их независимость от содержания, вкладываемого в
используемые в операциях числа, дает возможность их применения для любых исходных данных.
Ключевые понятия.
Команда – это указание исполнителю совершить некоторое действие.
Исполнитель (вычислитель) – устройство или живой существо, которое выполняет по определенным правилам составленный алгоритм. Исполнитель, который не понимает цели алгоритма, называется формальным исполнителем.
Алгоритмом называется точная инструкция (набор команд) исполнителю, сформулированная в понятной для него форме и определяющая процесс достижения поставленной цели на основе имеющихся исходных данных за конечное число шагов.
Слайд 5
Алгоритмы: основные понятия, примеры практической разработки
Свойства алгоритма.
1. Универсальность
(массовость) - применимость алгоритма к различным наборам исходных данных.
2. Дискретность - процесс решения задачи по алгоритму разбит на отдельные действия.
3. Конечность - каждое из действий и весь алгоритм в целом обязательно завершаются.
4. Результативность - по завершении выполнения алгоритма обязательно получается конечный результат.
5. Выполнимость (эффективность) - результата алгоритма достигается за конечное число шагов.
6. Детерминированность (определенность) - алгоритм не должен содержать предписаний, смысл которых может восприниматься неоднозначно. Т.е. одно и то же предписание после исполнения должно давать один и тот же результат.
7. Последовательность – порядок исполнения команд должен быть понятен исполнителю и не должен допускать неоднозначности.
Слайд 6
Алгоритмы: основные понятия, примеры практической разработки
Классы алгоритмов.
-
вычислительные алгоритмы, работающие со сравнительно простыми видами данных, такими
как числа и матрицы, хотя сам процесс вычисления может быть долгим и сложным;
- информационные алгоритмы, представляющие собой набор сравнительно простых процедур, работающих с большими объемами информации (алгоритмы баз данных);
- управляющие алгоритмы, генерирующие различные управляющие воздействия на основе данных, полученных от внешних процессов, которыми алгоритмы управляют.
Классификация алгоритмов по типу передачи управления:
Основные (главные выполняемые программы) и вспомогательные (подпрограммы). Вспомогательный алгоритм должен быть снабжен таким заголовком, который позволяет вызывать этот алгоритм из других алгоритмов (например, основных).
Слайд 7
Алгоритмы: основные понятия, примеры практической разработки
Способы записи алгоритмов
-
Вербальный (словесный), когда алгоритм описывается на человеческом языке;
-
графический, когда алгоритм описывается с помощью набора графических изображений.
- символьный, когда алгоритм описывается с помощью специального набора символов (специального языка);
Словесная форма записи алгоритмов обычно используется для алгоритмов, ориентированных на исполнителя-человека. Команды такого алгоритма выполняются в естественной последовательности, если не оговорено противного.
Слайд 8
Алгоритмы: основные понятия, примеры практической разработки
Графическая запись с
помощью блок-схем осуществляется рисованием последовательности геометрических фигур, каждая из
которых подразумевает выполнение определенного действия алгоритма. Порядок выполнения действий указывается стрелками. Написание алгоритмов с помощью блок-схем регламентируется ГОСТом.
Слайд 9
Алгоритмы: основные понятия, примеры практической разработки
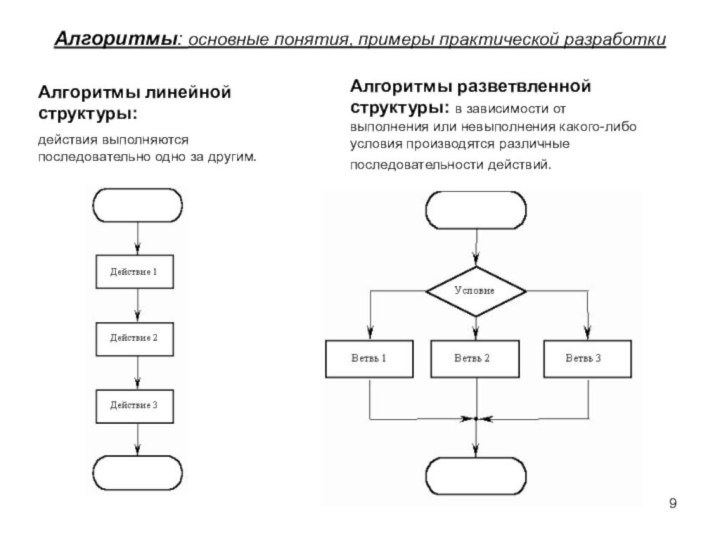
Алгоритмы линейной структуры:
действия выполняются последовательно одно за другим.
Алгоритмы разветвленной структуры: в
зависимости от выполнения или невыполнения какого-либо условия производятся различные последовательности действий.
Слайд 10
Алгоритмы: основные понятия, примеры практической разработки
Алгоритмы циклической структуры:
в зависимости от выполнения или невыполнения какого-либо условия выполняется
повторяющаяся последовательность действий, называющаяся телом цикла. Различают циклы с предусловием и постусловием:
Слайд 11
Алгоритмы: основные понятия, примеры практической разработки
Языки программирования содержат
операторы цикла со счетчиком. Они используются, когда изначально известно,
сколько итераций (проходов) цикла необходимо выполнить. Модель цикла со счетчиком может быть описана с помощью классического цикла с предусловием.
Инициализация переменной счетчика
Тело цикла
Изменение счетчика
Условие на значение счетчика
да
нет
Продолжение выполнения
Слайд 12
Алгоритмы: основные понятия, примеры практической разработки
Язык машинных команд

применялся до создания языков программирования высокого уровня (50-60 годы
прошлого века). В машине БЭСМ была принята трехадресная система команд. Каждая команда в этой системе представляла из себя последовательность четырех десятичных двухзначных чисел:
aa xx yy zz
где aa - указывало номер предписываемой операции; xx и yy - адреса двух ячеек, над
содержимым которых совершается данная операция; zz - определяло адрес ячейки, в которую необходимо поместить результат.
Последовательность цифр 01 11 12 15 представляет собой зашифрованную команду:
«Сложить (операция 01) числа из ячеек с адресами 11 и 12, результат поместить в ячейку с адресом 15».
Чтобы оперировать адресами хотя бы 255 ячеек памяти, размер самой ячейки в трехадресной команде (а также и ячеек с самими данными) должен быть как минимум 4 байта, по одному байту (8 бит) на каждую часть команды. Соответственно размер чисел с таким размером ячейки памяти мог достигать 31 двоичных разрядов для целых чисел (крайний левый бит, как правило отдавался под знак числа), т.е. максимальное целое число могло быть 232 – 1. Для действительных чисел еще один бит отдавался для десятичной точки, соответственно максимальная точность (размер мантиссы) мог составлять 29 двоичных разрядов.
Слайд 13
Алгоритмы: основные понятия, примеры практической разработки
1. АРИФМЕТИЧЕСКИЕ КОМАНДЫ:
А)

01 xx yy zz – Сложить число из ячейки
с адресом xx с числом из ячейки с адресом yy и сумму отправить в ячейку с адресом zz .
Б) 02 xx yy zz – Вычесть из числа из ячейки с адресом xx число из ячейки с адресом yy и разность отправить в ячейку с адресом zz.
В) 03 xx yy zz – Умножить число из ячейки с адресом xx с числом из ячейки с адресом yy и произведение отправить в ячейку с адресом zz.
Г) 04 xx yy zz – Разделить число из ячейки с адресом xx на число из ячейки с адресом yy и частное отправить в ячейку с адресом zz.
2. КОМАНДЫ ПЕРЕДАЧИ УПРАВЛЕНИЯ:
Д) 05 00 00 zz – Переходить к команде, хранящейся в ячейке с адресом zz (безусловная передача управления).
Е) 05 01 yy zz – Переходить к команде, хранящейся в ячейке с адресом zz при условии, что в ячейке с адресом yy хранится положительное число.
Ж) 05 02 yy zz – Переходить к команде, хранящейся в ячейке с адресом zz при условии, что в ячейке с адресом yy хранится отрицательное число.
3. КОМАНДА ОСТАНОВКИ:
00 00 00 00.
Команды выполнялись в том порядке, в каком они были записаны в ячейках памяти, если, конечно, данный порядок не менялся в результате выполнения команды передачи управления.
Слайд 14
Алгоритмы: основные понятия, примеры практической разработки
Псевдокод занимает промежуточное
место между естественным, машинным и формальным языком (языками программирования).
Структура программы на псевдокоде следующая.
прог имя (арг <список аргументов>)
линк список имен внешних подпрограмм;
лог список имен логических переменных;
цел список имен целых переменных;
вещ список имен вещественных переменных;
строка имя(длина);
массив имя[размерность] тип значений < лог | цел | вещ | строка (длина)>;
функция имя(параметры)
{
<тело функции>
возврат значение;
}
подпрог имя(параметры);
{
<тело подпрограммы>
}
нач
<выполняемое тело программы>
кон
Слайд 15
Алгоритмы: основные понятия, примеры практической разработки
1. Операторы ввода,

вывода
ввод (список переменных);
вывод («строка», список переменных);
2. Операторы цикла:
нц
пока (условие выполнения)
{
тело цикла
}
кц пока
// комментарии
нц до
{
тело цикла
}
кц до (условие завершения)
// комментарии
нц для (инициализация счетчика; условие завершения; шаг)
{
тело цикла
}
кц для
3. Условный оператор:
если (условие)
то {последовательность действий}
иначе {последовательность действий}
4. Операторы инкремент и декремент:
«++» увеличивает целую переменную на 1;
«--« уменьшает целую переменную на 1.
Используются:
знаки арифметических операций: «+», « - «, «/», «*» в выражениях, оператор присвоить «=».
В логических выражениях будут применяться следующие операторы «==» - равно, «!=» - не равно; «<» - меньше; «<=» меньше или равно; «>» - больше; «>=» - больше или равно.
Для объединения логических условий будем использовать логические операторы «И» - «&», «ИЛИ» - «||».
Чтобы присвоить логической переменной значения будем использовать литералы ИСТИНА или ЛОЖЬ.
Операторы будут отделяться «;». Группы операторов мы будем заключать в фигурные скобки «{» и «}».
Ключевые слова отличаются от имен переменных русским написанием и снабжаются подчеркиванием.
Слайд 16
Алгоритмы: основные понятия, примеры практической разработки
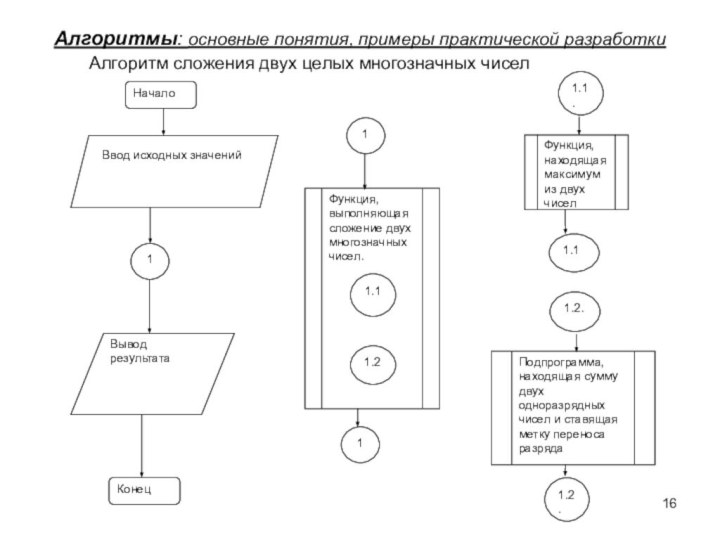
Алгоритм сложения двух
целых многозначных чисел
Ввод исходных значений
1
1
1
1.1.
1.1
1.2.
1.2.
Функция, выполняющая сложение двух многозначных
чисел.
Вывод результата
Начало
Конец
1.1
1.2
Функция, находящая максимум из двух чисел
Подпрограмма, находящая сумму двух одноразрядных чисел и ставящая метку переноса разряда
Слайд 17
Алгоритмы: основные понятия, примеры практической разработки
подпрог sum2(rs строка(1),

rq строка(1), rr строка(1), f лог)
{ f = ЛОЖЬ;
если
(rs == “0”) то {rr = rq;}
если (rq == “0”) то {rr = rs;}
если ((rs == “1”) & (rq == “1”)) то {rr = “2”;}
если ( ( ((rs == “1”) & (rq == “2”)) ) || ( ((rs == “2”) & (rq == “1”)) ) ) то {rr = “3”;}
если ( ( ((rs == “1”) & (rq == “3”)) ) || ( ((rs == “3”) & (rq == “1”)) ) ) то {rr = “4”;}
если ( ( ((rs == “1”) & (rq == “4”)) ) || ( ((rs == “4”) & (rq == “1”)) ) ) то {rr = “5”;}
если ( ( ((rs == “1”) & (rq == “5”)) ) || ( ((rs == “5”) & (rq == “1”)) ) ) то {rr = “6”;}
если ( ( ((rs == “1”) & (rq == “6”)) ) || ( ((rs == “6”) & (rq == “1”)) ) ) то {rr = “7”;}
если ( ( ((rs == “1”) & (rq == “7”)) ) || ( ((rs == “7”) & (rq == “1”)) ) ) то {rr = “8”;}
если ( ( ((rs == “1”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “1”)) ) ) то {rr = “9”;}
если ( ( ((rs == “1”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “1”)) ) ) то {rr = “0”; f = ИСТИНА;}
если ( ((rs == “2”) & (rq == “2”)) ) то {rr = “4”; }
если ( ( ((rs == “2”) & (rq == “3”)) ) || ( ((rs == “3”) & (rq == “2”)) ) ) то {rr = “5”; }
если ( ( ((rs == “2”) & (rq == “4”)) ) || ( ((rs == “4”) & (rq == “2”)) ) ) то {rr = “6”; }
если ( ( ((rs == “2”) & (rq == “5”)) ) || ( ((rs == “5”) & (rq == “2”)) ) ) то {rr = “7”; }
если ( ( ((rs == “2”) & (rq == “6”)) ) || ( ((rs == “6”) & (rq == “2”)) ) ) то {rr = “8”; }
если ( ( ((rs == “2”) & (rq == “7”)) ) || ( ((rs == “7”) & (rq == “2”)) ) ) то {rr = “9”; }
если ( ( ((rs == “2”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “2”)) ) ) то {rr = “0”; f = ИСТИНА;}
если ( ( ((rs == “2”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “2”)) ) ) то {rr = “1”; f = ИСТИНА;}
если ( ((rs == “3”) & (rq == “3”)) ) то {rr = “6”; }
если ( ( ((rs == “3”) & (rq == “4”)) ) || ( ((rs == “4”) & (rq == “3”)) ) ) то {rr = “7”; }
если ( ( ((rs == “3”) & (rq == “5”)) ) || ( ((rs == “5”) & (rq == “3”)) ) ) то {rr = “8”; }
если ( ( ((rs == “3”) & (rq == “6”)) ) || ( ((rs == “6”) & (rq == “3”)) ) ) то {rr = “9”; }
если ( ( ((rs == “3”) & (rq == “7”)) ) || ( ((rs == “7”) & (rq == “3”)) ) ) то {rr = “0”; f = ИСТИНА;}
если ( ( ((rs == “3”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “3”)) ) ) то {rr = “1”; f = ИСТИНА;}
если ( ( ((rs == “3”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “3”)) ) ) то {rr = “2”; f = ИСТИНА;}
Слайд 18
Алгоритмы: основные понятия, примеры практической разработки
если ( ((rs

== “4”) & (rq == “4”)) ) то {rr
= “8”; }
если ( ( ((rs == “4”) & (rq == “5”)) ) || ( ((rs == “5”) & (rq == “4”)) ) ) то {rr = “9”; }
если ( ( ((rs == “4”) & (rq == “6”)) ) || ( ((rs == “6”) & (rq == “4”)) ) ) то {rr = “0”; f = ИСТИНА;}
если ( ( ((rs == “4”) & (rq == “7”)) ) || ( ((rs == “7”) & (rq == “4”)) ) ) то {rr = “1”; f = ИСТИНА;}
если ( ( ((rs == “4”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “4”)) ) ) то {rr = “2”; f = ИСТИНА;}
если ( ( ((rs == “4”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “4”)) ) ) то {rr = “3”; f = ИСТИНА;}
если ( ((rs == “5”) & (rq == “5”)) ) то {rr = “0”; f = ИСТИНА;}
если ( ( ((rs == “5”) & (rq == “6”)) ) || ( ((rs == “6”) & (rq == “5”)) ) ) то {rr = “1”; f = ИСТИНА;}
если ( ( ((rs == “5”) & (rq == “7”)) ) || ( ((rs == “7”) & (rq == “5”)) ) ) то {rr = “2”; f = ИСТИНА;}
если ( ( ((rs == “5”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “5”)) ) ) то {rr = “3”; f = ИСТИНА;}
если ( ( ((rs == “5”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “5”)) ) ) то {rr = “4”; f = ИСТИНА;}
если ( ((rs == “6”) & (rq == “6”)) ) то {rr = “2”; f = ИСТИНА;}
если ( ( ((rs == “6”) & (rq == “7”)) ) || ( ((rs == “7”) & (rq == “6”)) ) ) то {rr = “3”; f = ИСТИНА;}
если ( ( ((rs == “6”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “6”)) ) ) то {rr = “4”; f = ИСТИНА;}
если ( ( ((rs == “6”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “6”)) ) ) то {rr = “5”; f = ИСТИНА;}
если ( ((rs == “7”) & (rq == “7”)) ) то {rr = “4”; f = ИСТИНА;}
если ( ( ((rs == “7”) & (rq == “8”)) ) || ( ((rs == “8”) & (rq == “7”)) ) ) то {rr = “5”; f = ИСТИНА;}
если ( ( ((rs == “7”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “7”)) ) ) то {rr = “6”; f = ИСТИНА;}
если ( ((rs == “8”) & (rq == “8”)) ) то {rr = “6”; f = ИСТИНА;}
если ( ( ((rs == “8”) & (rq == “9”)) ) || ( ((rs == “9”) & (rq == “8”)) ) ) то {rr = “7”; f = ИСТИНА;}
если ( ((rs == “9”) & (rq == “9”)) ) то {rr = “8”; f = ИСТИНА;}
}
«вычислитель», обозревая два символа (цифры) rs и rq производит их «сложение», т.е. каждой возможной паре этих символов ставит в соответствие символ rr, являющийся результатом суммирования и переводит, если это необходимо, метку переноса разряда (логическая переменная f) в состояние «ИСТИНА».
Слайд 19
Алгоритмы: основные понятия, примеры практической разработки
Вспомогательная функция, находящая

максимальное из двух целых многозначных чисел при условии, что
числа представлены как массивы строк длины 1, а «вычислитель» не умеет производить сравнение целых значений.
функция max(s[*] строка(1), цел n, q[*] строка(1), цел m)
{
цел i;
если (n > m) то { возврат s;}
иначе { возврат q;}
если (n == m) то { i =1;
нц пока ( (s[i] == q[i]) & (i < n+1) )
{
i++;
}
кц пока
если (i == n+1) то { возврат s;}
иначе {
если ( (s[i] = “9”) ||
( (s[i] = “8”) & (q[i]) != “9”) ) ||
( (s[i] = “7”) & (q[i]) != “9”) & (q[i]) != “8”) ) ||
( (s[i] = “6”) & (q[i]) != “9”) & (q[i]) != “8”) & (q[i]) != “7”) ) ||
( (s[i] = “5”) & (q[i]) != “9”) & (q[i]) != “8”) & (q[i]) != “7”) & (q[i]) != “6”) ) ||
( (s[i] = “4”) & (q[i]) != “9”) & (q[i]) != “8”) & (q[i]) != “7”) & (q[i]) != “6”) & (q[i]) != “5”) ) ||
( (s[i] = “3”) & (q[i]) != “9”) & (q[i]) != “8”) & (q[i]) != “7”) & (q[i]) != “6”) & (q[i]) != “5”) & (q[i]) != “4”) ) ||
( (s[i] = “2”) & (q[i]) != “9”) & (q[i]) != “8”) & (q[i]) != “7”) & (q[i]) != “6”) & (q[i]) != “5”) & (q[i]) != “4”) & q[i]) != “3”)) ||
( (s[i] = “1”) & (q[i]) != “9”) & (q[i]) != “8”) & (q[i]) != “7”) & (q[i]) != “6”) & (q[i]) != “5”) & (q[i]) != “4”) & q[i]) != “3”) & (q[i]) != “2”) )
) то { возврат s;}
иначе { возврат q;}
}
}
При нашем предположении о неумении исполнителя воспринимать значения чисел как числа и производить с ними арифметические и логические операции НЕОБХОДИМО написать вспомогательные функции для выполнения указанных операций псевдокода, поскольку значения целых переменных i, n, m – должны быть представлены как массивы односимвольных строк также, как переменные s и q. Помимо этого, необходимо иметь функцию вычисляющую текущую размерность этих массивов.
Слайд 20
Алгоритмы: основные понятия, примеры практической разработки
Функция, которая, используя
описанную выше подпрограмму и функцию поиска максимума, вычисляет сумму
двух многозначных целых чисел.
функция sum(s[*] строка(1), цел n, q[*] строка(1), цел m)
{
цел j;
массив fl[max(s, n, q, m)+1] лог;
массив rs[max(s, n, q, m)+1] строка(1);
массив rq[max(s, n, q, m)+1] строка(1);
массив rr[max(s s, n, q, m)+1] строка(1);
// блок инициализации рабочих массивов. Поскольку при сложении может появиться дополнительный разряд слева, размерности рабочих массивов прибавляются на 1.
j=1;
нц пока (j <= (max(s, n, q, m)+1)
{
rs[j] = “0”; rq[j] = “0”;
j=j++;
}
кц пока
j =0;
нц пока (j <= n+1)
{
rs[max(s, n, q, m)+1-j] = s[n-j];
j=j++;
}
кц пока
j = 0;
нц пока (j <= m+1)
{
rq[max(s, n, q, m)+1-j] = q[m-j];
j=j++;
}
кц пока
Слайд 21
Алгоритмы: основные понятия, примеры практической разработки
// вычисляем сумму
крайних правых цифр
sum2(rs[max(s, n, q, m)+1], rq[max(s, n, q,
m)+1], rr[max(s, n, q, m)+1], fl[max(s, n, q, m)+1]);
// имея значения суммы и метку переноса разряда, вычисляем следующие справа налево
// суммы цифр
нц для (j= max(s, n, q, m); j <=1; j--)
{
sum2(rs[j], rq[j], rr[j], fl[j]);
// учитываем перенос разряда, если необходимо
если (fl[j+1]) то
{
если (rr[j] == “0”) то {rr[j] = “1”; }
если (rr[j] == “1”) то {rr[j] = “2”; }
если (rr[j] == “2”) то {rr[j] = “3”; }
если (rr[j] == “3”) то {rr[j] = “4”; }
если (rr[j] == “4”) то {rr[j] = “5”; }
если (rr[j] == “5”) то {rr[j] = “6”; }
если (rr[j] == “6”) то {rr[j] = “7”; }
если (rr[j] == “7”) то {rr[j] = “8”; }
если (rr[j] == “8”) то {rr[j] = “9”; }
если (rr[j] == “9”) то {rr[j] = “0”; fl[j] = ИСТИНА;}
}
}
кц для
// убираем возможные лишние нули слева
если (rr[1] == “0”)
то {
j = 1;
нц пока (j <= max(s, n, q, m))
{
rr[j] = rr[j+1];
j=j++;
}
кц пока
}
возврат rr;
}
Слайд 22
Алгоритмы: основные понятия, примеры практической разработки
Исходные данные (два
числа) считываются потоком посимвольно, символ пробел “ ” означает
конец числа в потоке. Тогда можно написать подпрограмму, которая считывает строку символов до первого пробела и заносит его в массив строк длины 1 размерности n.
подпрог inp(s[*] строка(1), цел n)
{
цел i;
строка ss(1);
i=0; ss=”’;
нц пока (ss != “ ”)
{
ввод (ss);
i++;
s[i] = ss;
}
кц пока
n = i--;
}
Программа, которая использует все разработанные ранее подпрограммы и функции и реализует алгоритм сложения двух чисел, считанных их входного потока данных (согласно блок-схеме).
прог p1(арг )
линк inp(),max(), sum2(), sum();
нач
цел n1,n2;
массив sv[*] строка(1);
массив qv[*] строка(1);
массив rv[*] строка(1);
inp(sv,n1);
inp(sq,n2);
rv= sum(sv,n1,sq, n2);
вывод (“Cумма”, rv);
кон
Слайд 23
Алгоритмы: основные понятия, примеры практической разработки
Пусть алгоритм сложения
двух целых чисел реализован с помощью функции СУММ(цел x,
цел y), которая принимает на входе два целых числа и выдает на выходе их сумму (целое число). Тогда фрагмент программы, которая выполняет умножение двух целых чисел n и m можно представить следующим образом.
функция УМН(цел n, цел m)
{
цел j, rez;
rez=0;
j=1;
нц пока (j <= m)
{
rez = СУММ(rez, n); // rez = rez + n;
j++;
}
кц пока
возврат rez;
}
Если функция СУММ() фактически имитирует работу оператора «+», то написанная выше функция УМН() – является аналогом оператора «*».
Слайд 24
Алгоритмы: основные понятия, примеры практической разработки
Алгоритм Евклида
Решает все
задачи следующего типа:
Для двух данных натуральных чисел а и
b найти их наибольший делитель.
Очевидно, что различных задач такого типа существует столько, сколько имеется различных пар чисел а и b .
Словесная форма записи алгоритма.
Указание 1. Обозревай два числа: а и b . Переходи к Указанию 2.
Указание 2. Сравни обозреваемые числа (либо а == b , либо а > b , либо а < b ). Переходи к Указанию 3.
Указание 3. Если обозреваемые числа равны (а == b ), то каждое из них дает искомый результат. Процесс вычислений остановить. Если числа не равны, то переходи к Указанию 4.
Указание 4. Если а < b , то переставь их местами и продолжай обозревать их. Переходи к Указанию 5.
Указание 5. Вычитай второе из обозреваемых чисел из первого и обозревай два числа: вычитаемое и остаток. Переходи к Указанию 2.
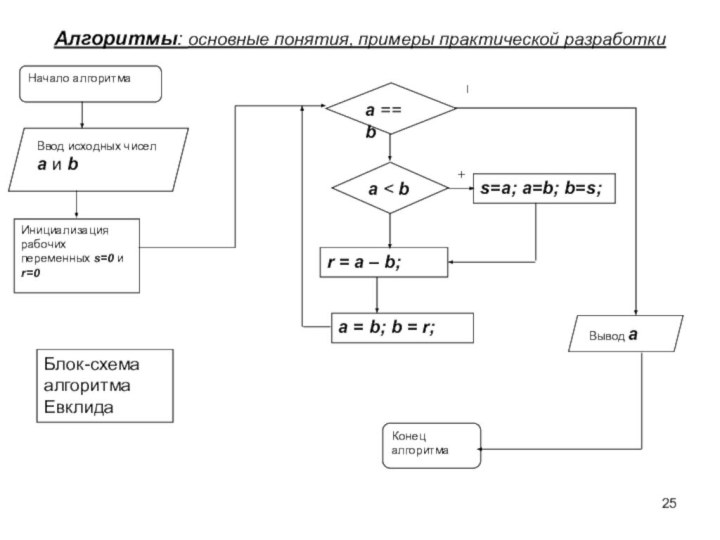
Слайд 25
Алгоритмы: основные понятия, примеры практической разработки
Ввод исходных чисел
а и b
Начало алгоритма
Инициализация рабочих переменных s=0 и
r=0
а == b
а < b
r = a – b;
s=a; a=b; b=s;
a = b; b = r;
Вывод а
Конец алгоритма
Блок-схема алгоритма Евклида
Слайд 26
Алгоритмы: основные понятия, примеры практической разработки
Ввод исходных чисел
а и b
Начало алгоритма
Инициализация рабочих переменных s=0 и
r=0
а != b
а < b
a = a – b;
b = b – a;
Вывод а
Конец алгоритма
Блок-схема алгоритма Евклида (упрощение)
Слайд 27
Алгоритмы: основные понятия, примеры практической разработки
Программа на языке
машинных команд, реализующая алгоритм Евклида.
Пусть исходные данные (числа a
и b) помещены в ячейки с адресами 12 и 13 соответственно, ячейки с адресами 14 и 15 будем использовать для промежуточных вычислений, а результат после остановки машины должен оказаться в ячейке с адресом 15.
Слайд 28
Алгоритмы: основные понятия, примеры практической разработки
Если a –
b = 0 (т.е. a = b), то команды
03 и 04 об условной передаче управления игнорируются (пропускаются) и выполняется команда 05, т.е. происходит остановка машины. К этому моменту в ячейке 15 находится искомый результат.
Если a – b < 0 (т.е. a < b), то команда 03 передает управление команде 06, которая вместе со следующей за ней командой 07 переставляет местами числа a и b в ячейках 12 и 13, потом команда 08 обеспечивает безусловный переход к команде 01 и начинается следующий цикл работы алгоритма.
Если a – b > 0 (т.е. a > b), то команда 03 пропускается, а следующая за ней команда 04, передает управление команде 09. Команды 09 и 10 пересылают в ячейки 12 и 13 прежнее вычитаемое и остаток от предыдущей разности, т.е. числа b и a – b. Затем команда 11 обеспечивает безусловный переход к команде 01 и начинается следующий цикл работы алгоритма.
После выполнения первых двух команд:
Слайд 29
Алгоритмы: основные понятия, примеры практической разработки
функция НОД(цел n,
цел m)
{
нц пока (n != m)
{
если (n > m) то {n = n – m;}
иначе {m = m – n;}
}
кц пока
возврат n;
}
прог p2(арг )
линк НОД();
{
нач
цел n1, n2, n3;
ввод n1, n2;
n3 = НОД (n1, n2);
вывод («результат», n3);
кон
}
Функция, нахождения НОД двух целых чисел
Программа, реализующая алгоритм в соответствии с упрощенной блок-схемой
Слайд 30
Алгоритмы: основные понятия, примеры практической разработки
Поиск максимума в

массиве чисел
Словесная форма записи.
Указание 1. Установи значение счетчика
в 1, переходи к указанию 2.
Указание 2. Установи значение результата, равное первому числу (элементу массива), переходи к Указанию 3.
Указание 3. Увеличь значение счетчика на 1, переходи к Указанию 4.
Указание 4. Сравни значение счетчика и количества чисел (размерность массива), переходи к указанию 5.
Указание 5. Если значение счетчика больше заданного количества чисел (размерности массива), то остановка. Иначе переходи к указанию 6.
Указание 6. Сравни значения результата и числа с номером, соответствующим текущему значению счетчика (текущего элемента массива), переходи к указанию 7.
Указание 7. Если значение результата меньше или равно значению числа с номером, соответствующим текущему значению счетчика (текущего элемента массива), то переходи к указанию 8, иначе переходи к указанию 9.
Указание 8. Присвой результату значение числа с номером, соответствующим текущему значению счетчика (текущего элемента массива), переходи к указанию 9.
Указание 9. Переходи к Указанию 3.
Слайд 31
Алгоритмы: основные понятия, примеры практической разработки
Счетчик = 1;
Результат
= а[1];
Результат = a[Счетчик];
Счетчик++;
Счетчик > N
нет
Результат
данного алгоритма на языке машинных команд «в лоб», т.е. выполнения N-1 раз двух операций: сравнение текущего элемента массива с промежуточным значением результата и присвоения в случае выполнения условия «<» значения текущего элемента промежуточному результату, необходимо, помимо N ячеек для хранения элементов массива выделить 4*(N-1)+1 ячеек памяти для размещения всех необходимых команд. При этом очевидно, что любое изменение исходных данных (массива чисел) приведет к необходимости переписывать эту программу заново.
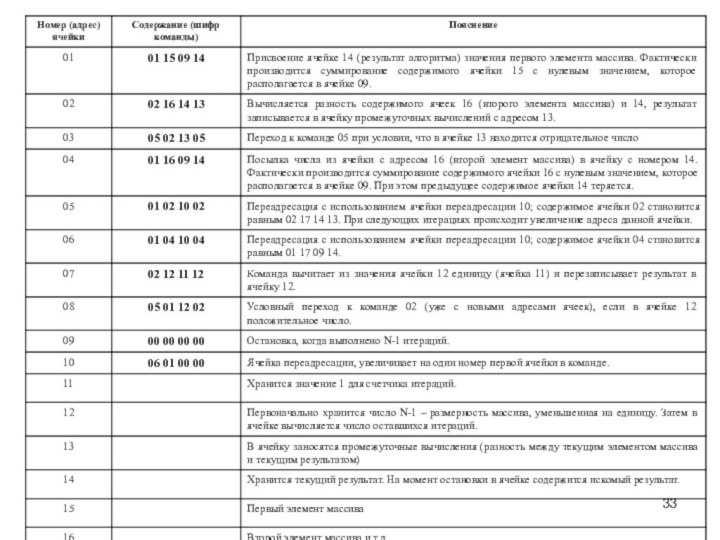
Слайд 32
Алгоритмы: основные понятия, примеры практической разработки
Для реализации циклических
алгоритмов в языке машинных команд предусмотрены так называемые команды
переадресации, с помощью которых можно запрограммировать повторяющиеся операции с использованием фиксированного набора ячеек. Условимся, что команды переадресации будут маркироваться числом 06 и их смысл будет заключаться в покомпонентном изменении адресов ячеек, участвующих в изменяемой команде. Например, если во вспомогательной ячейке переадресации с адресом 77 помещено значение 06 01 02 00, а исходная ячейка 33 имеет значение 02 16 20 05, то при выполнении команды переадресации 01 33 77 33 значение переадресованной ячейки 33 станет равным 02 17 22 05.
Пусть в ячейке 12 расположено значение размерности массива N, уменьшенное на единицу (N-1), в ячейке 13 результаты промежуточных вычислений, в ячейке 14 - искомый результат, с 15 ячейки размещены элементы массива.
Слайд 34
Алгоритмы: основные понятия, примеры практической разработки
функция МАКСМАС(цел n,
массив а[n] цел )
{
цел i, rez;
i = 2; rez
= a[1];
нц пока (i <= n)
{
если (rez < a[i]) то {rez=a[i];}
i++;
}
кц пока
возврат rez;
}
Алгоритм поиска максимума в массиве чисел на псевдокоде
Замечание. Если в условном операторе (указании 7) выполнить строгое сравнение, то алгоритм приведет к нахождению первого из встреченных максимальных значений набора чисел (элементов массива). В общем случае в массиве могут быть равные значения элементов. Если неравенство нестрогое – «<=» , то будет найден последний из равных максимальных значений. Хотя, несомненно, и в том и другом случае мы получим один и тот же числовой результат, фактически это могут быть разные элементы набора чисел (массива).
Слайд 35
Алгоритмы: основные понятия, примеры практической разработки
Сортировка – упорядочение

элементов в списке.
Метод «пузырька».
Самый популярный и достаточно медленный
вид сортировки. Основан на методе перестановок, т.е. в данном алгоритме осуществляется постоянное сравнение текущего элемента с другими элементами и перестановка их при необходимости.
Алгоритм состоит из двух вложенных циклов. Внешний цикл задает область поиска (диапазон индексов), а внутренний цикл внутри этого диапазона выполняет сравнение и перестановку элементов массива.
На первом проходе внешнего цикла первый элемент сравнивается попарно со всеми остальными элементами, начиная со второго. При этом, если выполняется условие «>», то элементы переставляются местами и сравнения обновленного значения первого элемента массива с оставшимися элементами продолжаются до тех пор, пока внутренний цикл не дойдет до последнего элемента. В результате на месте первого элемента окажется минимальное среди всех значений. Второй проход внешнего цикла сокращает область действия внутреннего цикла – первый элемент уже стоит на своем месте. Происходят сравнения второго элемента массива с последующими и при необходимости замены их местами. И так далее. После n-1 проходов внешнего цикла (n размер массива) на последнем месте в массиве остается только один (максимальный) элемент и алгоритм завершается.
1/2*n*(n-1) - число сравнений.
3/4*n*(n-1) - среднее число перестановок.
3/2*n*(n-1) - максимальное возможное число перестановок.
Слайд 36
Алгоритмы: основные понятия, примеры практической разработки
Исходный массив -

{15.0, -3.0, 10.0, 5.0, -9.0}.
1. Первый проход внешнего цикла:
произведено 2 замены и на первом месте оказалось минимальное значение среди всех элементов массива – «-9.0».
{-3.0, 15.0, 10.0, 5.0, -9.0} – первая замена 15 на -3;
{-3.0, 15.0, 10.0, 5.0, -9.0} – замены нет;
{-3.0, 15.0, 10.0, 5.0, -9.0} – замены нет;
{-9.0, 15.0, 10.0, 5.0, -3.0} – вторая замена -3 на -9.
2. Второй проход внешнего цикла: произведено 3 замены и на втором месте слева оказался минимальный из оставшихся элементов массива – «-3.0».
{-9.0, 10.0, 15.0, 5.0, -3.0} – первая замена 15 на 10.
{-9.0, 5.0, 15.0, 10.0, -3.0} – вторая замена 10 на 5.
{-9.0, -3.0, 15.0, 10.0, 5.0} – третья замена 5 на -3.
3. Третий проход внешнего цикла: производено 2 замены.
{-9.0, -3.0, 10.0, 15.0, 5.0} – первая замена 10 на 15.
{-9.0, -3.0, 5.0, 15.0, 10.0} – вторая замена 5 на 10.
4. На четвертом (последнем) проходе внешнего цикла произведена 1 замена Это привело к получению искомого результата:
{-9.0, -3.0, 5.0, 10.0, 15.0}.
Массив отсортирован по возрастанию.
Слайд 37
Алгоритмы: основные понятия, примеры практической разработки
Блок-схема алгоритма «пузырьковой»
сортировки
I=1;
J= I +1;
I > N-1
J > N
I++;
D =
A[J];
A[J] = A[I];
A[I] = D;
A[J] < A[I]
J++;
Конец
–
+
+
–
–
+
функция СОРТ1(цел n, массив а[n] цел )
{
цел i, j, k;
i = 1;
нц пока (i <= n-1)
{
j= i + 1;
нц пока (j <= n)
{
если (a[j] < a[i]) то {k = a[i]; a[i] = a[j]; a[j] = k;}
j++;
}
кц пока // по j
i++;
}
кц пока // по i
возврат a;
}
Задание: записать алгоритм сортировки в словесной форме (в виде указаний) и на языке машинных команд.
Слайд 38
Алгоритмы: основные понятия, примеры практической разработки
Рассмотренные нами алгоритмы
относятся к группе так называемых вычислительных алгоритмов. На самом
деле разрабатываются алгоритмы решения различных задач, в том числе и логических. Например, можно предложить схемы решения таких известных задач-головоломок, как решение игры 15, поиск кратчайшего пути в лабиринте (задача Тезей и Минотавр), а также разработать достаточно эффективные алгоритмы игры в шашки, шахматы и др.
Создание эффективных алгоритмов, как и доказательство отсутствия разрешающего алгоритма для того или иного типа задач, является одной из ключевых проблем математики и сродни ИСКУССТВУ.
Слайд 39
Алгоритмы: основные понятия, примеры практической разработки
Дональд Кнут «Искусство
программирования», The Art of Computer Programming,. — 2-е изд.
— М.: «Вильямс», 2007. — 824 с.
В ней, в томе 3 «Сортировка и поиск», описывается большинство известных типов алгоритмов сортировки.



























![Алгоритм, основные понятия, написание алгоритмов Алгоритмы: основные понятия, примеры практической разработкиСчетчик = 1;Результат = а[1];Результат = a[Счетчик];Счетчик++;Счетчик > NнетРезультат](/img/tmb/6/577293/a724e29f191d7b1a44a1619e8be1d8f8-720x.jpg)

![Алгоритм, основные понятия, написание алгоритмов Алгоритмы: основные понятия, примеры практической разработкифункция МАКСМАС(цел n, массив а[n] цел ){ цел](/img/tmb/6/577293/cfc9911b1a3851295c4a439f1dc01ec2-720x.jpg)