- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Введение в логику
Содержание
- 2. ПланАксиомы теории множеств (повт.)Трудности с полнотойЛогика высказываний. Синтаксис и семантика
- 3. Аксиомы теории множеств (повт.)Существование множеств x y
- 4. Один из способов Построение каждого отдельного числа:0
- 5. Какие еще аксиомы нужны? (повт.)Существование множества всех
- 6. Пределы расширенияСуществует множество всех объектов с данным
- 7. Неравномощность множества и множества всех его подмножествД.Пусть
- 8. Границы математикиДиагональ Рассела – противоречие.Диагональ Кантора –
- 9. Геометрия. Пятый постулатЧерез точку, лежащую вне данной
- 10. Геометрия. Пятый постулатЯнош Бо́йяи (15.12.1802 — 27.01.1860)
- 11. Математика. Программа ГильбертаГипотеза Континуума – не поправимый
- 12. Задачи нашего курсаПостроить систему доказательствПостроить систему аксиом
- 13. Первый из логических языков нашего курса. Последовательность
- 14. Круг в определении«СЕПУЛЬКИ — важный элемент цивилизации ардритов
- 15. Примеры формул:А2, (А1
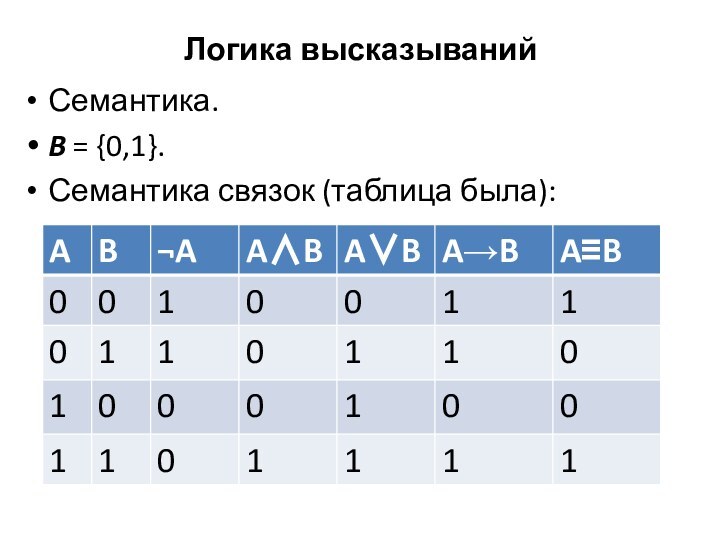
- 16. Логика высказыванийСемантика. B = {0,1}. Семантика связок (таблица была):
- 17. B N - множество бесконечных последовательностей из
- 18. Логика высказываний. СемантикаЗначение формулы при данной интерпретации
- 19. Логика высказываний. СемантикаНахождение значенияЗадача. Почему процесс заканчивается?Задача.
- 20. Булевы функции- Функции Bn B. Формула
- 21. Лишние скобкиЗадача. Придумать разумные правила опускания и восстановления скобок.
- 22. СемантикаТерминология и обозначения для формул Обозначение: ╞
- 23. СемантикаТерминология и обозначения для множеств формул Множество
- 24. Пусть ╞ ( ) и ╞
- 25. ╞ 0 ------------
- 26. Теорема компактностиО. Компактное пространство: Из любого покрытия
- 27. Скачать презентацию
- 28. Похожие презентации
ПланАксиомы теории множеств (повт.)Трудности с полнотойЛогика высказываний. Синтаксис и семантика


























Слайд 2
План
Аксиомы теории множеств (повт.)
Трудности с полнотой
Логика высказываний. Синтаксис
и семантика
Слайд 3
Аксиомы теории множеств (повт.)
Существование множеств
x y
(y∊x)
[Аксиома пустого множества]
uv sw (w
∊ s ≡ (w = u w = v))[Аксиома пары]
Пример: {Ø} – непустое множество.
Существование объединения множества:
⋃{{1,2,4},{4,5},{8,7,{9}}} = {1,2,4,5,8,7,{9}}.
Слайд 4
Один из способов
Построение каждого отдельного числа:
0 –
это Ø
1 – это {0}
2 – это {0,1} =
{0,{0}}……Операция S (x) = x ⋃ {x}
Существование множества всех натуральных чисел –
аксиома.
Задача. Написать аксиому существования
натуральных чисел.
Построение натуральных чисел (повт.)
Слайд 5
Какие еще аксиомы нужны? (повт.)
Существование множества всех подмножеств
данного множества:
usv(w(w ∊ v → w ∊
u) ≡ v ∊ s) [Аксиома степени]Множество всех подмножеств множества u можно отождествлять с Bu.
Что нужно для существования множества действительных чисел?
Что нужно для доказательства свойств («аксиом») действительных чисел?
Слайд 6
Пределы расширения
Существует множество всех объектов с данным свойством
– Аксиома?
Для каждого свойства Ф(x) добавить аксиому:
sv ( v ∊ s ≡ Ф(v ))Можно рассмотреть только свойства, определяемые формулами.
Формула Ф(x):
(x∊x) [Диагональ Рассела]
Задача. Может ли существовать требуемое s ?
Можно добавить:
usv (v ∊ s ≡ (v ∊ u Ф(v ))) [Аксиомы выделения, для каждой Ф]
Слайд 7
Неравномощность множества и множества всех его подмножеств
Д.
Пусть f
– функция, отображающая множество A на множество всех его
подмножеств. Будем писать f (x) = y вместо < x; y > ∊ f .Формула Ф(x) :
y (f (x) = y (x∊y)).
Аксиома выделения дает B ⊂ A:
x (x ∊ B ≡ (x ∊ A y (f (x) = y (x∊y)))).
По предположению f (b) = B для некоторого b ∊ A.
b ∊ B ≡ (b ∊ A y (f (b) = y (b∊y))).
Для этих b, B левая часть эквивалентности истинна, а правая – нет (y должно совпадать с B…).
Противоречие.
Теорема Кантора
Слайд 8
Границы математики
Диагональ Рассела – противоречие.
Диагональ Кантора – теорема.
Множество действительных чисел не равномощно множеству натуральных.
Существует ли бесконечное
множество действительных чисел, не равномощное ни всему множеству действительных чисел, ни множеству натуральных чисел? Кантор считал, что нет (Гипотеза Континуума) – содержание Первой Проблемы Гильберта.
Гедель доказал в 1940 году, что Гипотезу Континуума нельзя опровергнуть: она не приводит к противоречию (если теория множеств без нее – не противоречива).
Пол Коэн (02.04.1934 – 23.03.2007) доказал в 1964 году, что Гипотезу Континуума нельзя доказать, если принять естественную систему аксиом о множествах.
Слайд 9
Геометрия. Пятый постулат
Через точку, лежащую вне данной прямой,
можно провести не более одной прямой, не пересекающейся с
данной.«И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, [в сумме]меньшие двух прямых, то продолженные неограниченно эти прямые встретятся с той стороны, где углы меньше двух прямых.»
Попытки доказательства: привести к противоречию отрицание.
Николай Иванович Лобачевский
(20.11.1792 — 12.02.1856) пришел к убеждению: если к геометрии Евклида добавить утверждение о существовании нескольких прямых, проведенных через одну точку и параллельных данной, то противоречия не возникнет, 1829 г. «О началах геометрии» – «неэвклидова геометрия».
Слайд 10
Геометрия. Пятый постулат
Янош Бо́йяи (15.12.1802 — 27.01.1860) Результат
был опубликован в книге его отца в 1832 году.
Отец Бо́йяи привлек внимание Карла Фридриха Гаусса (30.4.1777 — 23.02.1855) к этой публикации. Гаусс – давно знал!
Доказательство утверждения Лобачевского получено Феликсом Клейном (25.4.1849 - 22.6.1925) в 1871 году.
Принципиально выдвижение и отстаивание гипотезы известным ученым – Лобачевским.
Слайд 11
Математика. Программа Гильберта
Гипотеза Континуума – не поправимый случай,
а неизбежная ситуация
Гедель: полная и не противоречивая математика невозможна.
Слайд 12
Задачи нашего курса
Построить систему доказательств
Построить систему аксиом теории
множеств
Изучить полноту и непротиворечивость для построенной системы или ее
частейБудут рассмотрены произвольные системы доказательства, и еще более общие математические объекты – исчисления
Вычислимость…
В наших рассмотрениях мы (как и других разделах математики) используем неформальную теорию множеств
Слайд 13
Первый из логических языков нашего курса.
Последовательность имен
высказываний
А0, А1, А2,… .
Определение формулы
(логики высказываний). Логические константы 0 и 1 – формулы.
Если А – имя высказывания, то А – формула.
Если Ф, Ψ – формулы, τ – связка: (конъюнкция),
(дизъюнкция), → (импликация), ≡ (эквивалентность), то Ф, (Ф τ Ψ) – формулы.
Индуктивное определение (построение)
«Порочный круг» (цикл в определении – circulus in definiendo) –
определение понятия через его же само?
Логика высказываний
Слайд 14
Круг в определении
«СЕПУЛЬКИ — важный элемент цивилизации ардритов (см.)
с планеты Энтеропия (см.). См. СЕПУЛЬКАРИИ». «СЕПУЛЬКАРИИ — устройства для сепуления
(см.)». «СЕПУЛЕНИЕ — занятие ардритов (см.) с планеты Энтеропия (см.). См. СЕПУЛЬКИ».Лем С. «Звёздные дневники Ийона Тихого. Путешествие четырнадцатое.»
Слайд 15
Примеры формул:
А2, (А1 А0),
А1
((А1 А0) ≡ А1),
Как формула
строилась:А1
А0
(А1 А0)
А1
А1
((А1 А0) ≡ А1)
Задача. Как проверить, является ли слово формулой?
Например, формулы ли: )))А0, ((А1А2)) ?
Синтаксис логики высказываний.
Слайд 17 B N - множество бесконечных последовательностей из 0
и 1.
Пояснение:
Выбор элемента = 0, 1, . .
., i … B N означает фиксацию значений имен высказываний А0, А1,…, Аi,… .Всякий элемент B N – интерпретация.
Фиксируем интерпретацию .
Замечание. Нам удобно задавать значения сразу для всех имен высказываний.
Логика высказываний. Семантика
Слайд 18
Логика высказываний. Семантика
Значение формулы при данной интерпретации
B N .
Вычисление индукцией по построению:
Значением логической
константы является она сама. Значением имени высказывания Ai является i .
Значением:
- формулы () является отрицание значения , т.е.
Зн () = 1- Зн .
- формулы (), где ,,, является результат применения к значениям формул , .
Значение формулы – функция BN B.
Наибольший номер имени высказвания в формуле равен n - 1.
формула задает функцию B n B.
Слайд 19
Логика высказываний. Семантика
Нахождение значения
Задача. Почему процесс заканчивается?
Задача. Почему
результат процесса однозначно определен? (однозначность анализа)
Может ли быть, например:
= (11) = (22)?
Слайд 20
Булевы функции
- Функции Bn B.
Формула
задает функцию Bn B.
Задача. Сколько существует
функций: Bn B ? Задача. Всякую ли функцию можно задать
подходящей формулой?
Слайд 22
Семантика
Терминология и обозначения для формул
Обозначение: ╞
– значение при интерпретации равно 1.
выполнена в (при) интерпретации .Обозначение: ╞ – значение при любой интерпретации
равно 1 ( всегда истинно). Такие называются тавтологиями.
ложные (получающие значение 0) при любой интерпретации
называются противоречиями.
, для которой существует интерпретация, в которой она
истинна, называется выполнимой.
Слайд 23
Семантика
Терминология и обозначения для множеств формул
Множество формул
совместно, если существует интерпретация, при которой все его формулы
истинны.Множество формул противоречиво, если не существует интерпретации, при которой все его формулы истинны.
Пусть Δ – множество формул.
Обозначение: Δ╞ – при всякой интерпретации значение равно 1, если значение всех формул из Δ в той же интерпретации – это 1. следует из Δ.
Слайд 24 Пусть ╞ ( ) и ╞ .
Тогда ╞ .
Всюду вычеркнем (то есть – «при
всех » ) и запишем:╞ , ╞ ( )
-------------------------- – Modus ponens («правило вывода»)
╞
То есть, если в каком-то рассуждении мы получили
и , то можем получить .
Примеры и применения.
Распространенные способы рассуждения
Слайд 25
╞ 0
------------ –
доказательство от противного
╞
╞ – контрапозиция
( ), ( ) ╞ – разбор случаев
( ), ( ) ╞ ( ) – доказательство
эквивалентности
Распространенные способы рассуждения
Слайд 26
Теорема компактности
О. Компактное пространство: Из любого покрытия открытыми
можно выбрать конечное подпокрытие.
Т. Топология: Компактное пространство. Семейство замкнутых
множеств. Если всякое конечное подсемейство имеет непустое пересечение, то и пересечение всех множеств семейства не пусто. Т. Логика. Семейство формул. Если всякое конечное подсемейство выполнимо, то и все семейство выполнимо.
Задача. Доказать Теоремы компактности в топологии (для множеств на прямой, например) и логике.