чисел, в которой невозможно предсказать следующее число, даже зная
все предыдущиеСпособы получения:
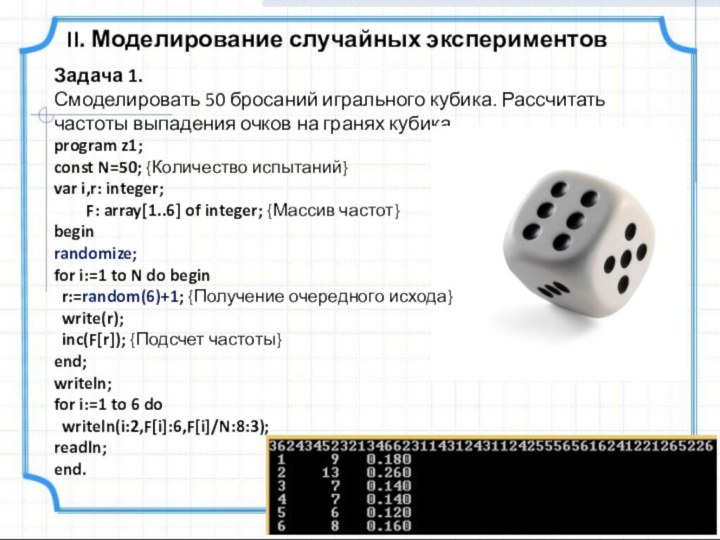
Бросание игрального кубика
Измерение естественного шумового сигнала (радиошум или из космоса)
Выход:
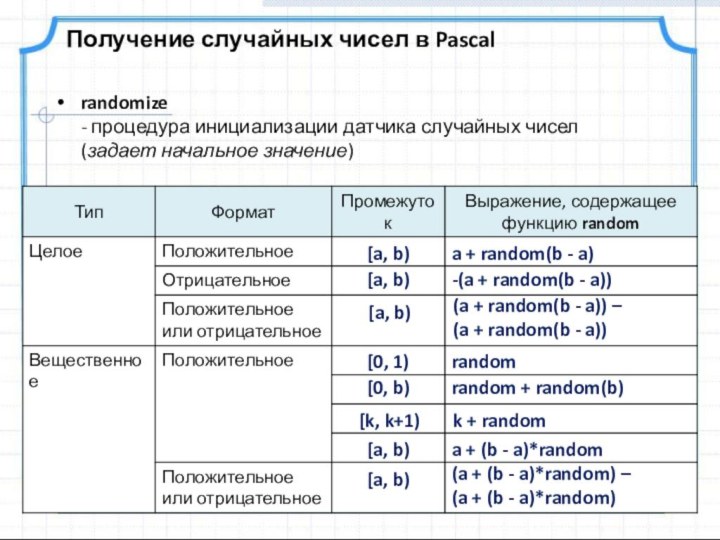
Псевдослучайные числа («как бы случайные») – обладают свойствами случайных чисел, но каждое следующее число вычисляется по заданной формуле.
Алгоритмы получения псевдослучайных чисел
Метод середины квадрата (Дж. фон Нейман, 1946 г.)
Метод середины произведения
Мультипликативный метод (Линейный конгруэнтный генератор,
Д.Г. Лемер, 1949 г.)
Дорогая установка аппаратуры
Невозможность повторения эксперимента





![Презентация по теме Применение Pascal в математической статистике и теории вероятностей Домашнее заданиеЛицей ИГУ г. Иркутска, liguirk.ru*Конспект«19_[ДЗ]Применение Pascal в МС и ТВ.doc»](/img/tmb/6/578195/1412870cb30fc07bcf81b7cad8429713-720x.jpg)