- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Логарифмическая функция
Содержание
- 2. Устная работаВычислиlog981=log416=log0.25=log91=log99=log 0.30.0081=log981=
- 3. Определение. Логарифмом положительного числа b по положительному
- 4. Теорема об обратных функциях Если функция f(x)
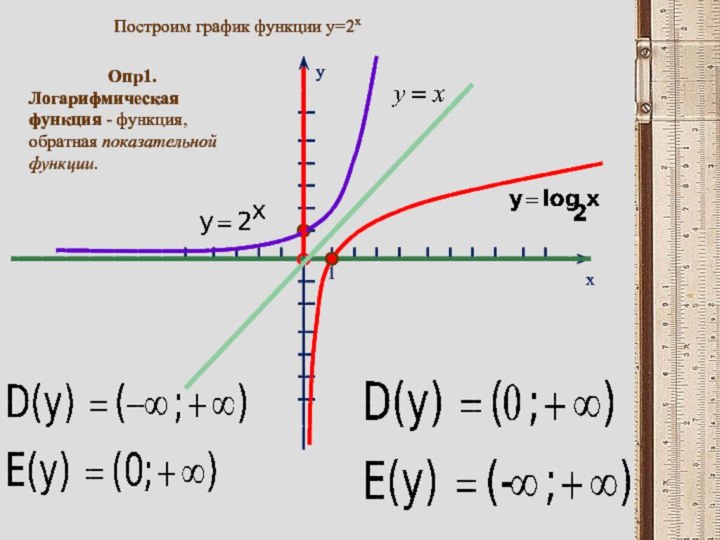
- 5. yx1Построим график функции y=2xОпр1.Логарифмическая функция - функция, обратная показательной функции.
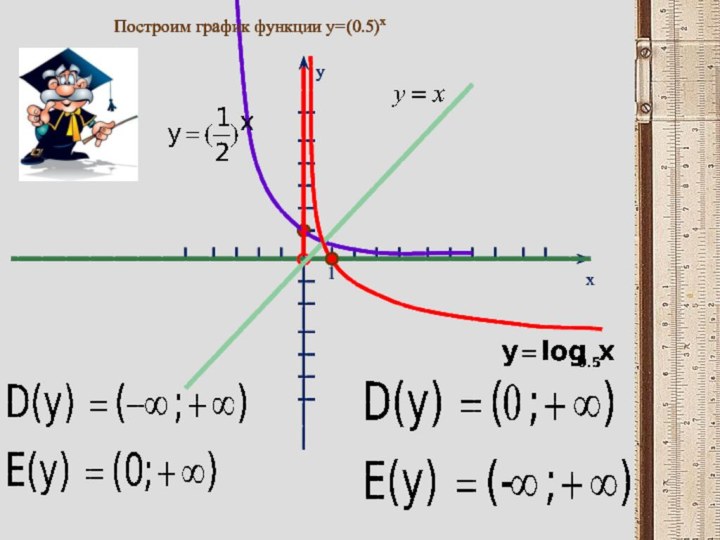
- 6. yx1Построим график функции y=(0.5)x
- 7. Функция вида y = loga х
- 8. Постройте графики функций:
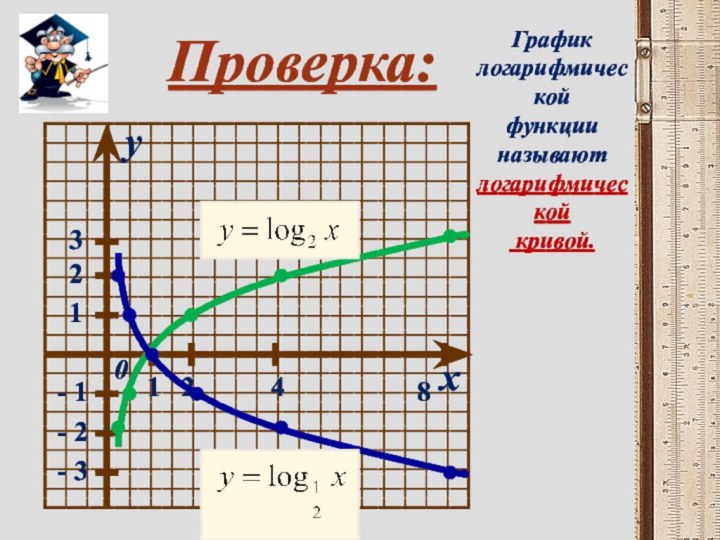
- 9. xy01231248- 1- 2- 3Проверка:График логарифмическойфункции называютлогарифмической кривой.
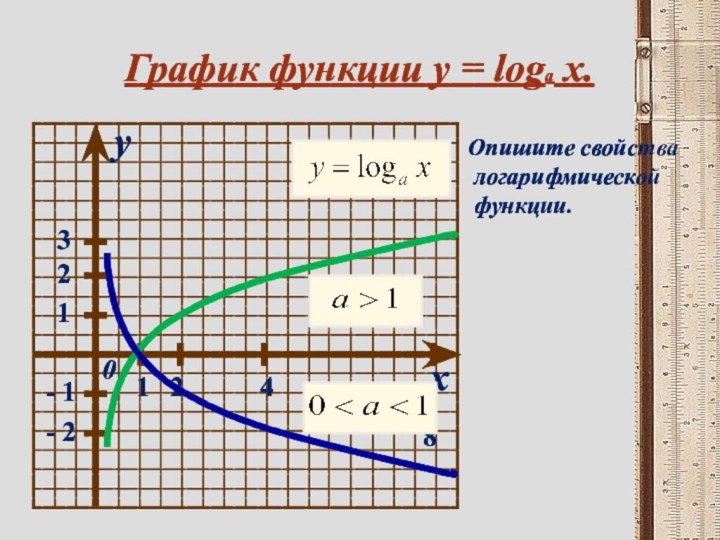
- 10. xy01231248- 1- 2График функции y = loga x.Опишите свойства логарифмической функции.
- 11. 1) D(f) = (0, + ∞);2) не
- 12. 1) D(f) = (0, + ∞);2) не
- 14. Задание №1Найдите наибольшее и наименьшее значения функции
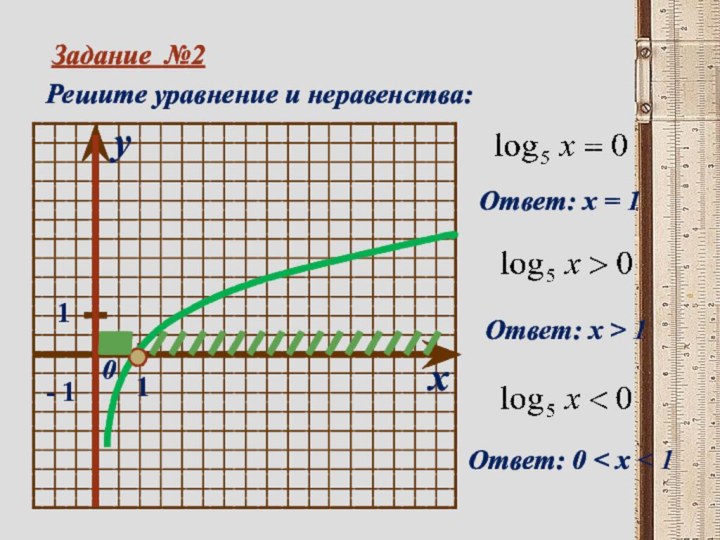
- 15. Задание №2Решите уравнение и неравенства:xy011- 1 Ответ:
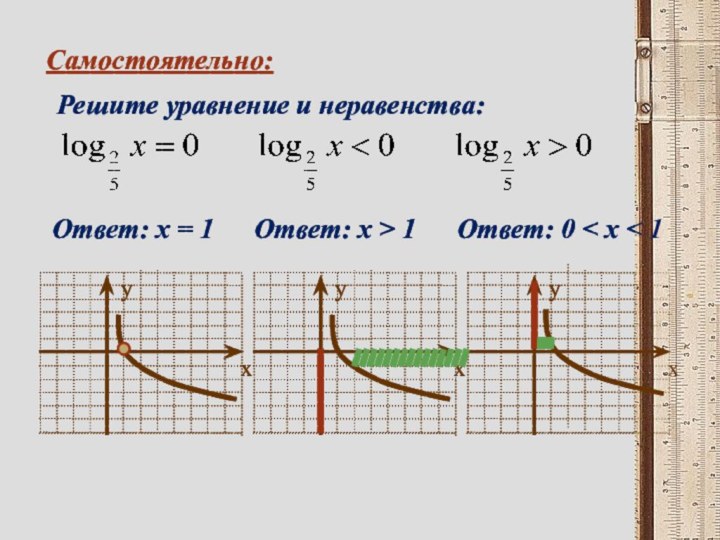
- 16. Самостоятельно:Решите уравнение и неравенства:Ответ: х = 1Ответ: х > 1Ответ: 0 < х < 1
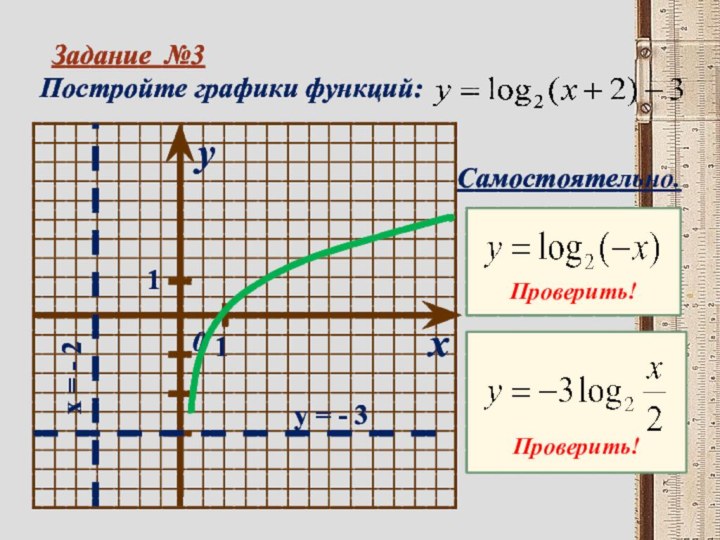
- 17. Задание №3Постройте графики функций:xy011y = - 3 x = - 2Самостоятельно.
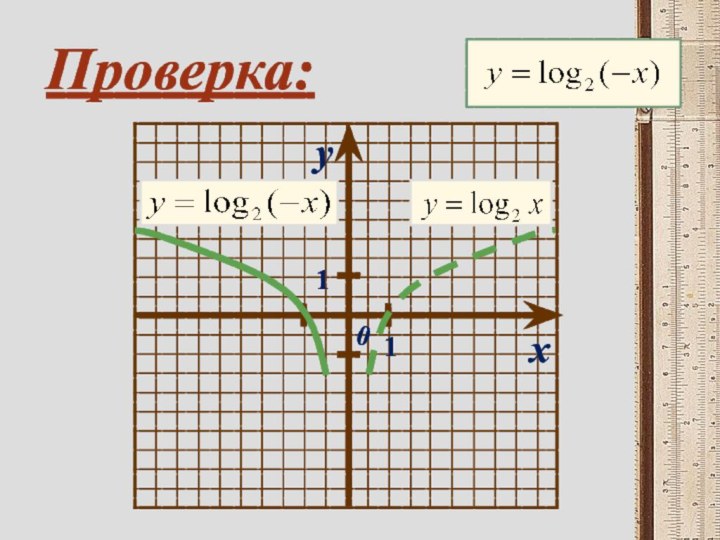
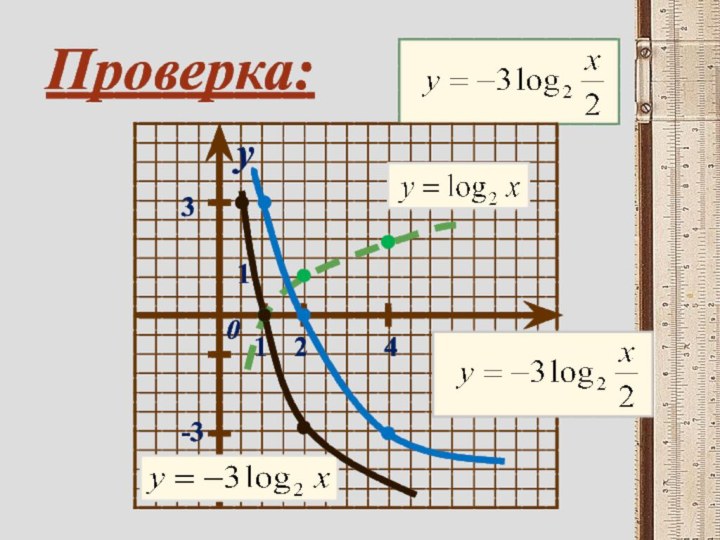
- 18. xy011 Проверка:
- 19. Скачать презентацию
- 20. Похожие презентации
Устная работаВычислиlog981=log416=log0.25=log91=log99=log 0.30.0081=log981=








Слайд 4
Теорема об обратных функциях
Если функция f(x) определена и
монотонна на некотором промежутке X,
причем
D(f)=X,E(f)=Y, то
существует обратная ей функция g(x), определенная на Y, т.е. D(g)=Y
E(g)=X,
причем, монотонность сохраняется. Графики взаимообратных функций симметричны относительно прямой y=x
Слайд 5
y
x
1
Построим график функции y=2x
Опр1.
Логарифмическая функция - функция, обратная
показательной функции.
Слайд 7
Функция вида y = loga х
(где
а > 0, а ≠ 1) называется логарифмической.
D(y):(0;+∞) Это следует из определения логарифма, так как выражение logax имеет смысл только при x > 0.
Слайд 11
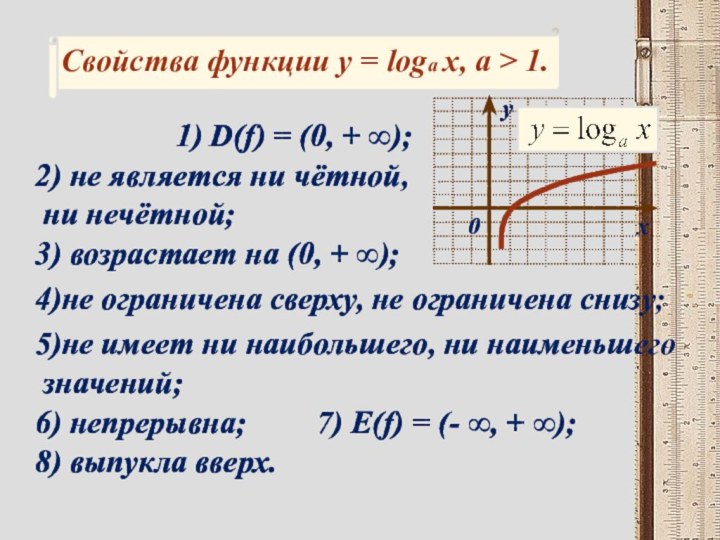
1) D(f) = (0, + ∞);
2) не является
ни чётной,
ни нечётной;
3) возрастает на (0, +
∞); 4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
8) выпукла вверх.
Слайд 12
1) D(f) = (0, + ∞);
2) не является
ни чётной,
ни нечётной;
3) убывает на (0, +
∞); 4)не ограничена сверху, не ограничена снизу;
5)не имеет ни наибольшего, ни наименьшего
значений;
6) непрерывна;
7) E(f) = (- ∞, + ∞);
8) выпукла вниз.
Слайд 14
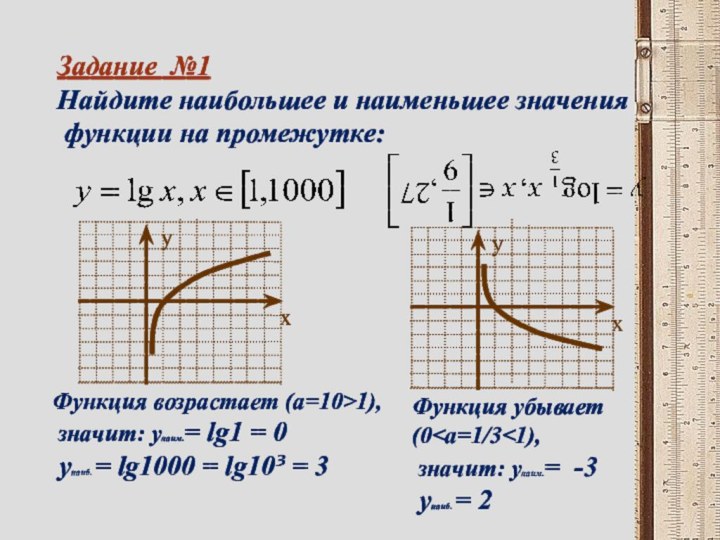
Задание №1
Найдите наибольшее и наименьшее значения
функции на
промежутке:
Функция возрастает (а=10>1),
значит: yнаим.= lg1 = 0
yнаиб.
= lg1000 = lg10³ = 3Функция убывает
(0
yнаиб. = 2





























