Слайд 2
История возникновения чисел
У древних людей, кроме
каменного топора и шкуры вместо одежды, ничего не было,
поэтому считать им было нечего. Постепенно они стали приручать скот, возделывать поля; появилась торговля, и тут уж без счета никак не обойтись.
Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги.
Слайд 3
Древние шумеры.
Первыми придумали запись чисел древние шумеры.
Они пользовались всего двумя цифрами.
Вертикальная черточка обозначала одну
единицу, а угол из двух лежачих черточек – десять.
Эти черточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки.
Слайд 4
Древний народ майя.
Древний народ майя вместо самих
цифр рисовал страшные головы,
как у пришельцев,
и отличить
одну голову – цифру от другой было очень сложно.
Слайд 5
История возникновения чисел
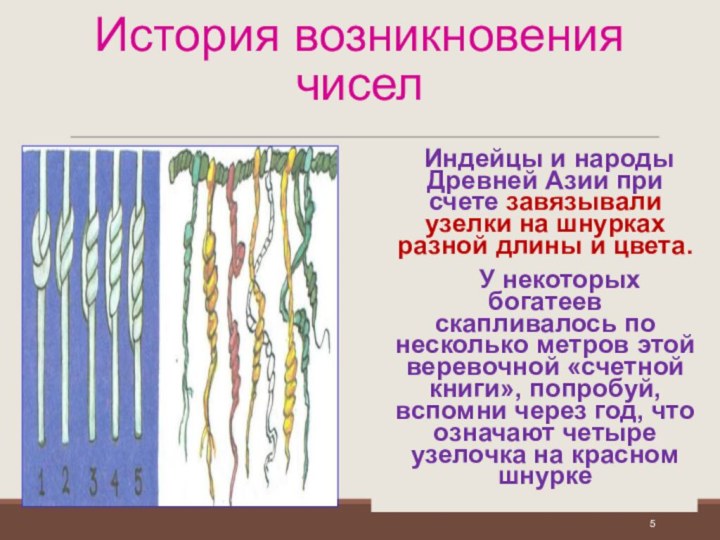
Индейцы и народы Древней Азии
при счете завязывали узелки на шнурках разной длины и
цвета.
У некоторых богатеев скапливалось по несколько метров этой веревочной «счетной книги», попробуй, вспомни через год, что означают четыре узелочка на красном шнурке
Слайд 6
Древние индийцы.
Было очень неудобно хранить глиняные таблички, веревки
с узелками и рулоны папируса.
И это продолжалось
до тех пор, пока древние индийцы не изобрели
для каждой цифры свой знак.
Вот как они выглядели
Слайд 7
Арабские цифры
Арабы были первыми, кто заимствовал цифры у
индийцев, и привез их в Европу. Чуть позже арабы
упростили эти значки, они стали выглядеть вот так.
Они похожи на многие наши цифры. Арабы нуль, или «пусто», называли «сифра». С тех пор и появилось слово «цифра». Правда, сейчас цифрами называются все десять значков для записи чисел, которыми мы пользуемся
Слайд 8
Системы счета
Десятичную систему счисления ввели римляне. Римские
цифры до сих пор используют в часах и для
оглавления книг, но такая система цифр тоже была слишком сложной для счета.
Предки русского народа – славяне - для обозначения чисел употребляли буквы.
Этот способ обозначения цифр называется цифирью.
Слайд 9
Большие числа
Для обозначения больших чисел славяне придумали свой
оригинальный способ:
Десять тысяч – тьма,
десять тем – легион,
десять легионов – леодр,
десять леодров – ворон,
десять воронов – колода.
Такой способ обозначения чисел был очень неудобен.
Поэтому Петр I ввел в России привычные для нас десять цифр, которыми мы пользуемся до сих пор.
Слайд 10
Старинные способы быстрого счета
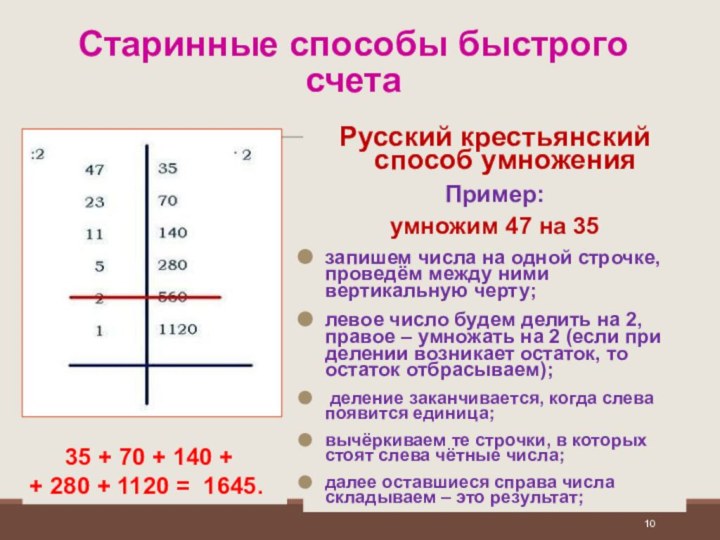
Русский крестьянский способ умножения
Пример:
умножим
47 на 35
запишем числа на одной строчке, проведём между
ними вертикальную черту;
левое число будем делить на 2, правое – умножать на 2 (если при делении возникает остаток, то остаток отбрасываем);
деление заканчивается, когда слева появится единица;
вычёркиваем те строчки, в которых стоят слева чётные числа;
далее оставшиеся справа числа складываем – это результат;
35 + 70 + 140 + + 280 + 1120 = 1645.
Слайд 11
Метод «решетки»
(Абу Абдалах Мухаммед Бен Мусса аль
– Хорезми)
Метод решетки:
Найдем произведение чисел 25 и 63.
Горизонтально
запишем числа 25,
вертикально 63.
Чертим решетку, проводим диагонали.
На пересечениях находим
произведения чисел.
Складываем
числа по диагоналям.
Получили результат: 1575
Слайд 12
Как умножают в Японии?
Так умножают в младших классах
Японии.
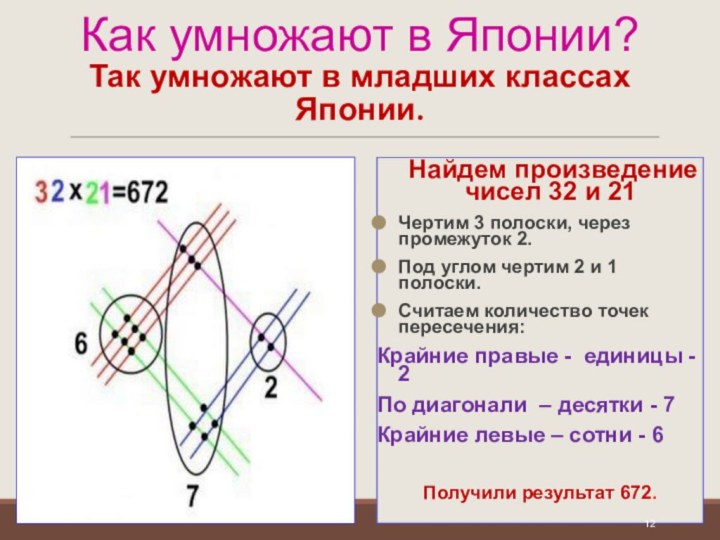
Найдем произведение чисел 32 и 21
Чертим
3 полоски, через промежуток 2.
Под углом чертим 2 и 1 полоски.
Считаем количество точек пересечения:
Крайние правые - единицы - 2
По диагонали – десятки - 7
Крайние левые – сотни - 6
Получили результат 672.
Слайд 13
Система Трахтенберга
Яков Трахтенберг еврейско-русский математик, который, находясь в
заключении в фашистском концлагере во время Второй мировой войны,
разработал систему быстрого счета. Занимался он этим, чтобы сохранить рассудок. Система Трахтенберга позволяет умножать большие числа на небольшие.
Слайд 14
Способ быстрого вычитания
Поразрядное вычитание:
Если число единиц каждого
разряда уменьшаемого больше, то вычитаем поразрядно и результаты складываем.
Пример1:
574-243=(500-200)+(70-40)+(4-3)=300+30+1=331.
Если меньше, то занимаем у высшего разряда:
Пример 2:
647–256=(500-200)+(140-50)+(7-6)=300+90+1=391.
Слайд 15
Умножение чисел от 10 до 20
Чтобы найти произведение
чисел
от 10 до 20 необходимо:
к одному
из чисел надо прибавить количество единиц другого, умножить на 10 и прибавить произведение единиц чисел.
Пример 1: 16∙18 = (16+8) ∙ 10 + 6 ∙ 8 = 288,
Пример 2: 17 ∙ 19 = (17+9) ∙ 10 + 7 ∙ 9 = 323
Слайд 16
Умножение на 11
Чтобы двузначное число, сумма цифр
которого не превышает 10, умножить на 11, надо цифры
этого числа раздвинуть и поставить между ними сумму этих цифр.
Примеры:
72 ∙ 11 = 7 (7 + 2) 2 = 792;
35 ∙ 11 = 3 (3 + 5) 5 = 385.
Чтобы умножить на 11 двузначное число, сумма цифр которого 10 или больше 10, надо мысленно раздвинуть цифры этого числа, поставить между ними сумму этих цифр, а затем к первой цифре прибавить единицу, а вторую и последнюю (третью) оставить без изменения.
Пример:
94 ∙ 11 = 9 (9 + 4) 4 = 9 (13) 4 = (9 + 1) 34 = 1034.
Слайд 17
Умножение на 0,5; 1,5; 2,5; 3,5 …
Чтобы умножить
число на 0,5, надо разделить его на 2:
16 · 0,5 = 16 : 2 = 8
Чтобы умножить число на 1,5, надо к данному числу прибавить его половину:
16·1,5 = 16+8= 10+14=24
Чтобы умножить число на 2,5, надо умножить его на два и прибавить половину числа:
16·2,5 = 16·2 + 8 = 32+8= 40
Чтобы умножить число на 3,5, надо умножить его на 3 и прибавить половину числа:
16·3,5 = 16·3+8=48+8 = 40+16=56
и т.д.
Слайд 18
Способы быстрого деления
Последовательное деление
Если делитель является составным
числом, то разлагаем его на два или большее число
множителей, а потом выполняем последовательное деление:
720:45 = (720:9):5 = 80:5 = 16,
9324:36 = (9324:9):4 = 1036:4 = 259
945:35 = (945:5):7 = 179:7 = 27
Слайд 19
Деление на 0,5; 0,25; 0,125
Чтобы разделить число на
0,5, нужно это число умножить на 2:
32 : 0,5
= 32 · 2 = 60 + 4 = 64
Чтобы разделить число на 0,25, нужно это число умножить на 4:
32 : 0,25 = 32 · 4 = 120 + 8 = 128
Чтобы разделить число на 0,125, нужно это число умножить на 8:
32 : 0,125 = 32 · 8 = 240 + 16 = 256
Слайд 20
Угадывание задуманного числа
Предложите своим друзьям задумать любые числа.
Пусть каждый прибавит к своему задуманному числу 5.
Полученную сумму
пусть умножит на 3.
От произведения пусть отнимет 7.
Из полученного результата пусть вычтет ещё 8.
Листок с окончательным результатом пусть каждый отдаст вам. Глядя на листок, вы тут же говорите каждому, какое число он задумал.
(x+5 ) · 3 - 7- 8 = 3x +15 – 15 = 3x
Чтобы угадать задуманное число, результат, написанный на бумажке или сказанный вам устно, разделить на 3