- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Дәрәҗә. Дәрәҗәләрне тапкырлау һәм бүлү темасы буенча презентация.
Содержание
- 2. 7∙7∙7∙7∙7=7«җиденең бишенче дәрәҗәсе»77 – дәрәҗәнең нигезе5 – дәрәҗәнең күрсәткече
- 3. 7∙7³=(7∙7∙7∙7∙7)∙(7∙7∙7)=7∙7∙7∙7∙7∙7∙7∙7==787∙7=(7∙7∙7∙7∙7)∙7=7∙7∙7∙7∙7∙7==7671=7181=181041=104
- 4. Билгеләмә: Һәркайсы а га нигез булып n
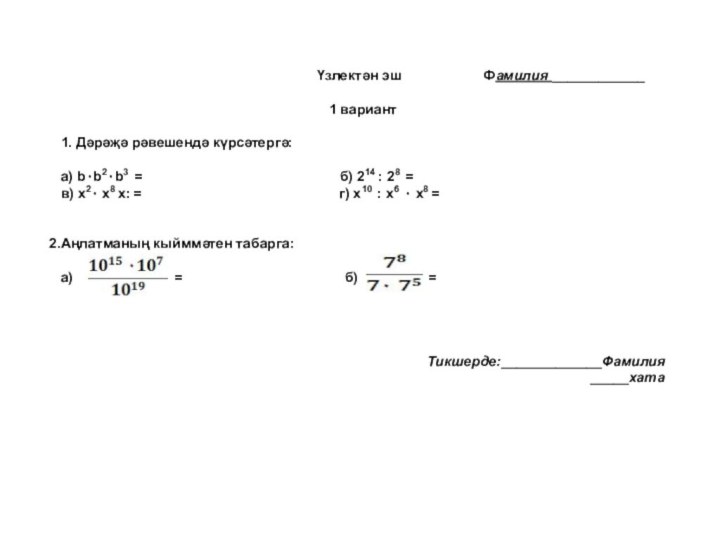
- 5. anнигезекүрсәткечдәрәҗә«a ның n нчы дәрәҗәсе»«n-я степень числа a»
- 6. a2a санының квадраты a3 a санының кубыa
- 7. 11БИРЕМ 2: 6,1 санын , калькулятор кулланып җиденче дәрәҗәгә күтәрик.6,1∙ 6,1∙ 6,1∙ 6,1∙ 6,1∙ 6,1∙ 6,1
- 8. Бирем 3Аңлатманың кыйммәтен исәплик:-62+64:(-2)51) 62=36;2) (-2)5 =-32;3) 64:(-32)=-2;4) -36+(-2)=-38.
- 9. 50=1(-6,3)0=1 00 - АҢЛАТМАСЫНЫҢ МӘГЪНӘСЕ ЮК!0n = 0
- 10. мисал1 -3 санын дүртенче һәм бишенче дәрәҗәгә күтәрик (-3)4=(-3)∙(-3)∙(-3)∙(-3)= 81(-3)5=(-3)∙(-3)∙(-3)∙(-3)∙(-3)=-243
- 11. Нульнең теләсә нинди дәрәҗәсе нульгә тигез;
- 12. a∙a²=(a∙a∙a∙a∙a)∙(a∙a)=a∙a∙a∙a∙a∙a∙a=a7Әгәр a – ирекле сан, ә m
- 13. НИГЕЗЛӘРЕ БЕРТӨРЛЕ БУЛГАН ДӘРӘҖӘЛӘРНЕ ТАПКЫРЛАГАНДА, НИГЕЗЕН ЭЛЕККЕЧӘ КАЛДЫРАЛАР, Ә КҮРСӘТКЕЧЛӘРЕН КУШАЛАР.
- 14. a8:a3a3∙a5=a8=a5Әгәр a – нульгә тигез булмаган теләсә
- 15. НИГЕЗЛӘРЕ БЕРТӨРЛЕ БУЛГАН ДӘРӘҖӘЛӘРНЕ БҮЛГӘНДӘ, НИГЕЗЕН ЭЛЕККЕЧӘ КАЛДЫРАЛАР, Ә БҮЛЕНҮЧЕНЕҢ ДӘРӘҖӘ КҮРСӘТКЕЧЕННӘН БҮЛҮЧЕНЕҢ ДӘРӘҖӘ КҮРСӘТКЕЧЕН АЛАЛАР
- 16. am:am=am-m=a0,монда a≠0am:am=1a0=1,монда a≠0
- 17. Хатаны тап! Аңлатмаларны гадиләштергәндә укучы хата җибәргән:
- 18. Өйрәнгән кагыйдәләрне кулланып, тапкырчыгышны дәрәҗә рәвешендә
- 19. Дөрес исәпләнгән булса торып басырга, ә дөрес
- 20. Дөрес җаваплар:(хаталы эшләр кызыл төс белән төзәтелгән)
- 21. am∙an=am+nam:an=am-n,әгәр a≠0,m һәм n – бөтен тискәре булмаган саннар
- 23. Үзлектән эш
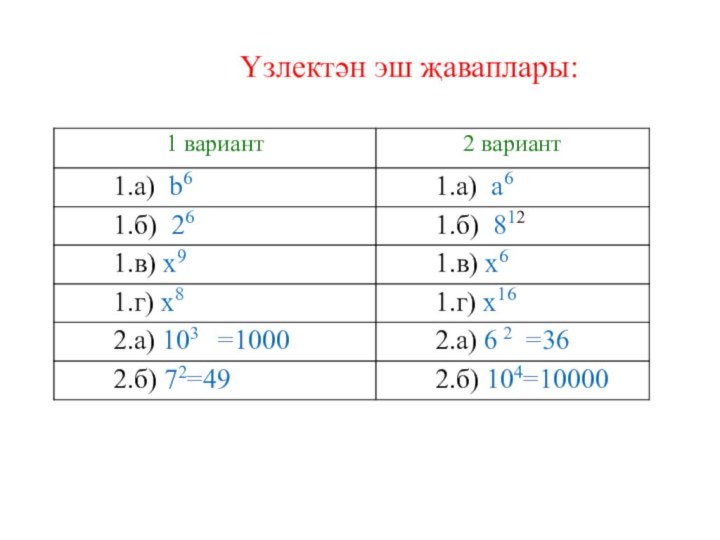
- 24. Үзлектән эш җаваплары:
- 25. Скачать презентацию
- 26. Похожие презентации
7∙7∙7∙7∙7=7«җиденең бишенче дәрәҗәсе»77 – дәрәҗәнең нигезе5 – дәрәҗәнең күрсәткече






















Слайд 3
7∙7³
=(7∙7∙7∙7∙7)∙(7∙7∙7)
=7∙7∙7∙7∙7∙7∙7∙7
=
=78
7∙7
=(7∙7∙7∙7∙7)∙7
=7∙7∙7∙7∙7∙7
=
=76
71=7
181=18
1041=104
Слайд 4 Билгеләмә: Һәркайсы а га нигез булып n тапкырлаучының
тапкырчыгышы а санының 1 дән зуррак натураль n күрсәткечле дәрәҗәсе
дип атала.an = а * а * а *....* а , n > 1
n тапкыр
а саның күрсәткече 1 гә тигез булган дәрәҗәсе дип а саны үзе атала.
a1 = а
Слайд 6
a2
a санының квадраты
a3
a санының кубы
a санының
n-нчы дәрәҗәсен табуны санны n- нчы дәрәҗәгә
күтәрү дип әйтәләр.
Слайд 7
11
БИРЕМ 2:
6,1 санын , калькулятор кулланып җиденче
дәрәҗәгә күтәрик.
6,1∙ 6,1∙ 6,1∙ 6,1∙ 6,1∙ 6,1∙ 6,1
Слайд 8
Бирем 3
Аңлатманың кыйммәтен исәплик:
-62+64:(-2)5
1) 62=36;
2) (-2)5 =-32;
3) 64:(-32)=-2;
4)
-36+(-2)=-38.
Слайд 10
мисал1
-3 санын дүртенче һәм бишенче дәрәҗәгә күтәрик
(-3)4
=(-3)∙(-3)∙(-3)∙(-3)
= 81
(-3)5
=(-3)∙(-3)∙(-3)∙(-3)∙(-3)
=-243
Слайд 11
Нульнең теләсә нинди дәрәҗәсе нульгә тигез;
Уңай
санның теләсә нинди дәрәҗәсе уңай сан була;
Тискәре санның
җөп дәрәҗәсе уңай сан, ә так дәрәҗәсе тискәре сан була.
Слайд 12
a∙a²
=(a∙a∙a∙a∙a)∙(a∙a)
=a∙a∙a∙a∙a∙a∙a
=a7
Әгәр a – ирекле сан, ә m һәм
n – любые теләсә нинди натураль саннар булса, ул
вакытта:am∙an=am+n
am∙an
=(a∙a∙…∙a)∙(a∙a∙…∙a)
=a∙a∙…∙a
=am+n
m тапкыр
n тапкыр
m+n тапкыр
ДӘРӘҖӘНЕҢ ТӨП ҮЗЛЕГЕ
Слайд 13 НИГЕЗЛӘРЕ БЕРТӨРЛЕ БУЛГАН ДӘРӘҖӘЛӘРНЕ ТАПКЫРЛАГАНДА, НИГЕЗЕН ЭЛЕККЕЧӘ КАЛДЫРАЛАР,
Ә КҮРСӘТКЕЧЛӘРЕН КУШАЛАР.
Слайд 14
a8:a3
a3∙a5
=a8
=a5
Әгәр a – нульгә тигез булмаган теләсә нинди
сан, ә m һәм n – ирекле натураль саннар,
һәм m > n, булса:am:an=am-n
Слайд 15 НИГЕЗЛӘРЕ БЕРТӨРЛЕ БУЛГАН ДӘРӘҖӘЛӘРНЕ БҮЛГӘНДӘ, НИГЕЗЕН ЭЛЕККЕЧӘ КАЛДЫРАЛАР,
Ә БҮЛЕНҮЧЕНЕҢ ДӘРӘҖӘ КҮРСӘТКЕЧЕННӘН БҮЛҮЧЕНЕҢ ДӘРӘҖӘ КҮРСӘТКЕЧЕН АЛАЛАР
Слайд 17
Хатаны тап!
Аңлатмаларны гадиләштергәндә укучы хата җибәргән:
а) 5·5·5·5=45
ж) 240:210=250б) 23٠27=410 д) 71=1
в) 230:210=23 е) 20=2
г) 23+27=210 з) 43=12
Укучы нинди кагыйдәләрне һәм үзлекләрне белми?
Слайд 18
Өйрәнгән кагыйдәләрне кулланып, тапкырчыгышны дәрәҗә рәвешендә күрсәт:
а)
75٠74 =
б) (0, 5)3٠(0, 5)6 =в) m . m 2 = г) (х -a)7 . (х -a)10 =
• Өйрәнгән кагыйдәләрне кулланып, өлешне дәрәҗә рәвешендә күрсәт:
а) 610 : 68 = б)
в) (2a)5 : (2a)3 = г) d24: d24 =
Слайд 19
Дөрес исәпләнгән булса торып басырга,
ә дөрес булмаса
урында калырга (һәр мисал аерым тикшерелә):
1) х3 . х4
= х7
2) 109 : 104 =1013
3) х2 . х3 . х5 = х10
4) 32 . 33. 3=355) а13 : а3 = а10 6) 23 :2=22 7) с2 . с . с = с 3 8) 77 : 74 =73
Слайд 20
Дөрес җаваплар:
(хаталы эшләр кызыл төс белән төзәтелгән) 1)
х3 . х4 = х7 2) 109 : 104 =105 3)
х2 . х3 . х5 = х10 4) 32 . 33. 3=365) а13 : а3 = а10 6) 23 : 2=22 7) с2 . с . с = с 4 8) 77 : 74 =7 3
Слайд 22
Үзлектән эш Фамилия ____________
1 вариант
1. Дәрәҗә рәвешендә күрсәтергә:
а) b٠b2٠b3 = б) 214 : 28 =
в) х2٠ х8 х: = г) х10 : х6 ٠ х8 =
Аңлатманың кыйммәтен табарга:
а) = б) =
Тикшерде:_____________Фамилия
_____хата
Слайд 23 Үзлектән эш
Фамилия ____________
2 вариант
1. Дәрәҗә рәвешендә
күрсәтергә:а) ٠а2٠а = б) 214 : 28 =
в) х8٠ х3 : х5 = г) х14 : х3 ٠ х5 =
Аңлатманың кыйммәтен табарга:
а) = б) =
Тикшерде:_____________Фамилия
_____хата