Презентация на тему Формирование умений применять теорему Пифагора в стандартных и нестандартных ситуациях

по данной теме;
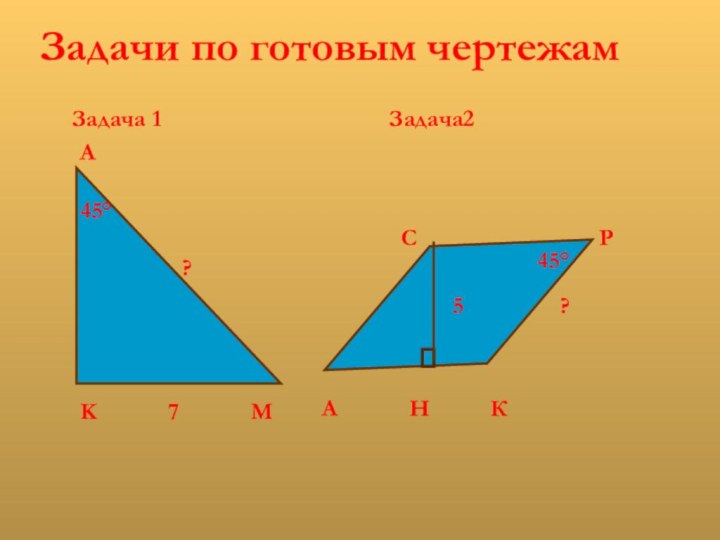
Формирование умений применять теорему Пифагора в стандартных

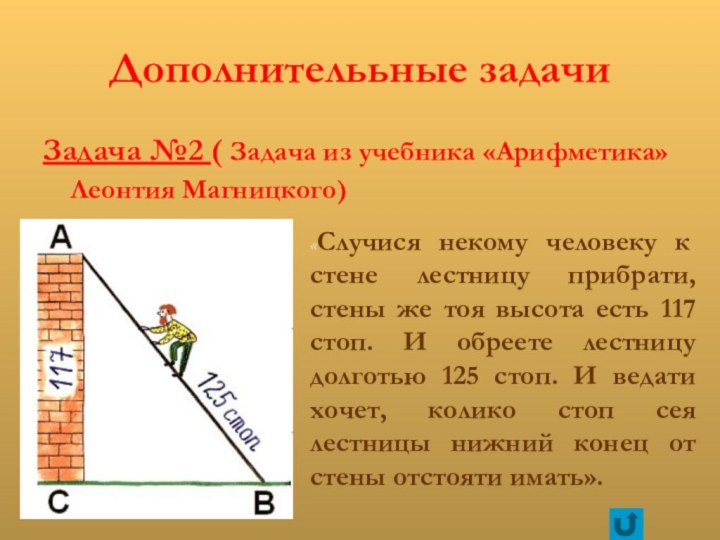
и нестандартных ситуациях;
Знакомство с историей возникновения теоремы
Развитие познавательного интереса у учащихся через решение нестандартных , исторических задач

применять Интернет технологии, создавать компьютерные презентации, проводить отбор необходимого

для урока материала ;
Развитие грамотной математической речи;
Проведение самооценки учебной деятельности
воспитательная:
воспитание настойчивости и трудолюбия

треугольник называется прямоугольным?

Как называются стороны прямоугольного треугольника?
Дайте определение гипотенузы
Дайте определение катета
Сформулируйте теорему Пифагора и теорему, обратную теореме Пифагора

котором один из углов прямой называется прямоугольным

Определение

Гипотенуза это сторона прямоугольного треугольника, лежащая против прямого угла

Катеты это стороны прямого угла в прямоугольном треугольнике

В прямоугольном треугольнике квадрат гипотенузы равен сумме

квадратов катетов а2 + b2 = с2

Обратная теорема Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то этот треугольник прямоугольный

а

b

c

Н К
С
Р
Задача2
45°

Задачи по готовым чертежам

?

5

А

45°

?




K 7 M

Задача 4

Задача5

С Х У М

А В

30°

R

8

N 6 F

L

?

=

=

30°

F

N ? D

G

?

4

4

?

н.э. в Древней Греции на острове Самосе, поэтому его

называют Пифагором Самосским.. По многим свидетельствам, родившийся мальчик был сказочно красив, а вскоре проявил и свои незаурядные способности.

наибольшую славу учёному принесла доказанная им теорема, которая сейчас

носит его имя. Интересна история теоремы Пифагора.. Долгое время считали, что эта теорема до Пифагора не была известна и приписывали ее доказательство Пифагору, поэтому она и носит его имя. Это название сохранилось и поныне. Но оказывается теорема была известна задолго до Пифагора.

работа Вариант 1


Задача 1
О
М
К
13

Задача 2


?
5

10
?
30°
S

L

G

Задача 3

В

А ? D

С

ABCD – ромб,
BD =6; АС = 8

Вариант 2

М F N

L

15

?

_

_

MN=18

В ? К

А

С

3

S L

C G

4

?

О

30°

рос тополь одинокий. Вдруг порыв ветра его ствол надломил.

Бедный тополь упал. И угол прямой с теченьем реки его ствол составлял. Запомни теперь, что в том месте река в четыре лишь фута была широка. Верхушка склонилась у самой реки. Осталось три фута всего от ствола. Прошу тебя скоро теперь мне скажи: « У тополя как велика высота?»

•
-
-
3
Дано:
АМС – прямоугольный
АС =

3 фута
АМ = 4 фута
Найти: АВ
Решение:
1) СМ2 = АМ2 + АС2 (т.Пифагора)
СМ2 = 42 + 32
СМ2 = 16+9
СМ2 = 25
СМ = 5
СВ = СМ = 5 ф (по условию)

2) АВ = АС+СВ = 3 + 5= 8 ф≈[ 1фут ≈ 30,5 см]≈244cм.
Ответ: высота тополя ≈244cм или ≈ 2м44см.

угла использовали бечевку, разделенную узлами на 12 равных частей.

Покажите как они это делали.

●

42

отрезок длиной √2, √3 ?

Высился лотоса цвет.
Он рос одиноко.
И ветер порывом
Отнес

его в сторону.
Нет боле цветка над водой.
Нашел же рыбак его
Ранней весной
В двух футах от места, где рос
Итак: предложу я вопрос:
Как озера вода здесь глубока?

длина лотоса
Т.к. лотос отклонился, то АК = АС
Пусть

АВ=Х- глубина озера
АВС – прямоугольный.
АС2 = СВ2 + АВ2 (т.Пифагора)
(Х+ 0,5)2=22 + Х2
Х2+ Х + 0,25 = 4 +Х2
Х = 3,75
АВ= 3,75(ф)

Ответ: глубина озера 3,75 футов.

его сторон относятся как 3:4. Чему равны длины сторон

экрана? Войдет ли телевизор в нишу стенки, если размеры этой ниши 49см х 35см?

части,
тогда 3х см- длина одной стороны,
4х см

– длина другой стороны.
По теореме Пифагора имеем:
(3х)2 + (4х)2 =2500
25х2 = 2500
х2 = 100
х= 10
3х = 30(см) – длина одной стороны
4х = 40(см) - длина второй стороны
Ответ: размеры телевизора подходят.

главных и, можно сказать , самая главная теорема геометрии.

Ее можно применять
для построения отрезков, длины которых заданы иррациональным числом;
можно строить прямые углы подобно тому, как это делали египтяне при строительстве древних сооружений;
в различных областях человеческой деятельности.

о существовании обитателей Марса подобных человеку.. Было решено передать

обитателям Марса сигнал в виде теоремы Пифагора. Математический факт, выражаемый теоремой Пифагора имеет место всюду и поэтому похожие на нас обитатели другого мира должны понять такой сигнал

1 чжан = 10 чи. В центре его растет

камыш, который выступает над водой на 1 чи. Если потянуть камыш к берегу, то он как раз коснётся его. Спрашивается: какова глубина воды и какова длина камыша?».

Задача № 1 (Задача из китайской «Математики в девяти книгах» )

Леонтия Магницкого)

«Случися некому человеку к стене лестницу прибрати,

стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп. И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать».

стихи.

только мир ее увидит взор, И теорема та, что дал

нам Пифагор, Верна теперь, как в день ее рожденья. За светлый луч с небес вознес благодаренье Мудрец богам не так, как было до тех пор. Ведь целых сто быков послал он под топор, Чтоб их сожгли как жертвоприношенье.
Быки с тех пор, как только весть услышат, Что новой истины уже следы видны, Отчаянно мычат и ужаса полны: Им Пифагор навек внушил тревогу. Не в силах преградить той истине дорогу, Они, закрыв глаза, дрожат и еле дышат. (А. фон Шамиссо, перевод Хованского)

четыре треугольника. А на каждом катете построен квадрат, содержащий

два треугольника. Из рисунка видно, что площадь квадрата, построенного на гипотенузе равна сумме площадей квадратов, построенных на катетах.

Для равнобедренных прямоугольных треугольников