- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по теме: Центральная, осевая симметрия
Содержание
- 2. Симме́трия (др.-греч. соразмерность), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях
- 3. Виды симметрииСимметрия относительно точки (центральная симметрия).Симметрия относительно
- 4. Центральная симметрияЦентральная симметрия - это вид симметрии,
- 5. Центральная симметрияпроизвольный треугольникквадраткругправильный шестиугольникпараллелограммравносторонний треугольникправильный восьмиугольникуголтрапецияромбпрямоугольник
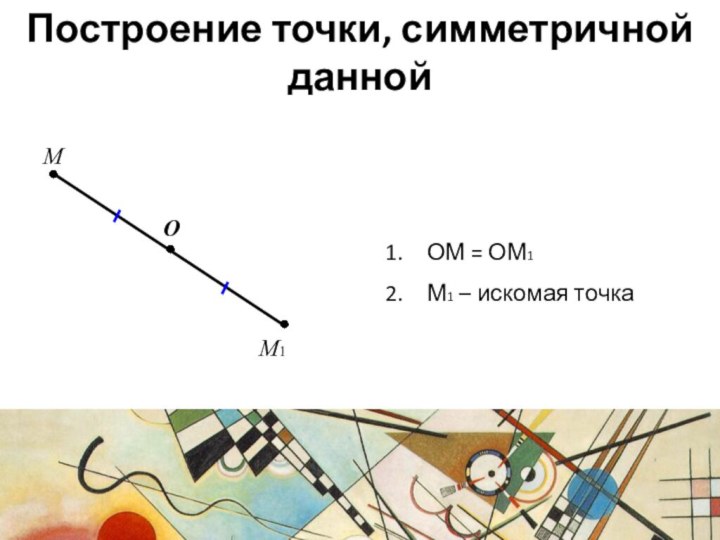
- 6. Построение точки, симметричной данной ОMM1ОМ = ОМ1М1 – искомая точка
- 7. Построение треугольника, симметричного данномуОАА1BB1 CC12. ВО =
- 8. Осевая симметрия Осевая симметрия – это вид симметрии,
- 9. Осевая симметрияпроизвольный треугольникквадраткругправильный шестиугольникпараллелограммравносторонний треугольникправильный восьмиугольникуголтрапецияромбпрямоугольник
- 10. Построение треугольника, симметричного данному относительно осиАА1BB1 CC1 4. А1В1С1 – искомый треугольникаОО1О2
- 11. Симметрия в русском языкеБуквы имеют вертикальную ось
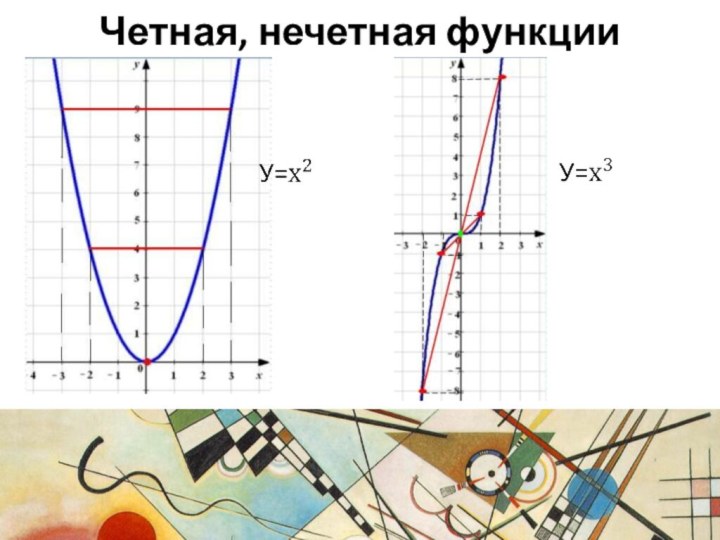
- 12. Четная, нечетная функции
- 13. График четной функция симметричен относительно оси ординат. Четная функция имеет ось симметрии.Четная функция
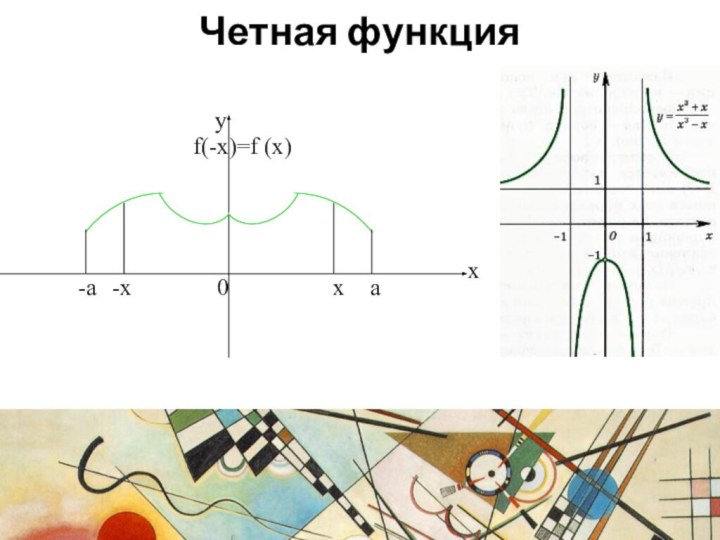
- 14. Четная функция
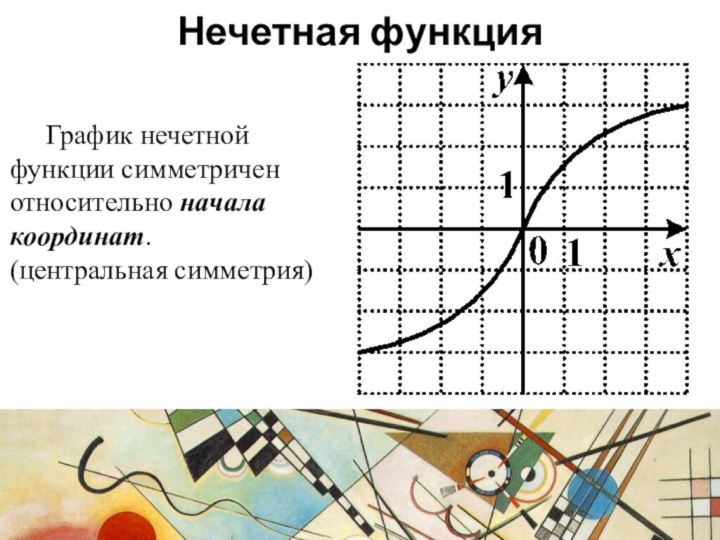
- 15. График нечетной функции симметричен относительно начала координат.(центральная симметрия)Нечетная функция
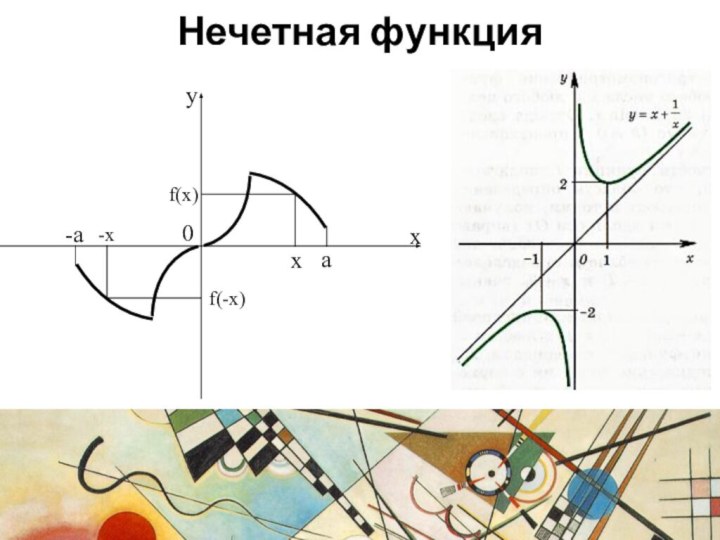
- 16. Нечетная функция
- 17. График четной функция симметричен относительно оси ординат.График нечетной функции симметричен относительно началакоординат.
- 18. ПА РЦИОЛ АКУБФУНКА БЯ
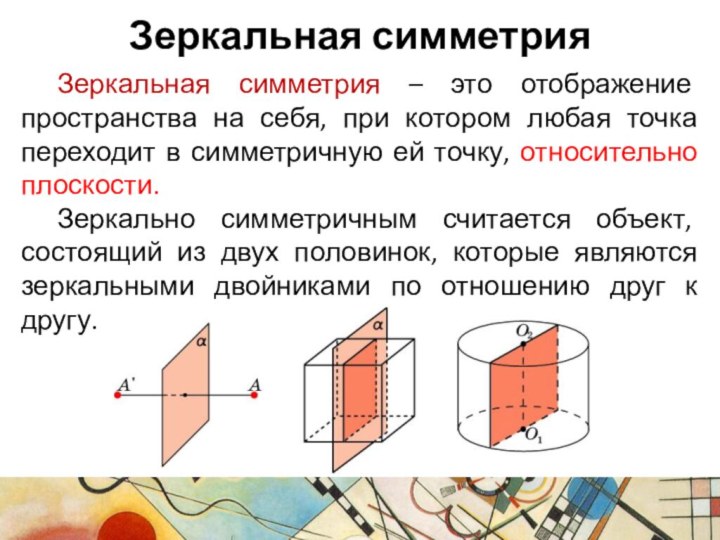
- 19. Зеркальная симметрия Зеркальная симметрия – это отображение пространства
- 20. Зеркальная симметрия
- 21. Зеркальная симметрия
- 22. Зеркальная симметрия
- 23. Переносная симметрияПереносная (скользящая, поступательная) симметрия – это
- 24. Поворотная симметрия Объект обладает поворотной симметрией, если он
- 25. Винтовая или спиральная симметрияВинтовая симметрия - это
- 26. Винтовая или спиральная симметрия Встречаются левые и правые винты .
- 27. Симметрия в архитектуре города Кемерово
- 28. Симметрия в архитектуре города Кемерово
- 29. Симметрия в архитектуре города Кемерово
- 30. Симметрия в архитектуре города Кемерово
- 31. Симметрия в архитектуре города Кемерово
- 32. Симметрия в шорских и телеутских орнаментах
- 33. Симметрия в шорских и телеутских орнаментах
- 34. Симметрия в шорских и телеутских орнаментах
- 35. Симметрия в природе
- 36. Симметрия в природе
- 37. Симметрия в природе
- 38. Симметрия в технике
- 39. Симметрия в технике
- 40. Симметрия в технике
- 41. Симметрия в космосе
- 42. Симметрия в космосе
- 43. Симметрия в космосе
- 44. Симметрия в космосе
- 45. Виды симметрииСимметрия относительно точки (центральная симметрия).Симметрия относительно
- 46. Виды симметрииКакие из следующих букв имеют ось
- 47. Виды симметрииКакие из следующих букв имеют ось
- 48. Скачать презентацию
- 49. Похожие презентации
Симме́трия (др.-греч. соразмерность), в широком смысле — соответствие, неизменность (инвариантность), проявляемые при каких-либо изменениях



































Слайд 2 Симме́трия (др.-греч. соразмерность), в широком смысле — соответствие, неизменность (инвариантность),
проявляемые при каких-либо изменениях
Слайд 3
Виды симметрии
Симметрия относительно точки (центральная симметрия).
Симметрия относительно прямой
(осевая симметрия).
Симметрия относительно плоскости (зеркальная симметрия).
Переносная симметрия.
Поворотная симметрия.
Винтовая симметрия.
Слайд 4
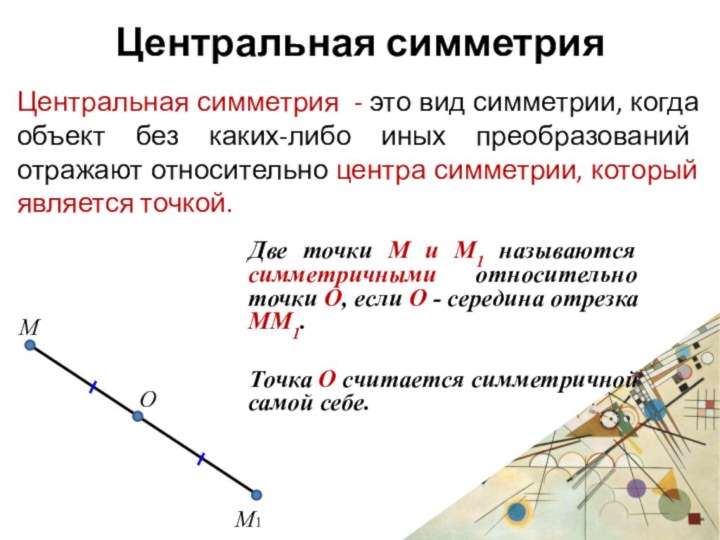
Центральная симметрия
Центральная симметрия - это вид симметрии, когда
объект без каких-либо иных преобразований отражают относительно центра симметрии,
который является точкой.Две точки М и М1 называются симметричными относительно точки О, если О - середина отрезка ММ1.
Точка О считается симметричной самой себе.
Слайд 5
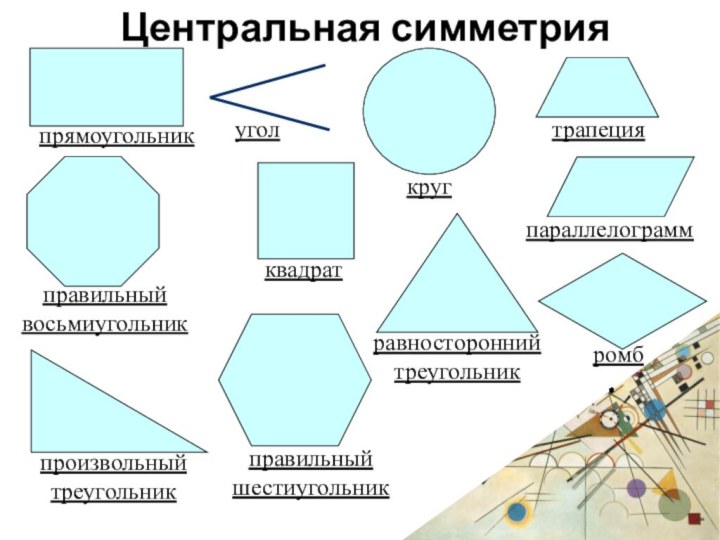
Центральная симметрия
произвольный треугольник
квадрат
круг
правильный шестиугольник
параллелограмм
равносторонний треугольник
правильный восьмиугольник
угол
трапеция
ромб
прямоугольник
Слайд 7
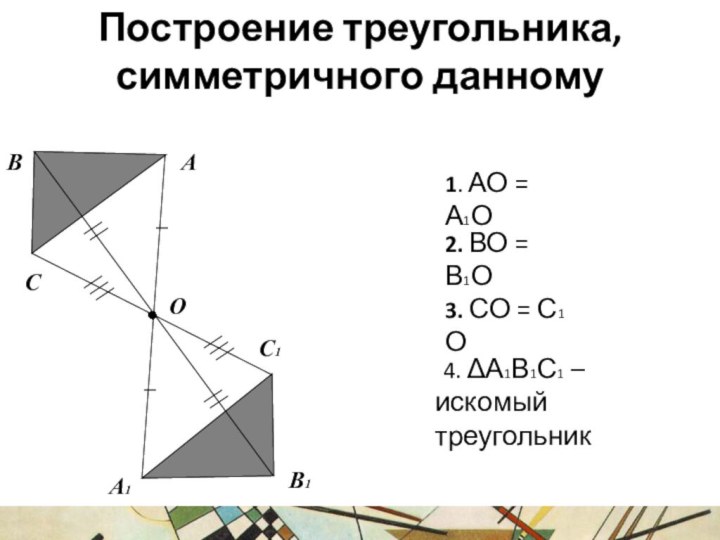
Построение треугольника, симметричного данному
О
А
А1
B
B1
C
C1
2. ВО = В1О
1.
АО = А1О
3. СО = С1 О
4. А1В1С1
– искомый треугольник
Слайд 8
Осевая симметрия
Осевая симметрия – это вид симметрии, когда
объект отражают без каких-либо иных преобразований относительно оси симметрии,
которая является прямой линией.Две точки А и А1 называются симметричными относительно прямой а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
Слайд 9
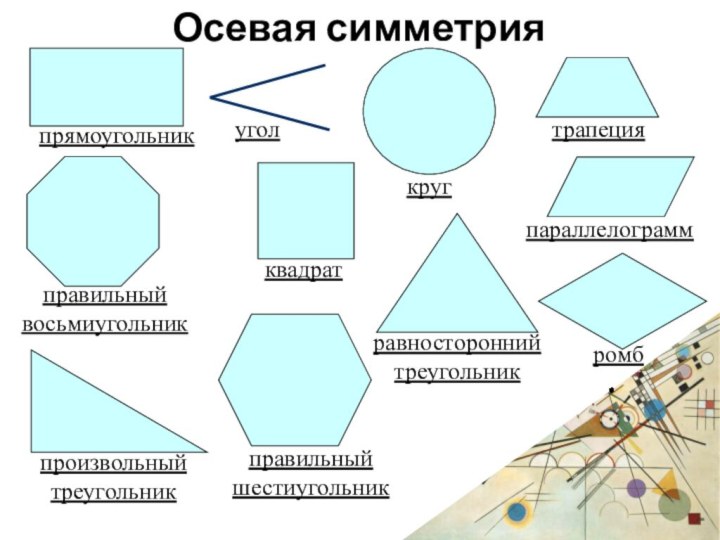
Осевая симметрия
произвольный треугольник
квадрат
круг
правильный шестиугольник
параллелограмм
равносторонний треугольник
правильный восьмиугольник
угол
трапеция
ромб
прямоугольник
Слайд 10
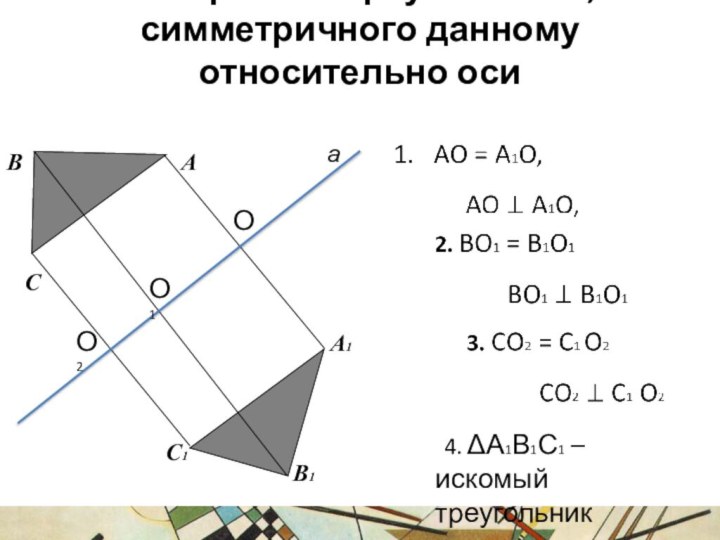
Построение треугольника, симметричного данному относительно оси
А
А1
B
B1
C
C1
4.
А1В1С1 – искомый треугольник
а
О
О1
О2
Слайд 11
Симметрия в русском языке
Буквы имеют вертикальную ось симметрии
Буквы имеют горизонтальную ось симметрии
Буквы имеют по две
оси симметрии А, М, Т, Ш, П
В, З, К, С, Э, Е
Ж, Н, О, Ф, Х
Слайд 13
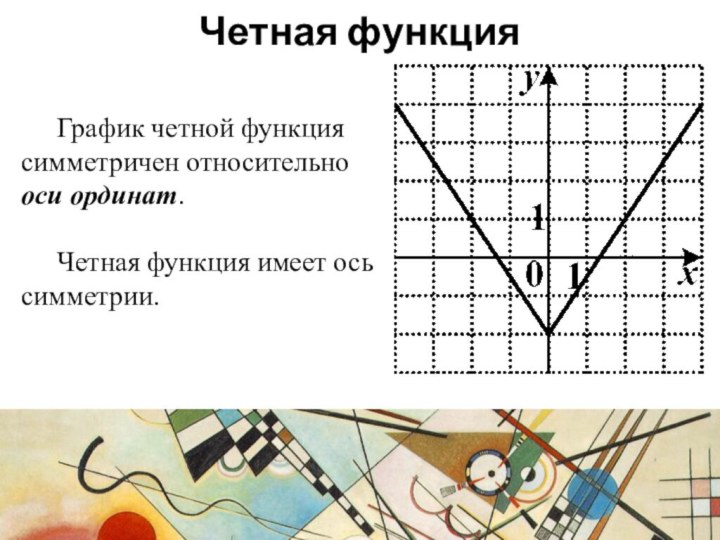
График четной функция симметричен относительно оси ординат.
Четная функция
имеет ось симметрии.
Четная функция
Слайд 15
График нечетной функции симметричен относительно начала координат.
(центральная симметрия)
Нечетная
функция
Слайд 17
График четной функция симметричен относительно оси ординат.
График нечетной
функции симметричен относительно начала
координат.
Слайд 19
Зеркальная симметрия
Зеркальная симметрия – это отображение пространства на
себя, при котором любая точка переходит в симметричную ей
точку, относительно плоскости.Зеркально симметричным считается объект, состоящий из двух половинок, которые являются зеркальными двойниками по отношению друг к другу.
Слайд 23
Переносная симметрия
Переносная (скользящая, поступательная) симметрия – это вид
симметрии, когда объект без каких-либо иных преобразований перемещают куда-либо
вдоль прямой.Примером является орнамент – бордюр.
Слайд 24
Поворотная симметрия
Объект обладает поворотной симметрией, если он совмещается
сам с собой при повороте вокруг некоторой оси на
угол, равный 360/n, где n=2,3,4…. , а указанную ось называют осью поворота n-ого порядка.Поворотную симметрию иначе могут называть радиальной или лучевой симметрией.
Слайд 25
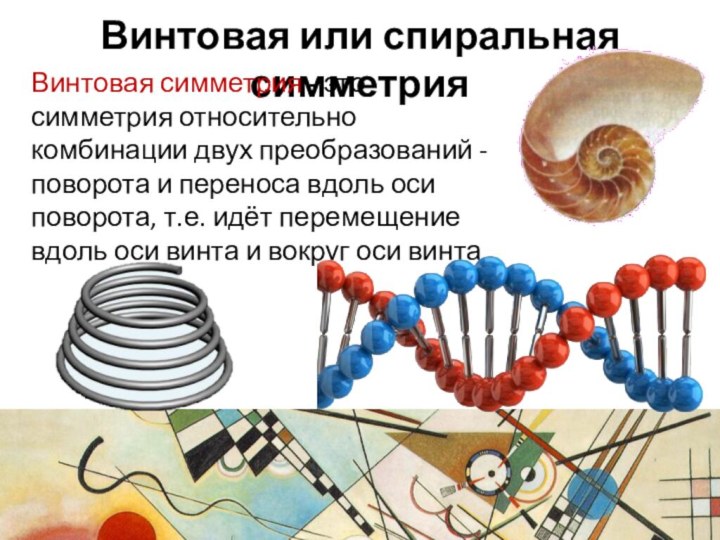
Винтовая или спиральная симметрия
Винтовая симметрия - это симметрия
относительно комбинации двух преобразований - поворота и переноса вдоль
оси поворота, т.е. идёт перемещение вдоль оси винта и вокруг оси винта.
Слайд 45
Виды симметрии
Симметрия относительно точки (центральная симметрия).
Симметрия относительно прямой
(осевая симметрия).
Симметрия относительно плоскости (зеркальная симметрия).
Переносная симметрия.
Поворотная симметрия.
Винтовая симметрия.
Слайд 46
Виды симметрии
Какие из следующих букв имеют ось симметрии:
А, Б, Г, Е, О, F?
Какие из следующих
букв имеют центр симметрии: А, Б, Е, О, F, Х, К, Ж?Какие из следующих фигур имеют ось симметрии: отрезок, квадрат, трапеция?
Какие из следующих фигур имеют центр симметрии: отрезок, квадрат, трапеция?
Слайд 47
Виды симметрии
Какие из следующих букв имеют ось симметрии:
А, Б, Г, Е, О, F?
Какие из следующих
букв имеют центр симметрии: А, Б, Е, О, F, Х, К, Ж?Какие из следующих фигур имеют ось симметрии: отрезок, квадрат, трапеция?
Какие из следующих фигур имеют центр симметрии: отрезок, квадрат, трапеция?





























