- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Из истории развития чисел
Содержание
- 2. Почему возникла необходимость в числах?ОСНОВОПОЛАГАЮЩИЙ ВОПРОС
- 3. Узнать, как развивалось понятие «число» в разные исторические периодыЦЕЛЬ
- 4. Я думаю, что необходимость в числах возникла прежде всего из практических нужд человека.Гипотеза
- 5. Число́ — абстракция, используемая для количественной характеристики объектов
- 6. ВЫВОД: Пока не произошел переход от простого собирания
- 7. Названия чисел у разных народовАвстралийское племена 1
- 8. Перуанские инки вели счет животных и урожая,
- 9. ДРЕВНИЙ ЕГИПЕТЧисло 345 древние египтяне записывали так
- 10. Древний ВавилонЧисла в этой системе счисления составлялись
- 11. Первыми придумали запись чисел древние шумеры. Они
- 12. РИМСКАЯ СИСТЕМА Знакомая нам римская система не слишком
- 13. Славянская система Данная система счисления является алфавитной т.е.
- 14. Древние индийцы изобрели для каждой цифры свой знак. Вот как они выглядели
- 15. Искусство счета развивалось с развитием человечества. Способов
- 16. В основе любого измерения всегда лежит какая-то
- 17. ДРОБИ В РАЗНЫХ ГОСУДАРСТВАХ ДРЕВНОСТИ Вот как
- 18. В китайской «Математике в девяти разделах» уже
- 19. Обходиться только натуральными числами неудобно. Например, ими
- 20. Положительные числа в китайской математике называли «чен»,
- 21. Натуральные числа, противоположные им (отрицательные) числа и
- 22. Еще в Древнем Египте и Вавилоне ХХ
- 23. Еще более странными, чем иррациональные, оказались числа
- 24. Натуральные числа Целые числа Рациональные числа Действительные числа Комплексные числа
- 25. Мы узнали о существовании таких чисел:Векторные (трехмерные
- 26. ВЫВОДЧисло – одно из основных понятий математики;
- 27. 2. Интуитивное представление о числе появилось еще
- 28. ВЫВОД6. В ходе изучения истории развития числа
- 29. Скачать презентацию
- 30. Похожие презентации

























Слайд 4 Я думаю, что необходимость в числах возникла прежде
всего из практических нужд человека.
Гипотеза
Слайд 6
ВЫВОД:
Пока не произошел переход от простого собирания пищи
к активному ее производству, от охоты и рыболовства к
земледелию, люди мало продвинулись в понимании числовых величин Первоначальные представления о числе появились в эпоху каменного века, примерно 100 веков до нашей эры. Древнему человеку хватило того, что он придумал числа «один» и «два». Остальные количества для него оставались неопределенными и объединялись в понятие «много»
Как все это было?
Слайд 7
Названия чисел у разных народов
Австралийское племена
1 –
энэа, 2- петчевал, 3 петчевал-энэа, 4 – петчевал-петчевал…
1 –
мал, 2- булан, 3 –гулиба, 4 –булан-булан…На берегах Амазонки обнаружено племя, которое знало только три числа – 1,2,3, причем число 3 называлось «поэттаррароринкоароак»
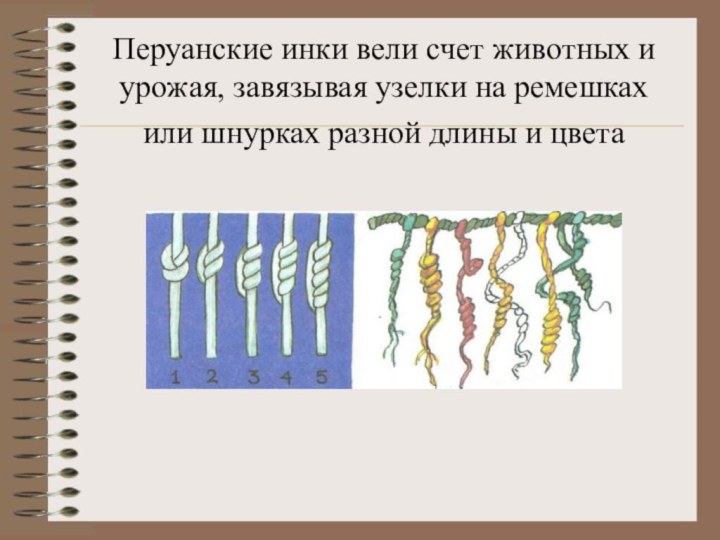
Слайд 8 Перуанские инки вели счет животных и урожая, завязывая
узелки на ремешках или шнурках разной длины и цвета
Слайд 10
Древний Вавилон
Числа в этой системе счисления составлялись из
знаков двух видов: прямой клин служил для обозначения единиц,
а лежачий клин - для обозначения десятков.Например: Число 32 записывали так:
Слайд 11 Первыми придумали запись чисел древние шумеры. Они пользовались
всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а
угол из двух лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом сушили и обжигали. Вот так выглядели эти дощечки
Слайд 12
РИМСКАЯ СИСТЕМА
Знакомая нам римская система не слишком принципиально
отличается от египетской. В ней для обозначения чисел 1,
5, 10, 50, 100, и 1000 используются заглавные латинские буквы I, V, X, C, D и M соответственно, являющиеся цифрами этой системы счисления.Пример 2. Число 444, имеющее в своей десятичной записи 3 одинаковые цифры, в римской системе счисления будет записано в виде CDXLIV=(D-C)+(L-X)+(V-I)=400+40+4
Слайд 13
Славянская система
Данная система счисления является алфавитной т.е. вместо
цифр используются буквы алфавита. Данная система счисления применялась нашими
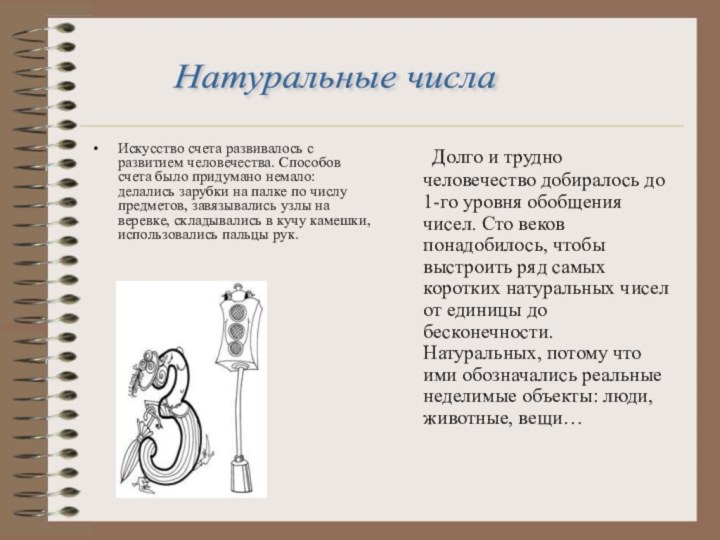
предками и была достаточно сложной, т.к. использует в качестве цифр 27 букв.Слайд 15 Искусство счета развивалось с развитием человечества. Способов счета
было придумано немало: делались зарубки на палке по числу
предметов, завязывались узлы на веревке, складывались в кучу камешки, использовались пальцы рук. Долго и трудно человечество добиралось до 1-го уровня обобщения чисел. Сто веков понадобилось, чтобы выстроить ряд самых коротких натуральных чисел от единицы до бесконечности. Натуральных, потому что ими обозначались реальные неделимые объекты: люди, животные, вещи…
Натуральные числа
Слайд 16 В основе любого измерения всегда лежит какая-то величина.
Потребность в более точных измерениях привела к тому, что
начальные единицы начали дробить на 2, 3 и более частей. Так возникали первые конкретные дроби как определенные части каких-то определенных мерИсторически дроби возникли в процессе измерения
Возникновение дробных чисел
Слайд 17
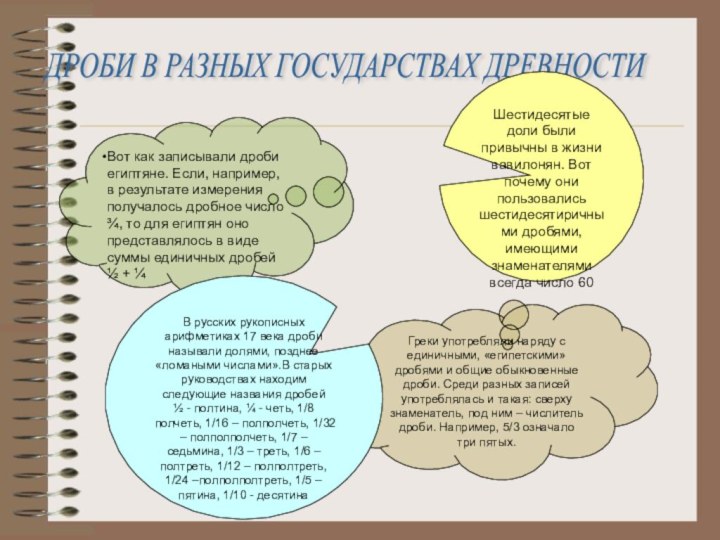
ДРОБИ В РАЗНЫХ ГОСУДАРСТВАХ ДРЕВНОСТИ
Вот как записывали
дроби египтяне. Если, например, в результате измерения получалось дробное
число ¾, то для египтян оно представлялось в виде суммы единичных дробей ½ + ¼Шестидесятые доли были привычны в жизни вавилонян. Вот почему они пользовались шестидесятиричными дробями, имеющими знаменателями всегда число 60
Греки употребляли наряду с единичными, «египетскими» дробями и общие обыкновенные дроби. Среди разных записей употреблялась и такая: сверху знаменатель, под ним – числитель дроби. Например, 5/3 означало три пятых.
В русских рукописных арифметиках 17 века дроби называли долями, позднее «ломаными числами».В старых руководствах находим следующие названия дробей
½ - полтина, ¼ - четь, 1/8 полчеть, 1/16 – полполчеть, 1/32 – полполполчеть, 1/7 –седьмина, 1/3 – треть, 1/6 – полтреть, 1/12 – полполтреть, 1/24 –полполполтреть, 1/5 –пятина, 1/10 - десятина
Слайд 18 В китайской «Математике в девяти разделах» уже имеют
место сокращения дробей и все действия над ними
У
индийского математика Брахмагупты мы находим достаточно развитую систему дробей. У него встречаются разные дроби: и основные, и производные с любым числителем. Числитель и знаменатель записываются так же, как и у нас сейчас, но без горизонтальной чертыАрабы первыми начали отделять чертой числитель от знаменателя
ДРОБИ В РАЗНЫХ ГОСУДАРСТВАХ ДРЕВНОСТИ
Слайд 19 Обходиться только натуральными числами неудобно. Например, ими нельзя
вычесть большее из меньшего. Для такого случая были введены
отрицательные числа:Китайцами – в Х веке до н.э.
Индийцами – в VII веке
Европейцами – только в XIII веке
КОЕ-ЧТО ОБ ОТРИЦАТЕЛЬНЫХ ЧИСЛАХ
Слайд 20 Положительные числа в китайской математике называли «чен», отрицательные
– «фу», их изображали разными цветами: «чен» - красным,
«фу» - черным. Такой способ изображения использовался в Китае до середины 12 столетия., пока Ли Е не предложил более удобное обозначение отрицательных чисел – цифры, которые изображали отрицательные числа, перечеркивали черточкой наискосок справа налевоСлайд 21 Натуральные числа, противоположные им (отрицательные) числа и ноль
называются целыми числами
Целые и дробные числа – рациональные числа
ВЫВОД
С
помощью рациональных чисел можно осуществлять различные измерения с любой точностью. То есть совокупность рациональных чисел достаточна для удовлетворения большинства практических потребностейРациональные числа
Слайд 22 Еще в Древнем Египте и Вавилоне ХХ веков
назад были известны так называемые несоизмеримые отрезки,
которые нельзя было выразить рациональными числамиВЫВОД
РАЦИОНАЛЬНЫЕ И ИРРАЦИОНАЛЬНЫЕ ЧИСЛА образовали ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА
Индийцы рассматривали иррациональные числа как числа нового вида, но допускающие над ними такие же арифметические действия, как и над рациональными числами
В Европе существование геометрических несоизмеримых величин в средние века оспаривалось, но для многих иррациональные числа были лишь символами, лишенными точно определенного содержания, поэтому их называли «глухими», «недействительными», «фиктивными»
ИРРАЦИОНАЛЬНЫЕ ЧИСЛА
Слайд 23 Еще более странными, чем иррациональные, оказались числа новой
природы, их называли «чисто отрицательные», «софистически отрицательными
Долгое время эти
числа считали невозможными, несуществующими, воображаемыми. Декарт назвал их мнимыми, Лейбниц – «уродом из мира идей, сущностью, находящейся между бытием и небытием»Мнимым числам не было места на координатной оси
Долгое время даже математики считали комплексные числа загадочными и пользовались ими только для математических манипуляций (вычислений интегралов, выражать решения дифференциальных уравнений)
Геометрическое истолкование комплексных чисел позволило определить многие понятия, связанные с функцией комплексного переменного
КОМПЛЕКСНЫЕ ЧИСЛА
Слайд 25
Мы узнали о существовании таких чисел:
Векторные (трехмерные числа)
Матричные
(многоэлементные объекты)
Трансфинитные (бесконечные, запредельные числа)
Какие числа следуют за комплексными?
Слайд 26
ВЫВОД
Число – одно из основных понятий математики; зародилось
в глубокой древности и постепенно расширялось и обобщалось.
Задачи измерения
длин, площадей и т.д. привели к понятию рационального (дробного числа)Понятие отрицательного числа возникло у индийцев в 6-11 веках
Потребность в точном выражении отношений величин привела к введению иррациональных чисел.
Рациональные и иррациональные числа составляют совокупность действительных чисел.
В связи с решением квадратных и кубических уравнений в 16 веке были введены комплексные числа.
Слайд 27 2. Интуитивное представление о числе появилось еще у
первобытных людей. Сначала был устный счет предметов без записи
числами.3. Числа появились не сразу. Они появились в первых государствах, а не в племенах и общинах у первобытных людей.
4. Числа появились не в одном месте. В каждом народе придумывали свои обозначения чисел.
5. Числа бывают египетские, вавилонские, греческие, римские, арабские, древнееврейские и т.д. В современном мире используются в основном арабские и немного (чаще в датах) римские цифры.
ВЫВОД
Слайд 28
ВЫВОД
6. В ходе изучения истории развития числа можно
сказать, что числа возникли из практических нужд человека
7. Современная наука
встречается с величинами такой сложной природы, что для их изучения приходится изобретать все новые и новые виды чисел8. К настоящему времени существует семь общепринятых уровней обобщения чисел:
Натуральные
Рациональные
Действительные
Комплексные
Векторные
Матричные
Трансфинитные