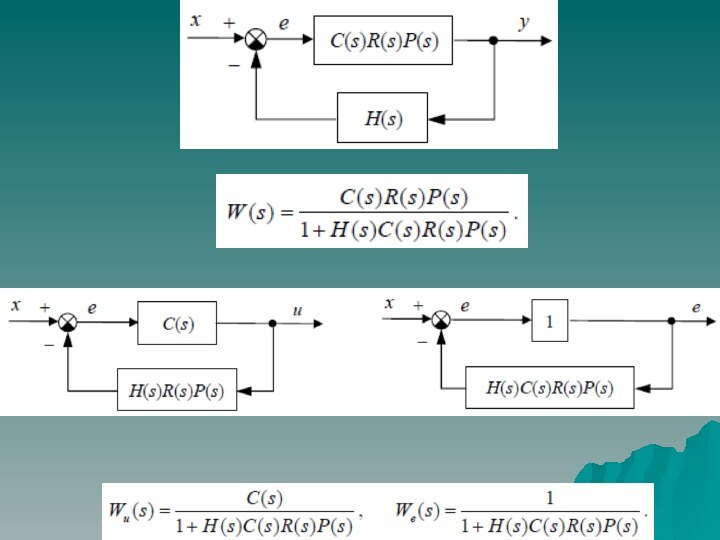
выходной и входной величин при нулевых начальных условиях.
Математическое
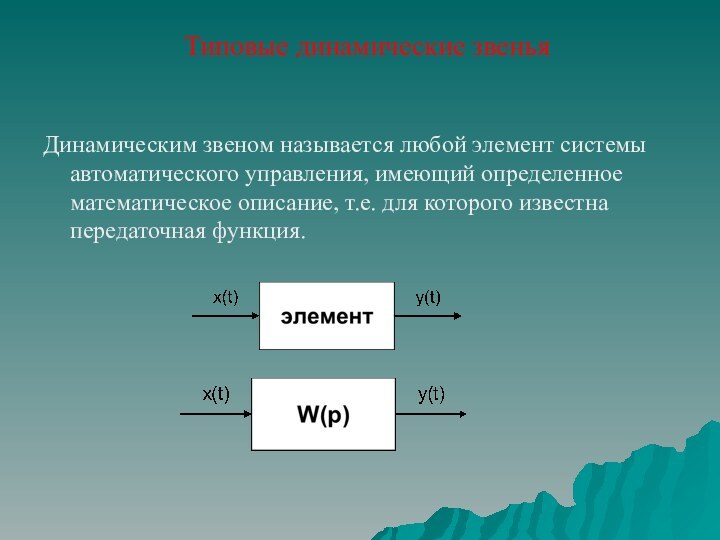
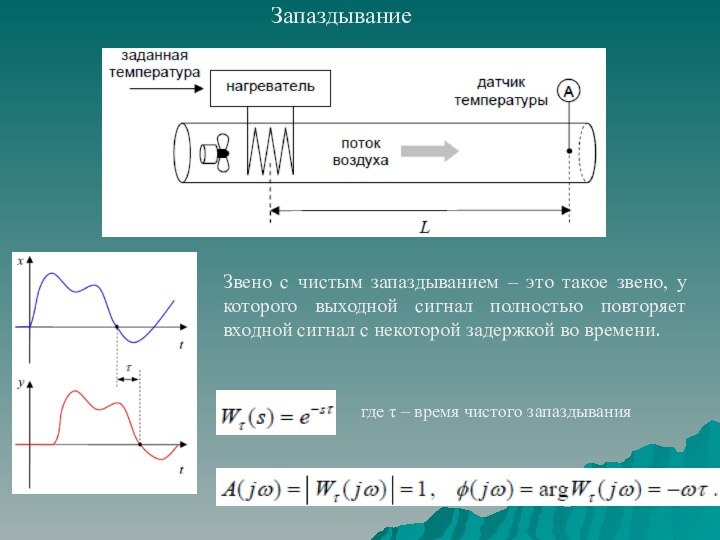
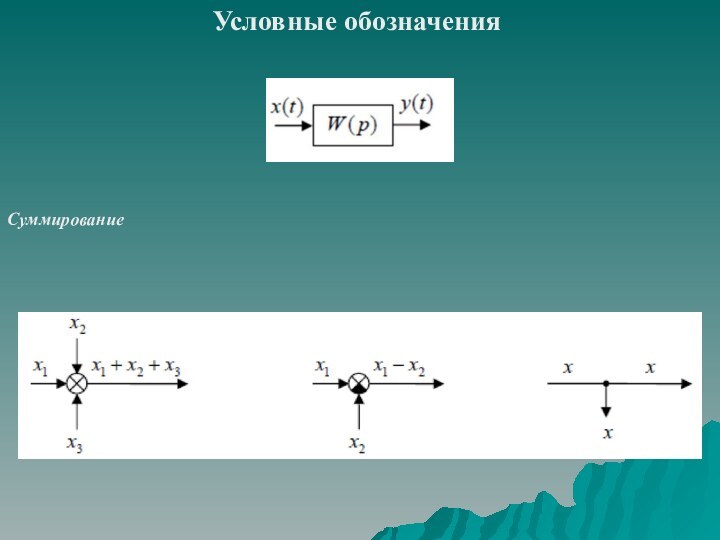
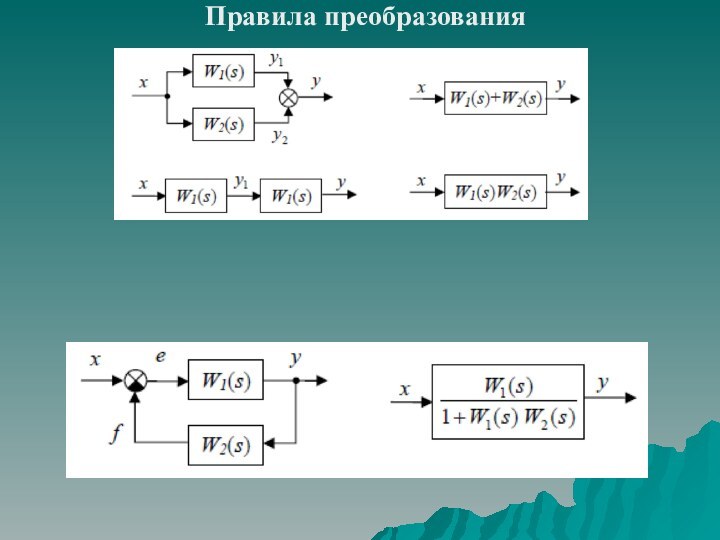
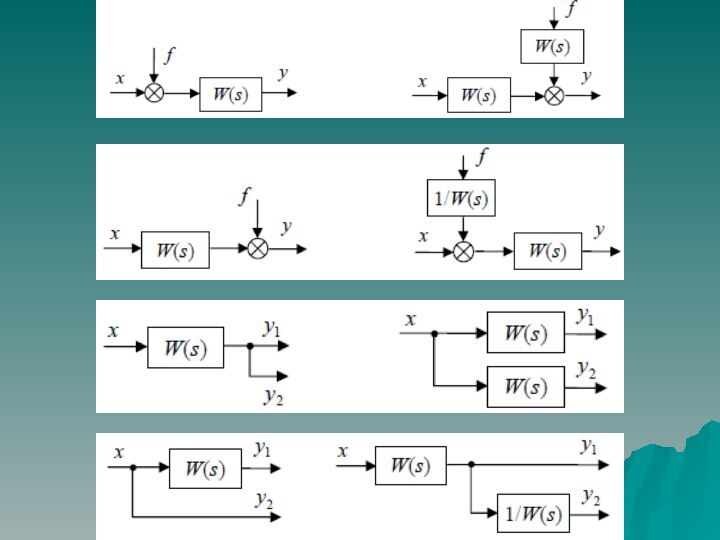
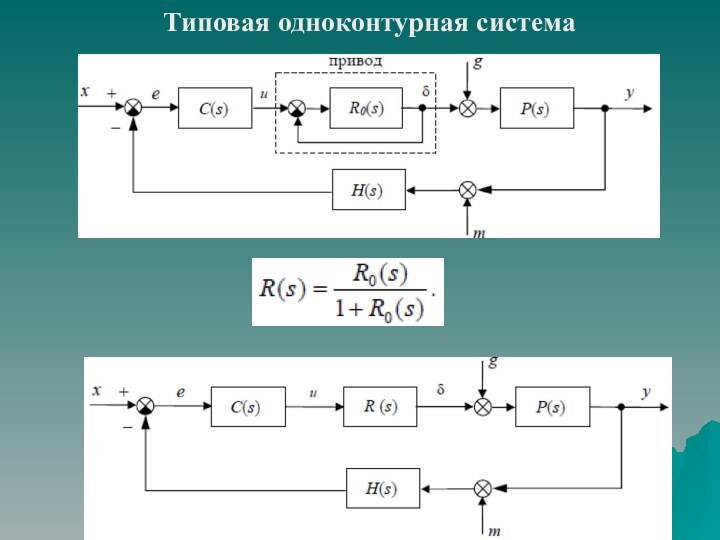
описание линейного непрерывного динамического элемента системы сводится к описанию связи между его входом и выходом. Данная связь может быть задана в виде: линейного дифференциального уравнения;
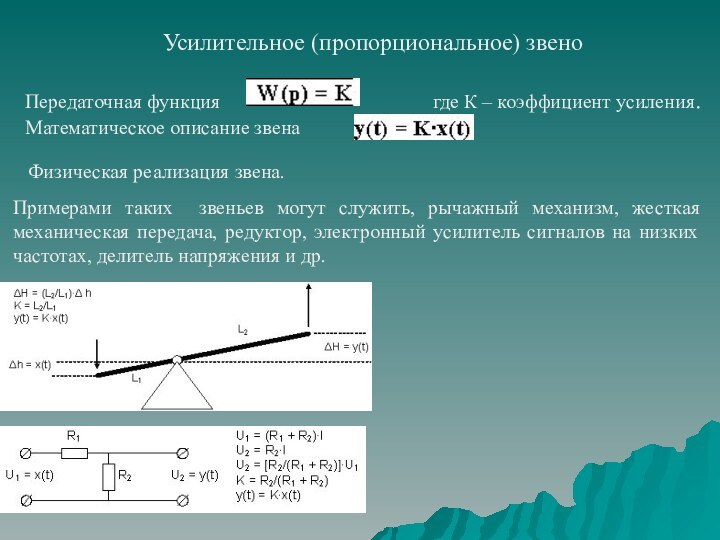
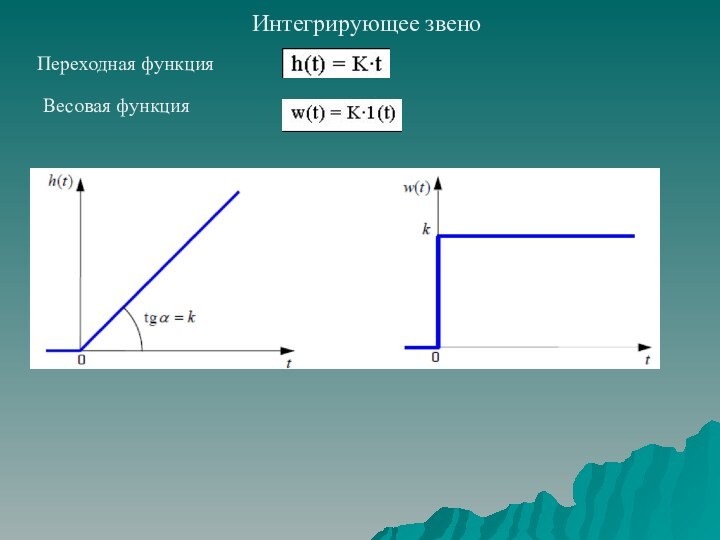
передаточной функции;
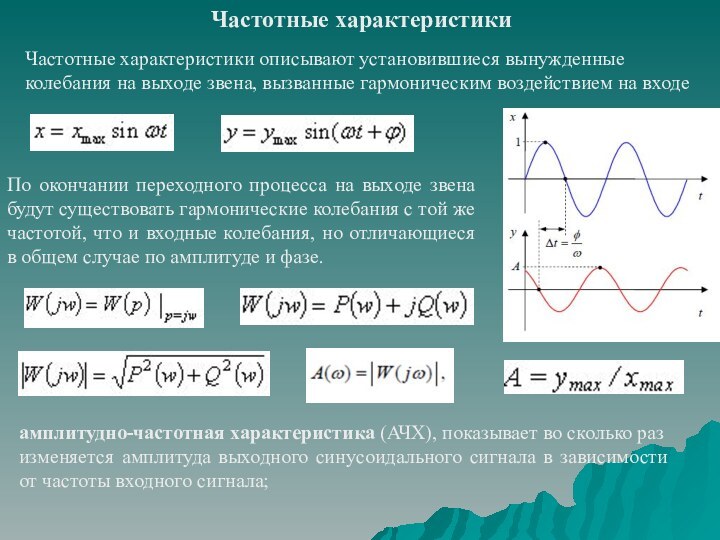
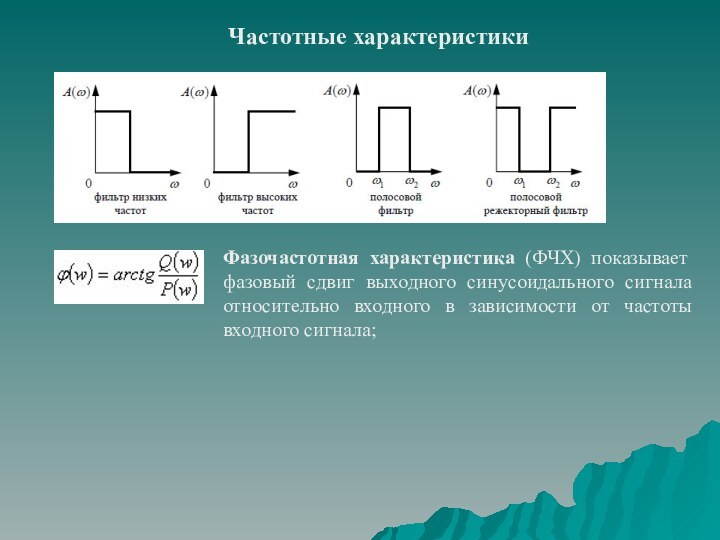
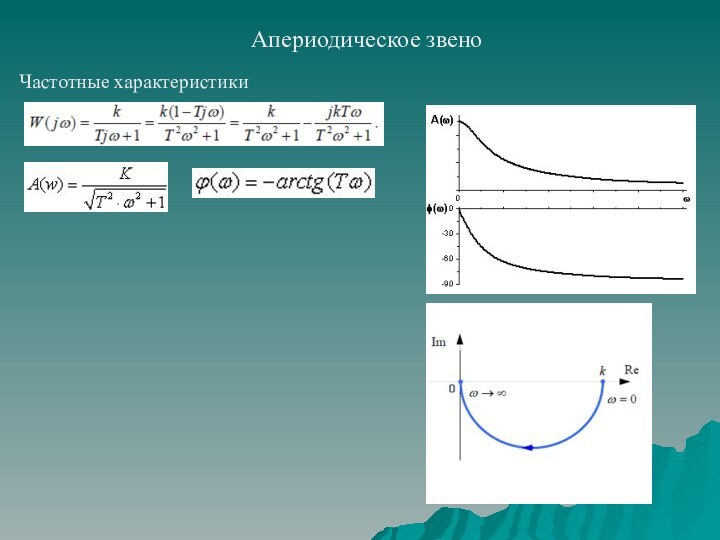
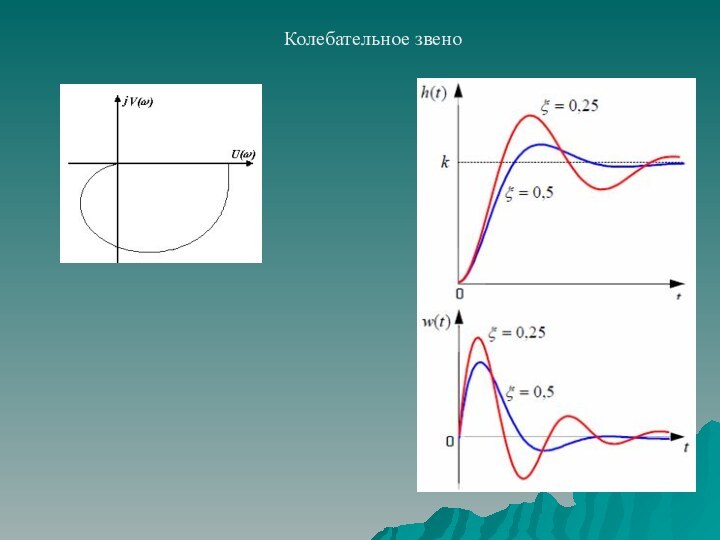
частотных характеристик;
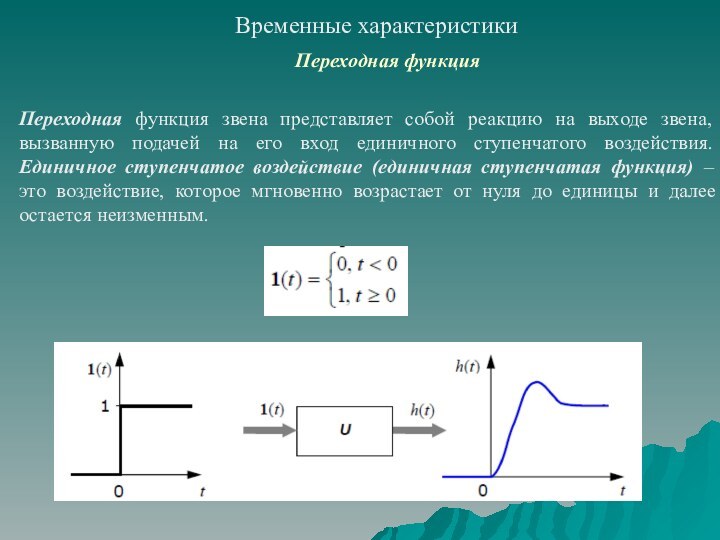
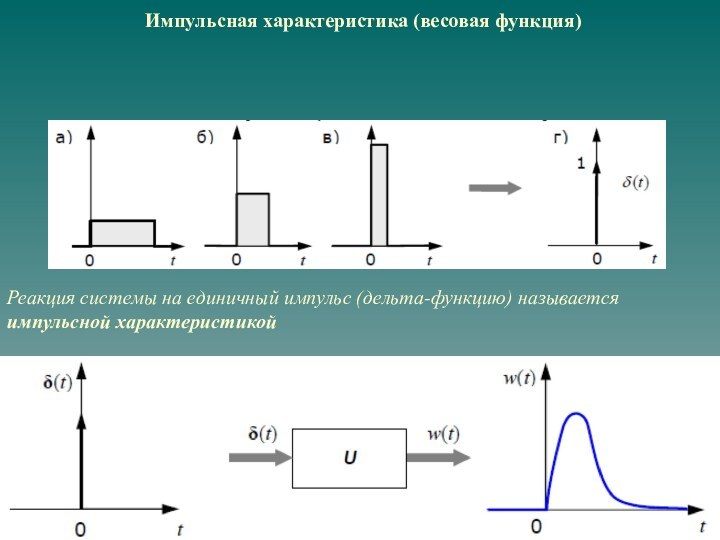
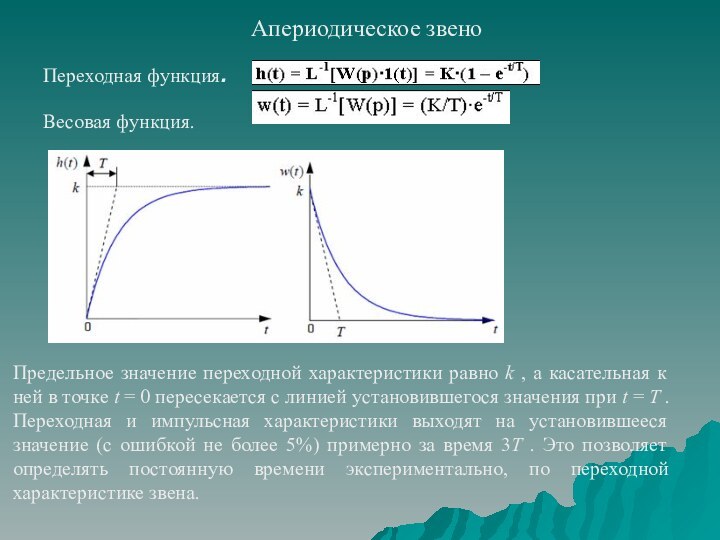
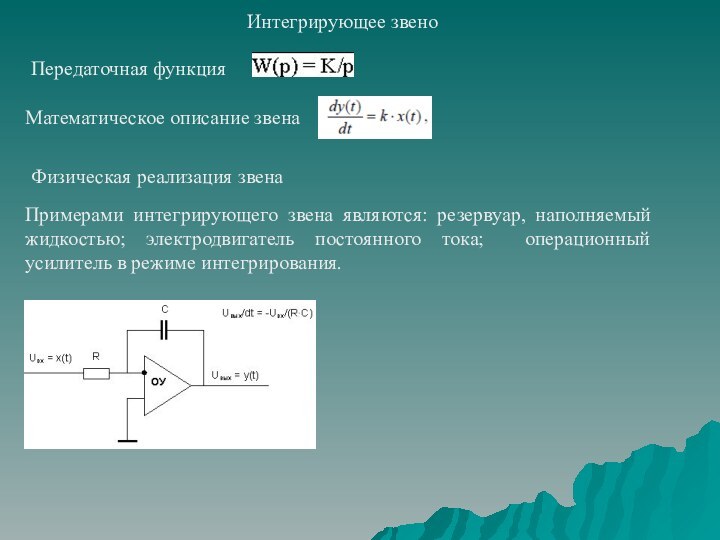
временных характеристик;
Характеристики САУ