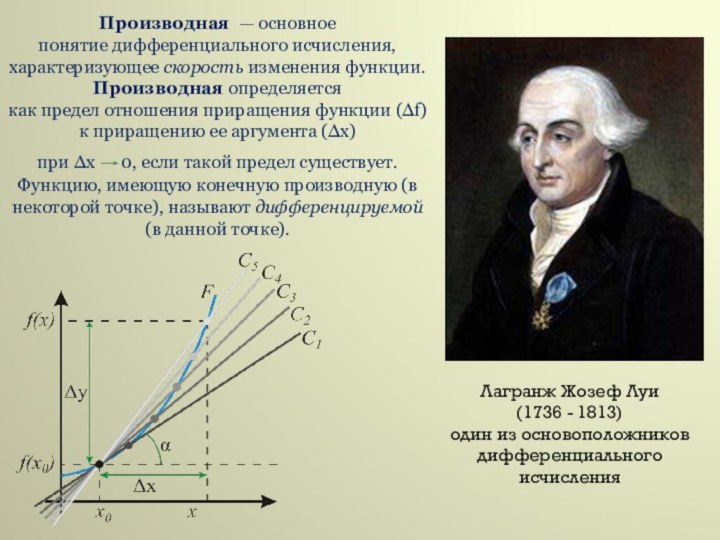
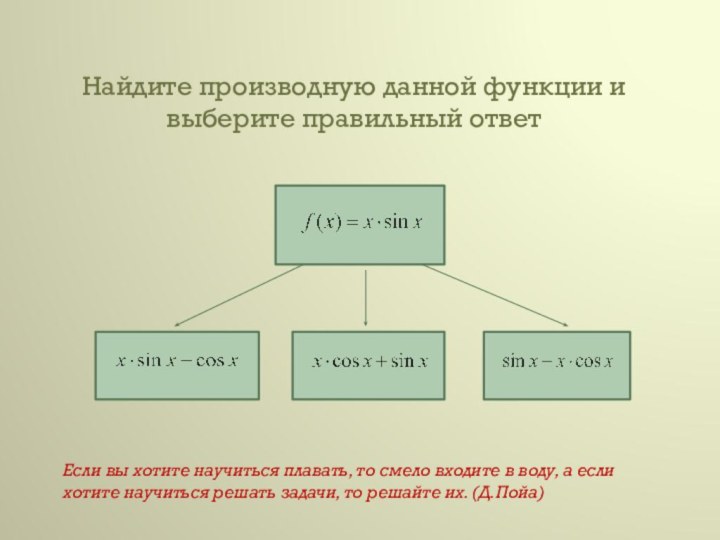
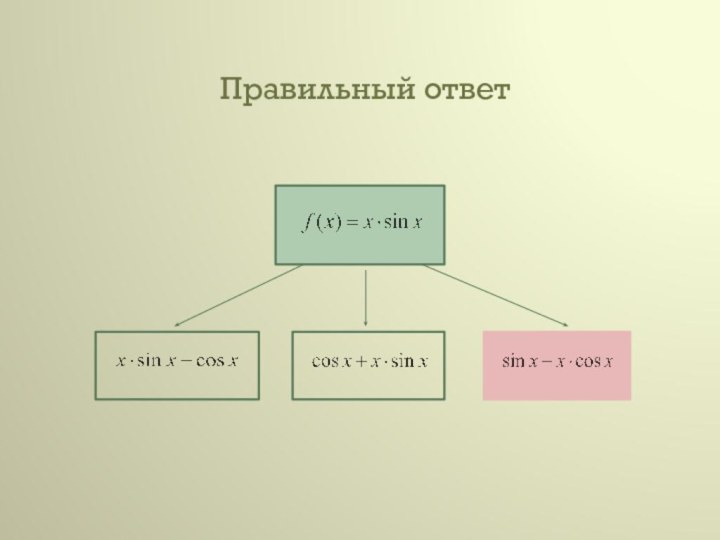
Производная определяется как предел отношения приращения функции (∆f) к приращению ее аргумента
(∆х) при ∆х 0, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).
Лагранж Жозеф Луи
(1736 - 1813)
один из основоположников
дифференциального исчисления