для решения геометрических задач
1
2
3
4
Общая информация о пакете geometry
Команды проверки
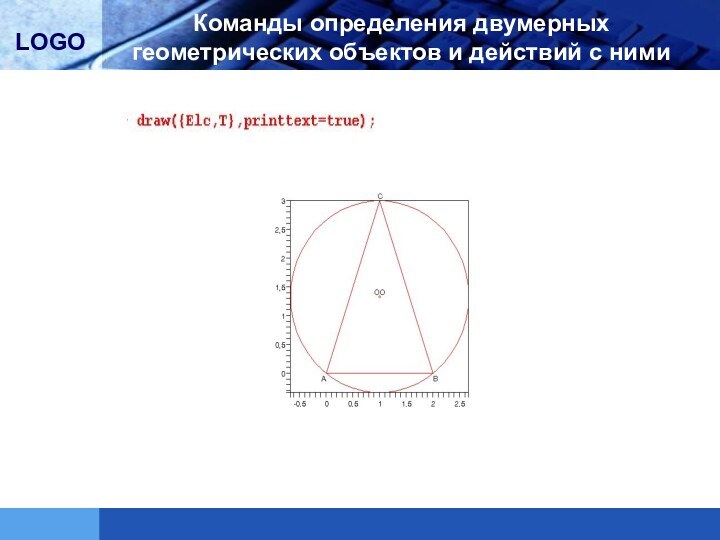
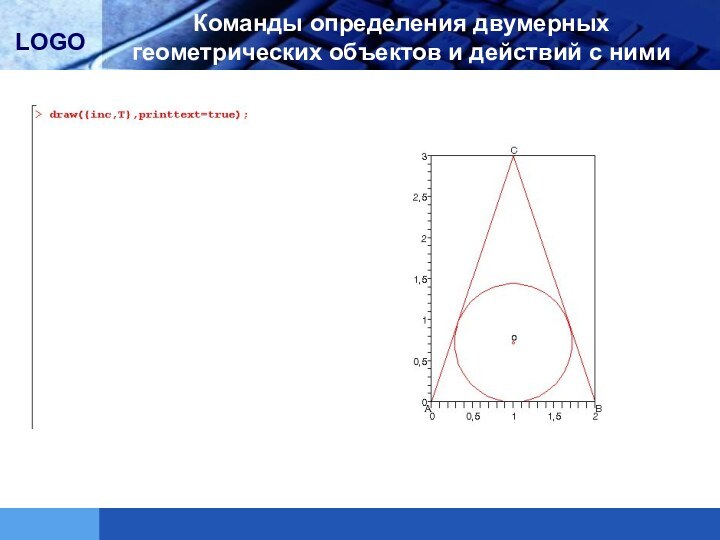
условий для двумерных геометрических объектовКоманды определения двумерных геометрических объектов и действий с ними
Информационные ресурсы












![Презентация по теме Система Maple. Геометрия на плоскости. Возможности пакета geometry для решения геометрических задач AreSimilar(T1,T2); - проверка условия подобия двух треугольников T1 и T2 triangle(name,[p1,p2,p3])](/img/tmb/7/613227/2c3e690b00cbc1d211660da8850d1763-720x.jpg)