- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Деятельностная составляющая современного урока математики
Содержание
- 2. «Единственный путь,
- 3. Простейшие математические знания могут применяться умело и
- 5. Заголовок слайдаТекст слайда
- 6. Основная цель системно – деятельностного подхода в обучении: научить не знаниям, а работе.
- 7. Технология деятельностного подхода: Мотивация (самоопределение) к
- 8. 1 этап. Мотивация (самоопределение) к учебной
- 9. 2 этап. Актуализация и фиксирование индивидуального затруднения
- 10. 4 этап .Построение проекта выхода из затруднения
- 11. 5 этап. Реализация построенного проекта (4–5
- 12. 6 этап. Первичное закрепление с проговариванием во
- 13. 7 этап. Самостоятельная работа с самопроверкой
- 14. 8 этап. Включение в систему знаний и
- 15. 9 Этап Рефлексия учебной деятельности на
- 16. Предложить следующие задания: Оцените свое
- 17. Предложить вопросы: 1. На уроке бывает интересно.
- 18. Методы постановки учебной проблемыПодводящий к теме диалог.Система
- 19. Создание проблем с помощью математических задачЗадачи с
- 20. Задачи с избыточным составом условия.В них введены
- 21. Задачи с неполным составом условия.В них отсутствуют
- 22. Составление задач данного типа.Ученик, ознакомившись с задачей
- 23. Задачи на доказательство.Здесь исследуется собственно творческое обобщение
- 24. Нереальные задачи.Это задачи, лишенные смысла. В данном
- 25. Эвристические задания.Исследуют то, как учащиеся овладевают новым
- 26. Применение технологии деятельностного метода обучения создает условия
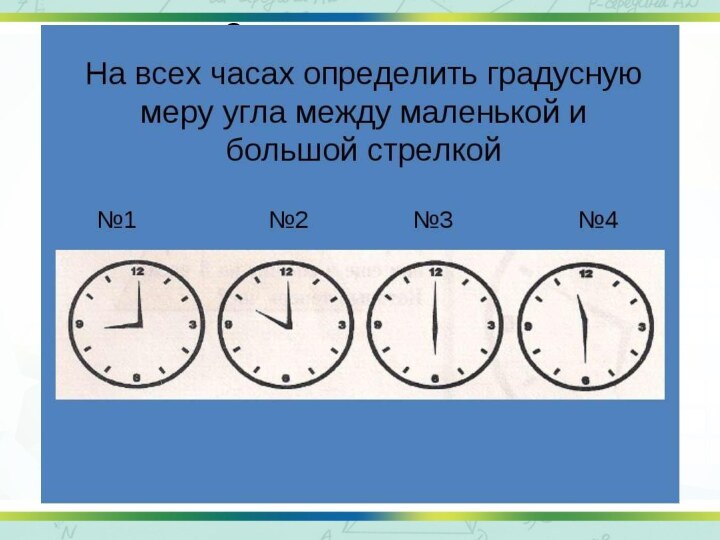
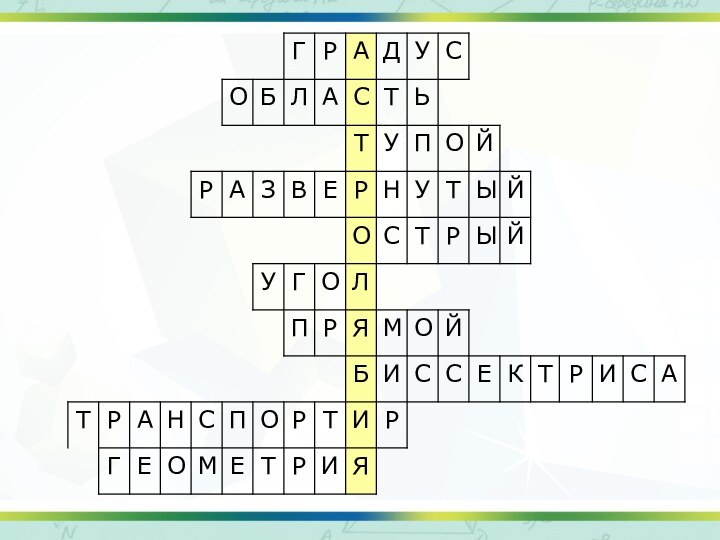
- 27. 90°35°135°90°150°
- 28. Заголовок слайдаТекст слайда
- 29. Работа в группах (практическая) ИЗМЕРЬТЕ ВЕЛИЧИНУ УГЛОВ
- 31. АстролябияАстролябия - сложный угломерный инструмент для определения
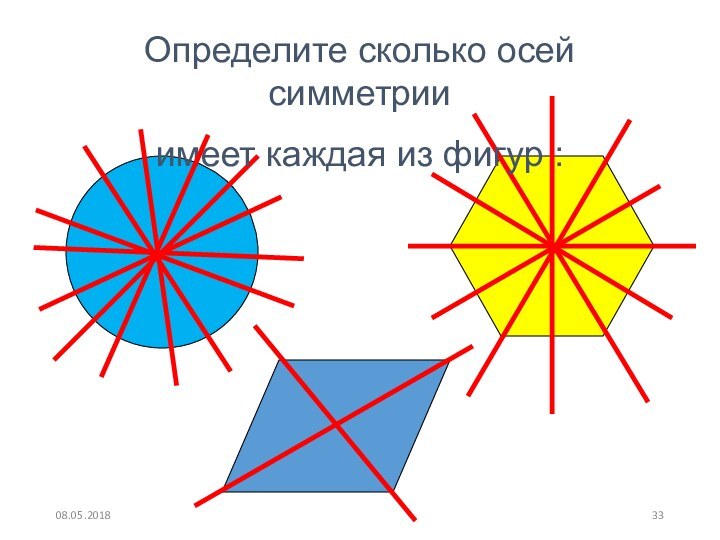
- 33. Определите сколько осей симметрииимеет каждая из фигур :
- 34. Какие из букв имеют вертикальную ось симметрии,
- 35. Скачать презентацию
- 36. Похожие презентации
«Единственный путь, ведущий к знанию – это деятельность»




























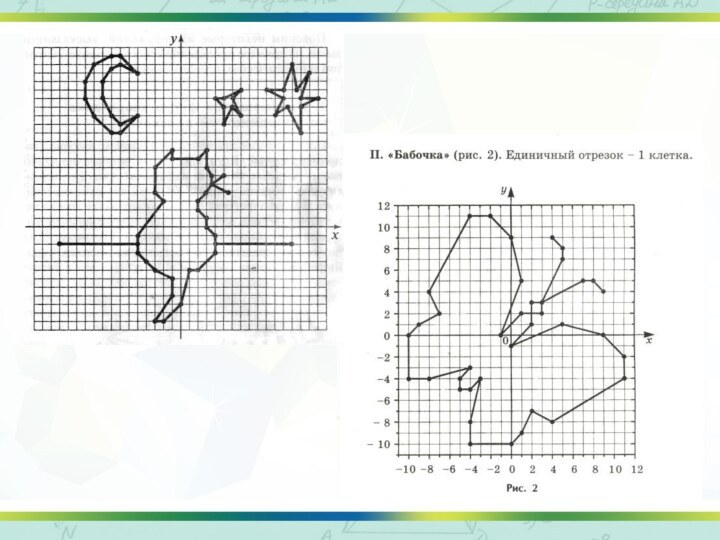


Слайд 3 Простейшие математические знания могут применяться умело и с
пользой
лишь в том случае, если они усвоены творчески,
так, что учащийся видит сам, как можно было бы прийти к ним самостоятельно.
А.Н. Колмогоров
Слайд 7
Технология деятельностного подхода:
Мотивация (самоопределение) к учебной
деятельности.
Актуализация и фиксирование индивидуального затруднения в пробном действии.
Постановка проблемы.
Построение
проекта выхода из затруднения.Реализация построенного проекта.
Первичное закрепление с проговариванием во внешней речи.
Самостоятельная работа с самопроверкой по эталону.
Включение в систему знаний и повторение.
Рефлексия учебной деятельности.
Слайд 8 1 этап. Мотивация (самоопределение) к учебной деятельности
(2–3 мин)
Цель: мотивирование (самоопределить) учащихся к учебной деятельности.
Организация этапа:
1) актуализируются требования к ученику со стороны учебной деятельности («надо»);
2) устанавливаются тематические рамки («могу»).
3) создаются условия для возникновения у ученика внутренней потребности включения в учебную деятельность («хочу»).
Слайд 9 2 этап. Актуализация и фиксирование индивидуального затруднения в
пробном действии (5–7 мин).
3 этап.Постановка проблемы (3–4 мин):
Цель:
- восстановить выполненные операции и зафиксировать (вербально и знаково) место – шаг, операцию, где возникло затруднение;- соотнести свои действия с используемым способом действий (алгоритмом, понятием и т.д.), и на этой основе выявить и зафиксировать во внешней речи причину затруднения и те конкретные знания, умения или способности, которых недостает для решения исходной задачи и задач такого класса или типа вообще.
Слайд 10 4 этап .Построение проекта выхода из затруднения (цель
и тема, способ, план, средство) (3–4 мин)
Цель: построить
проект выхода из затруднения. Организация этапа
На данном этапе учащиеся в коммуникативной форме:
1) ставят цель (целью всегда является устранение возникшего затруднения);
2) согласовывают тему урока;
3) выбирают способ (дополнение или уточнение);
4) строят план достижения цели;
5) определяют средства – алгоритмы, модели, учебник и т.д
Слайд 11 5 этап. Реализация построенного проекта (4–5 мин)
.
Цель: - реализовать построенный проект в соответствии с планом;
- зафиксировать новый способ действия в речи и знаках (с помощью эталона);- организовать решение исходного задания, данного для пробного действия;
- уточнить общий характер нового знания;
- зафиксировать преодоление затруднения.
Слайд 12 6 этап. Первичное закрепление с проговариванием во внешней
речи (5–6 мин)
Цель: организовать усвоение детьми нового способа
действий при решении данного класса задач с их проговариванием во внешней речи Слайд 13 7 этап. Самостоятельная работа с самопроверкой по
эталону. (5–6 мин)
Цель: - проверить на основе сопоставления
с эталоном свое умение применять новое учебное содержание в типовых ситуациях; - организовать рефлексию усвоения нового способа по результатам выполнения самостоятельной работы (особое внимание уделять психологической комфортности).
Слайд 14 8 этап. Включение в систему знаний и повторение.
(5–8 мин)
Цель: - выявить границы применимости нового знания;
- повторить учебное содержание, необходимое для обеспечения содержательной непрерывности.
Слайд 15 9 Этап Рефлексия учебной деятельности на уроке
(итог урока). (2–4 мин)
Цель: - зафиксировать новое содержание,
изученное на уроке; - провести рефлексивный анализ учебной деятельности с точки зрения выполнения требований, известных учащимся;
- оценить собственную деятельность на уроке;
- зафиксировать неразрешенные затруднения как направления будущей учебной деятельности;
- обсудить и записать домашнее задание .
Слайд 16 Предложить следующие задания: Оцените свое отношение к
учебному предмету математика.
А. Вы всегда испытываете
такое отношение к предмету – 2 балла; Б. Вы иногда испытываете такое отношение к предмету – 1 балл;
В. Никогда не испытываете такого отношения к предмету – 0 баллов.
Слайд 17
Предложить вопросы:
1. На уроке бывает интересно. Нравится
учитель. Нравится получать хорошие оценки.
2. Родители заставляют учиться.
Учу, т.к. это мой долг. Предмет полезен для жизни.3. Узнаю много нового. Заставляет думать.
Получаю удовольствие, работая на уроке.
4.Легко дается. Стремлюсь узнать больше, чем требует учитель.
Слайд 18
Методы постановки учебной проблемы
Подводящий к теме диалог.
Система посильных
ученику вопросов и заданий, которые шаг за шагом приводят
ученика к осознанию темы урока.Не требует создания проблемной ситуации, хорошо выстраивается «от повторения».
Мотивирующие приемы.
Яркое пятно: сказки, легенды, фрагменты из художественной литературы, случаи из истории науки, культуры и повседневной жизни, шутки и др. интригующий материал.
Актуальность: обнаружение смысла, значимости предлагаемой темы урока для самих учащихся.
Побуждающий от проблемной ситуации диалог.
Слайд 19
Создание проблем с помощью математических задач
Задачи с несформулированным
вопросом.
Вопрос не формулируется ни прямо ни косвенно, но он
логически вытекает из данных в задаче математических отношений. Такие задачи позволяют выяснить, видит ли учащийся в них лишь совокупность разрозненных данных, или задача для него изначально существует как комплекс взаимосвязанных величин.“Автомобиль прошел 630 км со
скоростью 70 км/ч. (Какое время он
затратил на путь?)”
Слайд 20
Задачи с избыточным составом условия.
В них введены дополнительные,
ненужные, не имеющие значения показатели. Учащиеся должны уметь из
совокупности данных им величин выделить именно те, которые представляют собой систему отношений, составляющих существо задачи, и являются необходимыми и достаточными для ее решения.“Расстояние между двумя пристанями 120 км. Теплоход, двигаясь со скоростью 30 км/ч, прошел этот путь за 4 часа. На обратном пути он прошел то же расстояние за 5 часов. С какой скоростью шел теплоход на обратном пути? (Лишнее данное – расстояние между пристанями.)”
Слайд 21
Задачи с неполным составом условия.
В них отсутствуют некоторые
данные, вследствие чего дать точный ответ на вопрос задачи
не представляется возможным. Цель таковых – узнать, “схватывают” ли ученики в процессе восприятия условия задачи ее формальную структуру, способны ли обнаружить неполноту данных.“Две лодки отошли одновременно навстречу друг другу от двух пристаней. Одна лодка проходила в час 15 км, а другая – 10 км. Найти расстояние между пристанями. (Не указано через какое время лодки встретились.)”
Слайд 22
Составление задач данного типа.
Ученик, ознакомившись с задачей или
решив ее, должен самостоятельно составить другие задачи:
а) Аналогичную данной
с измененными числовыми данными;
б) Задача другого предметного содержания, и с другими числовыми показателями;
в) Задача другого предметного содержания, представленная в общем виде.Проверяется, сможет ли ученик произвести самостоятельное обобщение ряда объектов в результате анализа лишь одного объекта данного рода.
“Велосипедист должен попасть в место назначения к определенному сроку. Известно, что если он поедет со скоростью 15 км/ч, то приедет на час раньше, а если скорость будет 10 км/ч, то он опоздает на час. С какой скоростью должен ехать велосипедист, чтобы приехать вовремя?”
Слайд 23
Задачи на доказательство.
Здесь исследуется собственно творческое обобщение метода
рассуждения, перенос усвоенных принципов доказательства на решение аналогичных, но
более сложных мыслительных задач.“Доказать, что при увеличении скорости тело пройдет одно и то же расстояние за меньшее время.”
Слайд 24
Нереальные задачи.
Это задачи, лишенные смысла. В данном случае
можно проследить особенности обобщения математического материала, проявляющиеся как в
области восприятия, так и в области переработки и хранения в памяти.“Скорость парохода 20 км/ч. Расстояние от пункта А до пункта В он прошел по течению за 3 часа. Обратно пароход шел против течения со скоростью 30 км/ч. Сколько времени он затратил на путь от пункта В до пункта А?”
Слайд 25
Эвристические задания.
Исследуют то, как учащиеся овладевают новым для
них материалом, как самостоятельно устанавливают отношения и функциональные зависимости,
производят самостоятельные обобщения.“Путь, который турист проехал поездом, на 150 км больше пути, который он проехал на пароходе, и на 750 км. Больше пути, пройденного им пешком. Определить длину всего пути, если известно, что пешком он прошел в три раза меньше, чем проехал на пароходе.”
Слайд 26 Применение технологии деятельностного метода обучения создает условия для
формирования у ребенка готовности к саморазвитию, помогает формировать устойчивую
систему знаний и систему ценностей (самовоспитание).
Слайд 29
Работа в группах
(практическая)
ИЗМЕРЬТЕ ВЕЛИЧИНУ
УГЛОВ НА ЛУЧАХ СОЛНЫШКА
1
группа
Задание:
2 группа
Задание:
ИЗМЕРЬТЕ ВЕЛИЧИНЫ УГЛОВ
НА
РИСУНКЕ
Слайд 31
Астролябия
Астролябия - сложный угломерный инструмент для определения положения
звезд. Он появился еще в Древней Греции. К IX
в. астролябия получила широкое распространение в странах арабского Востока, где с ее помощью решали многие практические задачи. Например, определяли время, продолжительность дня и ночи, измеряли горизонтальные углы на поверхности Земли, осуществляли различные математические вычисления.Слайд 34 Какие из букв имеют вертикальную ось симметрии, какие
горизонтальную, какие имеют
и вертикальную, и горизонтальную оси симметрии ?Какие
из букв не имеют осей симметрии ?А Б В Г Д Е Ж З И
К Л М Н О П Р С Т