- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по дисциплине Дискретная математика на тему Булевы функции
Содержание
- 2. История булевых функцияБулевы функции получили своё название
- 3. Основные понятия
- 4. Основные понятияТаблицы, в которых каждой интерпретации поставлено
- 5. Элементарные функцииК элементарным функциям обычно относят: функцию
- 6. Функции 2-ух переменных
- 7. ФормулыТак же, как составные высказывания строятся из
- 8. Приоритет операцийЕсли в формуле отсутствуют скобки, то операции выполняются в следующей последовательности:1.Отрицание2.Конъюнкция3.Дизъюнкция4.Импликация5.Эквивалентность.
- 9. Основные определения Формулы называются равносильными, если реализуют
- 10. Аксиомы булевы алгебры Аксиомы конъюнкции Аксиомы дизъюнкции
- 11. Законы булевой алгебрыПоглощение A + (A*B) = A A*(A
- 12. Законы булевой функцииДополнение
- 13. Контрольные вопросыПриведи примеры логических функций одной переменной.Приведи
- 14. Скачать презентацию
- 15. Похожие презентации
История булевых функцияБулевы функции получили своё название по имени английского математика Дж. Буля (02.11.1815–08.12.1864). С давних времён эти функции играют важную роль в вопросах оснований математики и математической логике. С середины 20-го века булевы функции широко













Слайд 4
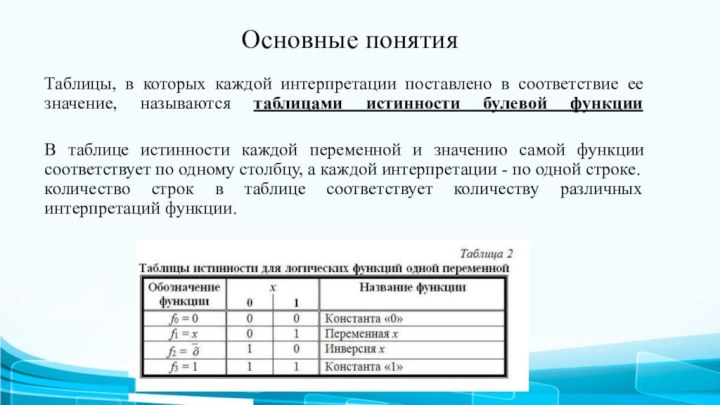
Основные понятия
Таблицы, в которых каждой интерпретации поставлено в
соответствие ее значение, называются таблицами истинности булевой функции
В таблице
истинности каждой переменной и значению самой функции соответствует по одному столбцу, а каждой интерпретации - по одной строке. количество строк в таблице соответствует количеству различных интерпретаций функции.
Слайд 5
Элементарные функции
К элементарным функциям обычно относят: функцию инверсии
(отрицания), конъюнкцию, дизъюнкцию, импликацию, штрих Шеффера и стрелку Пирса.
Новые
функции можно получить из известных функций либо путем перенумерации аргументов, либо путем подстановки в функцию новых функций вместо аргументов. Функция, полученная с помощью этих правил, называется суперпозицией функций.
Слайд 7
Формулы
Так же, как составные высказывания строятся из более
простых, с помощью логических операций, можно комбинировать булевы переменные
с помощью булевых операций, получая булевы выражения, которые называются формулами.Всякой формуле однозначно соответствует некоторая функция, при этом говорят, что формула реализует функцию.
Слайд 8
Приоритет операций
Если в формуле отсутствуют скобки, то операции
выполняются в следующей последовательности:
1.Отрицание
2.Конъюнкция
3.Дизъюнкция
4.Импликация
5.Эквивалентность.
Слайд 9
Основные определения
Формулы называются равносильными, если реализуют одну
и ту же функцию. Формула называется тождественно истинной или тавтологией,
если она реализует тождественную единицу при любых значениях булевых переменных. Формула называется тождественно ложной, если она реализует тождественный ноль при любых значениях булевых переменных.
Слайд 11
Законы булевой алгебры
Поглощение
A + (A*B) = A A*(A +
B) = A
Аннулирование
A + 1 = 1 A*0 = 0
Ассоциативность
(A+B)+C=A+(B+C) (A*B)*C=A*(B*C) Коммутативность (перестановка)
A + B = B + A A*B=B*A
Двойное отрицание ¬¬A=A
Слайд 12
Законы булевой функции
Дополнение
A + ¬A = 1 A*¬A = 0 Правило Де Моргана ¬(A + B) = ¬A*¬B ¬(A*B) = ¬A + ¬B Тождественность A + 0 = A A*1=A Тавтология A*A = A A + A = A
Слайд 13
Контрольные вопросы
Приведи примеры логических функций одной переменной.
Приведи примеры
логических функций двух переменных.
Сколько может быть полностью определенных n
переменных?Что такое булевы переменные?
Приведи примеры логических операций, используемые при формировании двух переменных.
Приведите структуру таблицы истинности.