м
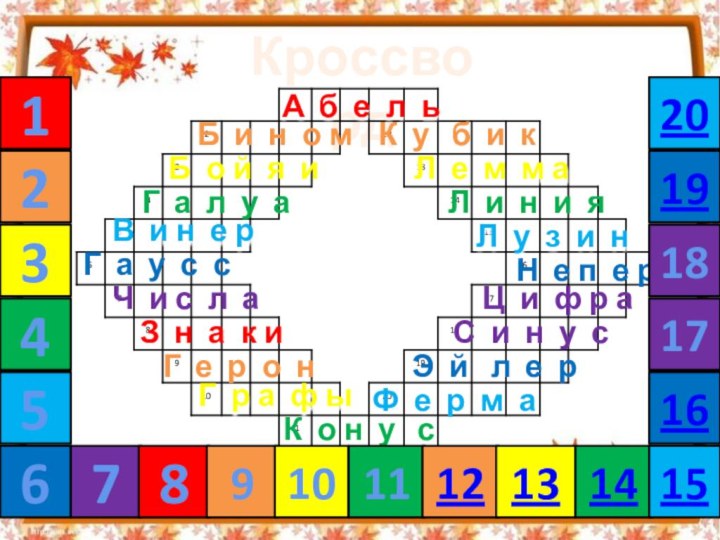
Б о й я и
Г а л у
аВ и н е р
Г а у с с
Ч и с л а
Ц и ф р а
Г е р о н
Г р а ф ы
К о н у с
Ф е р м а
Э й л е р
С и н у с
А б е л ь
Н е п е р
Л у з и н
Л и н и я
Л е м м а
К у б и к
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20