- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Простые и составные числа
Содержание
- 2. История чиселЧИСЛО - абстракция, используемая для количественной
- 3. «Палочная» система для обозначения чисел использовался всего
- 4. В Вавилонской системе используются прямой клин, для
- 5. Существовала также славянская система. Цифры в ней
- 6. История гласит, что прообразом современных арабских цифр
- 7. Арабские цифры значительно экономили время и материалы
- 8. Понятие простого числа было введено математиками Древней
- 9. Как определить, какое число простое, а какое
- 10. Скачать презентацию
- 11. Похожие презентации








Слайд 3 «Палочная» система для обозначения чисел использовался всего один
элемент – палочка. Недостатки этой системы очевидны, слишком сложно
и можно ошибиться.Во второй половине третьего тысячелетия до нашей эры возникла древнеегипетская система. В ней единицы, десятки, сотни, тысячи и т.д. записывались определенными символами, которые повторялись не более девяти раз.
На рисунке число 345
- сотни, - десятки, - единицы.
Слайд 4 В Вавилонской системе используются прямой клин, для обозначения
десятков. Эта система внесла большой вклад в развитие цифр
и систем счисления.Римская система нам хорошо знакома. В ней для обозначения цифр используются латинские буквы.
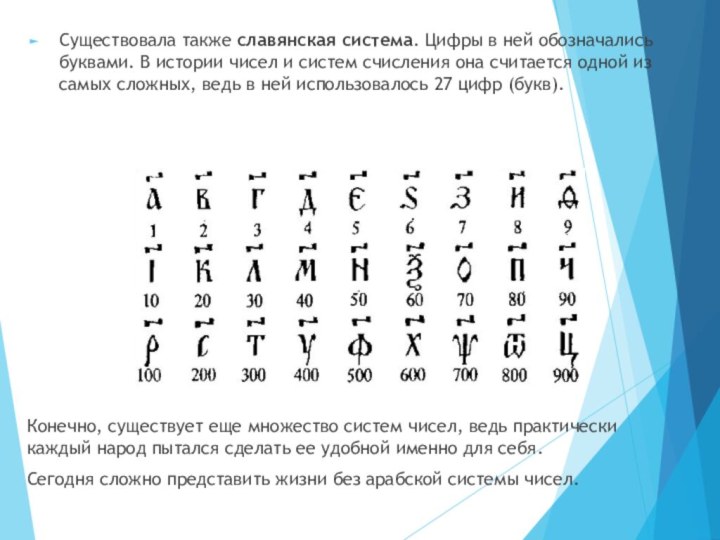
Слайд 5 Существовала также славянская система. Цифры в ней обозначались
буквами. В истории чисел и систем счисления она считается
одной из самых сложных, ведь в ней использовалось 27 цифр (букв).Конечно, существует еще множество систем чисел, ведь практически каждый народ пытался сделать ее удобной именно для себя.
Сегодня сложно представить жизни без арабской системы чисел.
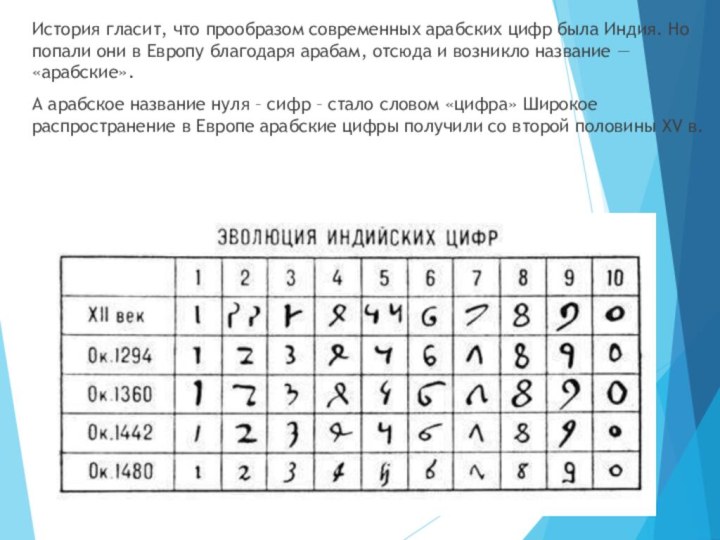
Слайд 6 История гласит, что прообразом современных арабских цифр была
Индия. Но попали они в Европу благодаря арабам, отсюда
и возникло название — «арабские».А арабское название нуля – сифр – стало словом «цифра» Широкое распространение в Европе арабские цифры получили со второй половины XV в.
Слайд 7 Арабские цифры значительно экономили время и материалы для
письма. Один арабский ученый предложил обозначать цифру символом с
определенным количеством углов. Количество углов должно равняться значению цифры. Например, «0» — «ничто», углов нет; 1 – 1 угол; 2 – 2 угла и т.д. Слово «цифра» также позаимствовано из арабских языков, где оно звучало как «сыфр», и обозначало «ничто», «пустота». У «сыфр» был синоним – «шунья». На протяжении веков «0» называли именно так. До тех пор, пока не появилось латинское «нуллум» («ничто»), как мы и называем «ноль».Слайд 8 Понятие простого числа было введено математиками Древней Греции.
Математики школы Пифагора (500 г. до н.э. – 300
г. до н.э.) интересовались мистическими и нумерологическими свойствами чисел. Они понимали идею простоты чисел и изучали совершенные и дружественные числа. В своей книге “Начал” Евклид доказывает, что существует бесконечно много простых чисел.Простые числа - большие единицы, которые не делятся ни на одно натуральное число, кроме единицы и самого себя.
Пример: 2,3,5,7,11,13,17.
Составные числа, это такие числа, которые имеют другие делители, кроме единицы и самого себя.
Пример 21/1,3,7,21
Слайд 9 Как определить, какое число простое, а какое нет?
Первый в истории метод поиска, позволяющий найти все простые
числа в любом числовом отрезке, предложил в III в. до н. э. Эратосфен (метод называется «решето Эратосфена»).Сначала вычеркивают все числа, делящиеся на 2 (исключая само число 2). Потом берут первое из оставшихся чисел (а именно 3). Ясно, что это число - простое. Вычеркивают все идущие после него числа, делящиеся на 3. Первым оставшимся числом будет 5. Вычеркивают все идущие после него числа, делящиеся на 5, и т.д.