Презентация на тему Вывод канонического уравнения эллипса

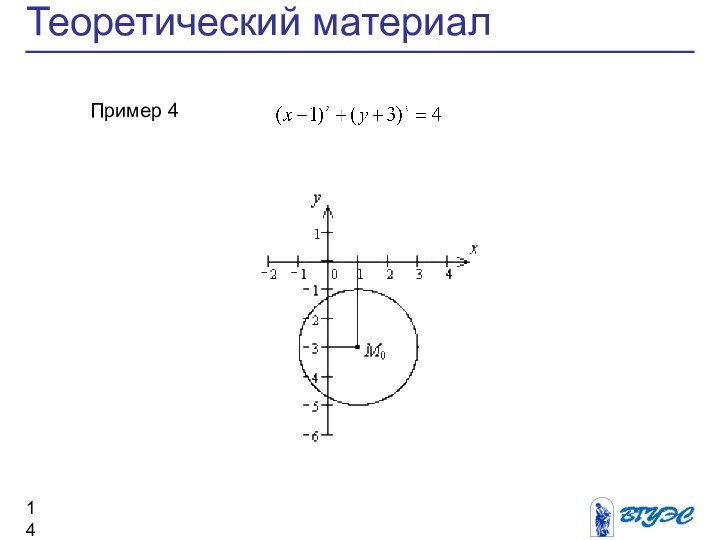
канонического уравнения эллипса»
Задачи:
Рассмотреть свойства эллипса
Исследовать зависимость формы эллипса

от вида уравнения
Установить связь между эллипсом и окружностью

A, B,C, D, E и F – постоянные действительные

числа,
причем, A, B и C одновременно не равны нулю

Уравнением кривой второго порядка
называется уравнение вида

прямоугольной системе координат имеет вид:

называются соответственно большой и малой
полуосями эллипса. Эллипс содержится

в прямоугольнике


Вершинами эллипса являются точки

системы координат
являются осями симметрии эллипса, а начало координат

– его
центром симметрии

3) Если эллипс не является окружностью, то координатные оси
канонической системы – единственные оси симметрии

4) Эллипс есть множество точек, сумма расстояний от которых до
двух данных точек (фокусов) постоянна (равна заданному числу)

где
называются соответственно правым и левым фокусами эллипса.
Величина называется фокусным расстоянием.

расстояний
от которых до данной точки (фокуса эллипса) и

до данной прямой
(одноименной с фокусом директрисы эллипса) постоянно (равно
эксцентриситету эллипса)

Число называется эксцентриситетом эллипса

Правой и левой директрисой эллипса называются прямые

из фокусов эллипса с зеркальной
«поверхностью» точечный источник света,

то все лучи после
отражения от «поверхности» эллипса сойдутся в другом его фокусе

является частным случаем эллипса при

Эксцентриситет окружности равен нулю. Чем ближе значение
эксцентриситета эллипса к нулю, тем больше форма эллипса
приближается к форме окружности.

Окружность, центром которой является точка ,
определяется уравнением

Пример 1

между уравнением эллипса и его формой
Эксцентриситет эллипса
Директрисы и фокусы

эллипса
Альтернативные определения эллипса