- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Презентационный материал Система счисления
Содержание
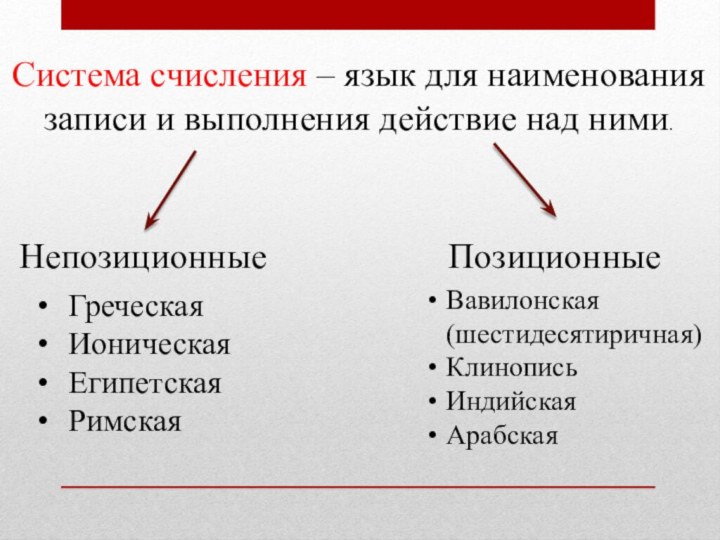
- 2. Система счисления – язык для наименования записи и выполнения действие над ними.НепозиционныеПозиционныеГреческаяИоническаяЕгипетскаяРимская Вавилонская (шестидесятиричная)КлинописьИндийскаяАрабская
- 3. Десятичная система счисления — позиционная система счисления по целочисленному основанию 10.
- 4. Свойства позиционной десятичной системы счисленияЗначение цифры зависит
- 5. Запись чисел в десятичной позиционной системе счисления:956-сокращенная
- 6. Формы записи чисел:однозначного числа :a0Двузначного числа:a1*10+a0Трехзначного числа:a2*10^2+a1*10+a0
- 7. Теорема: Любое натуральное число x можно представить
- 8. Теорема существования: существует такое натуральное число x,
- 9. Теорема единственности: Если запись X=аn*10^n+an-1*10^n-1+…+a2*10^2+ai*10+a0 существует, то она единственна
- 10. Двоичная система счисления — позиционная система счисления с основанием 2.
- 11. Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3.
- 12. Основанием пятеричной системы является цифра 5. Соответственно,
- 13. Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления
- 14. Шестнадцатеричная система счисления — позиционная система счисления по целочисленному основанию
- 15. (1987)10 = (11111000011)2
- 16. Скачать презентацию
- 17. Похожие презентации
Система счисления – язык для наименования записи и выполнения действие над ними.НепозиционныеПозиционныеГреческаяИоническаяЕгипетскаяРимская Вавилонская (шестидесятиричная)КлинописьИндийскаяАрабская












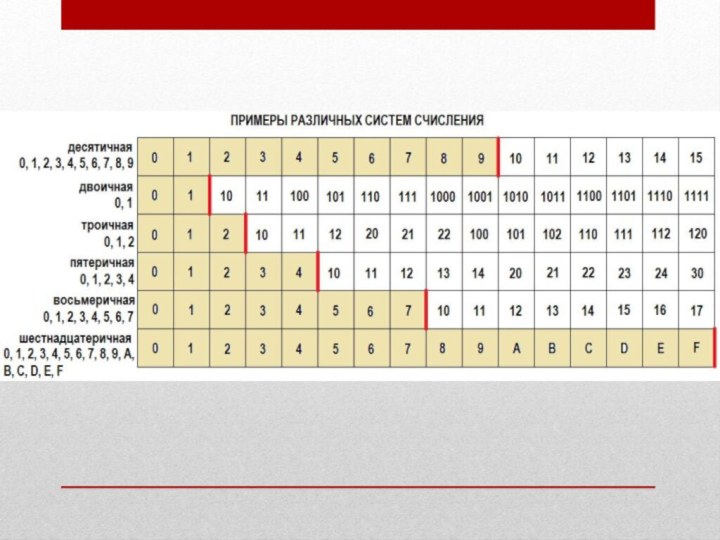
Слайд 3 Десятичная система счисления — позиционная система счисления по целочисленному основанию 10. Одна
из наиболее распространённых систем. В ней используются цифры 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, называемые арабскими
цифрами.
Слайд 4
Свойства позиционной десятичной системы счисления
Значение цифры зависит от
ее места
Для записи чисел используются 10 цифр
(от 0
до 9)Соотношение между разрядными единицами равно 10( т.е 10 ед.низшего разряда -1 ед.высшего)
Слайд 5
Запись чисел в десятичной позиционной системе счисления:
956-сокращенная запись
900+50+6=9*10^2+5*10+6
– систематическая форма записи натурального числа
Систематической формой записи натурального
числа x называется его представление в виде суммы степеней с основанием 10 и коэфициентов.X=аn*10^n+an-1*10^n-1+…+a2*10^2+ai*10+a0
ai-коэфициенты (цифры)
0
Слайд 6
Формы записи чисел:
однозначного числа :a0
Двузначного числа:a1*10+a0
Трехзначного числа:a2*10^2+a1*10+a0
Слайд 7 Теорема: Любое натуральное число x можно представить в
виде суммы степеней с основанием 10, такая запись единственна
Слайд 8 Теорема существования: существует такое натуральное число x, существует
такое натуральное число ч, которое можно представить в виде
суммы степеней
Слайд 9
Теорема единственности: Если запись
X=аn*10^n+an-1*10^n-1+…+a2*10^2+ai*10+a0
существует, то она
единственна
Слайд 10
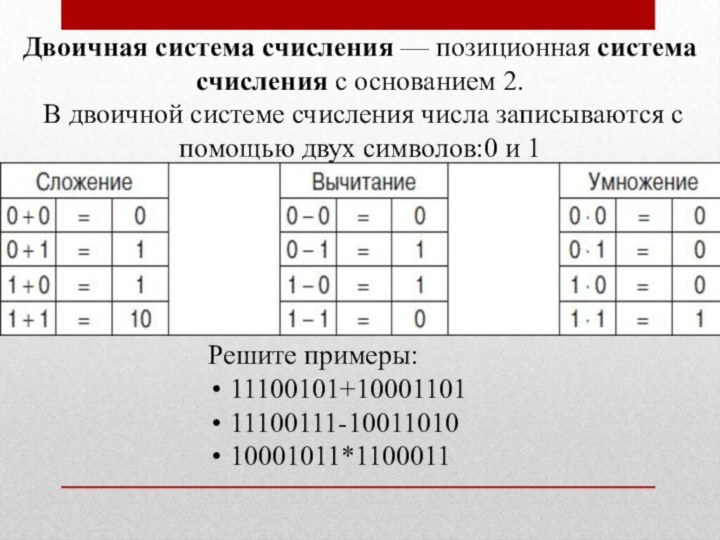
Двоичная система счисления — позиционная система счисления с основанием 2.
В
двоичной системе счисления числа записываются с помощью двух символов:0
и 1Решите примеры:
11100101+10001101
11100111-10011010
10001011*1100011
Слайд 11
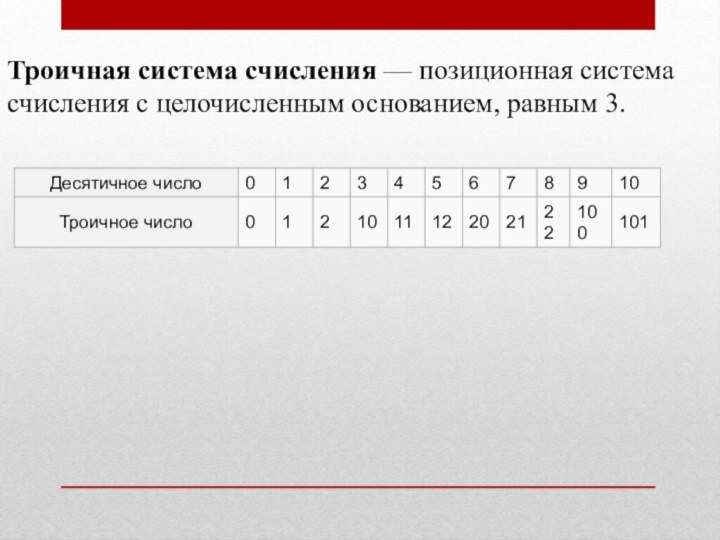
Троичная система счисления — позиционная система счисления с целочисленным основанием, равным 3.
Слайд 12 Основанием пятеричной системы является цифра 5. Соответственно, это число представляет
собой один разряд
132 в пятеричной системе представляет собой 2•5^0
+ 3•5¹ + 1•5² = 2 + 15 + 25 = 42 в десятеричной.
Слайд 13 Восьмеричная система счисления — позиционная целочисленная система счисления с основанием 8. Для представления чисел
в ней используются цифры от 0 до 7.
08 = 0002
18 =
001228 = 0102
38 = 0112
48 = 1002
58 = 1012
68 = 1102
78 = 1112
Таблица перевода восьмеричной системы в двоичную





























