Презентация на тему Три признака равенства треугольников

сторону, лежащую против угла NDL:
3) угол, лежащий против стороны

DN:
4) угол, лежащий против стороны DL:
5) углы, прилежащие к стороне NL: и

Треугольник

Рис. 1

= OMN

Решение:
1) Рассмотрим OLF и

:
а) OL = - по условию,
б) OF = - по условию,

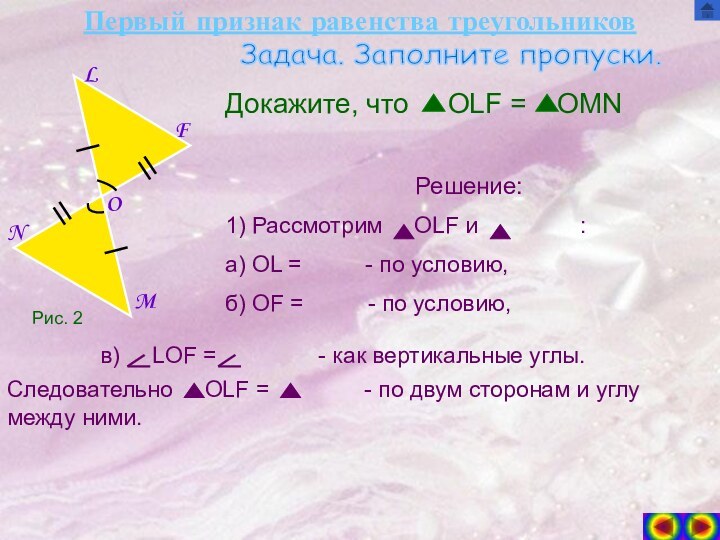
Задача. Заполните пропуски.

Следовательно OLF = - по двум сторонам и углу между ними.

Рис. 2

в) LOF = - как вертикальные углы.

ARS = BRS

а) Сторона

= - по условию.
б) Сторона = - общая сторона.
в) = - по условию.
г) Следовательно, ARS = - по двум
и углу .
2) Т. к. ASR= BSR, то соответственные стороны и углы равны, BR = AR = 18 см, BRS = ARS =

15˚

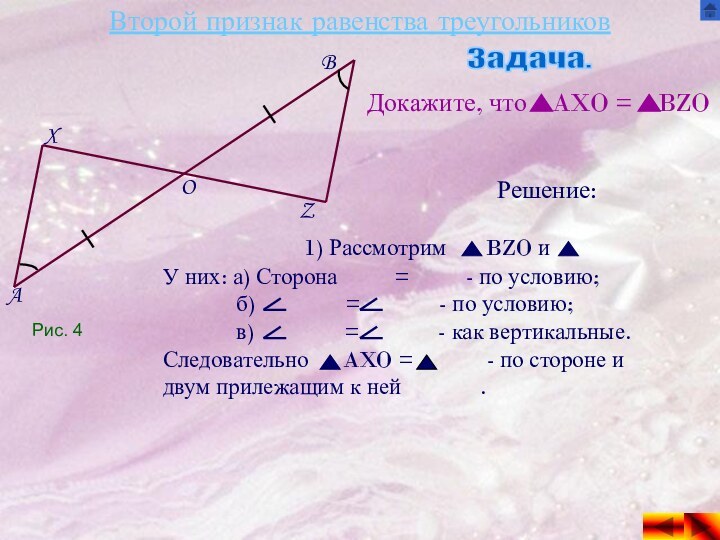
Решение:

1) Рассмотрим ARS и

Рис. 3

= BZO

Решение:
A
X
B
Z
O
1) Рассмотрим BZO и

У них: а) Сторона = - по условию;
б) = - по условию;
в) = - как вертикальные.
Следовательно AXO = - по стороне и двум прилежащим к ней .

Рис. 4

ADF
а) Докажите, что ADF =

BDF;
б) Найдите сторону BD и DBF.
Решение:
а) Рассмотрим ADF и .
У них: 1) = - общая сторона;
2) = - по условию;
3) = , так как DF –

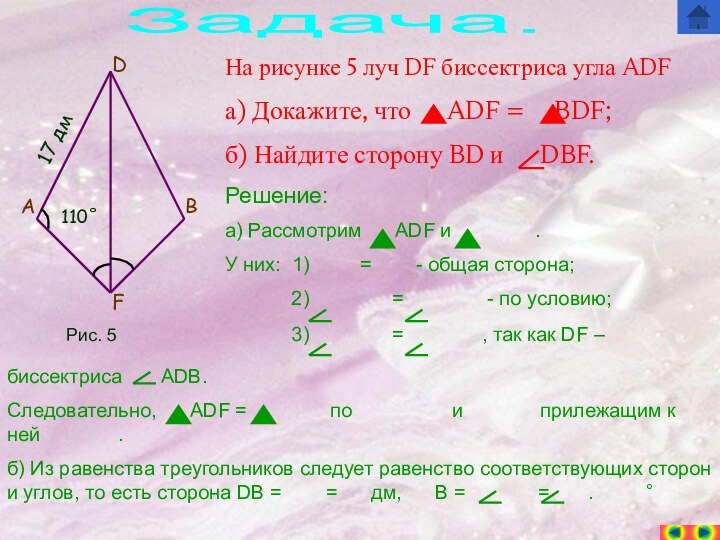
17 дм

110˚

биссектриса ADB.
Следовательно, ADF = по и прилежащим к ней .
б) Из равенства треугольников следует равенство соответствующих сторон и углов, то есть сторона DB = = дм, B = = .

˚

Рис. 5

CAN = BAN
б) Найдите

ABN.

Решение:
а) Рассмотрим и BAN.
У них: 1) AC = - по условию;
2) CN = - по условию;
3) AN = AN – общая сторона.
Значит, CAN = - по трем .
б) Из равенства треугольников CAN и BAN следует равенство соответствующих углов, то есть ABN = = .

Рис. 6

˚

AC=DF, углы A и D равны (рис. 7). Докажем,

что ABC = DEF.
Так как A = D, то треугольник ABC можно наложить на треугольник DEF так, что вершина A совместится с вершиной D, а стороны AB и AC наложатся соответственно на лучи DE и DF. Поскольку AB=DE, AC=DF, то сторона AB совместится со стороной DE, а сторона AC – со стороной DF; в частности, совместятся точки B и E, C и F. Следовательно, совместятся стороны BC и EF. Итак, треугольники ABC и DEF полностью совместятся, значит, они равны.

Рис. 7

C

A

B

D

E

F

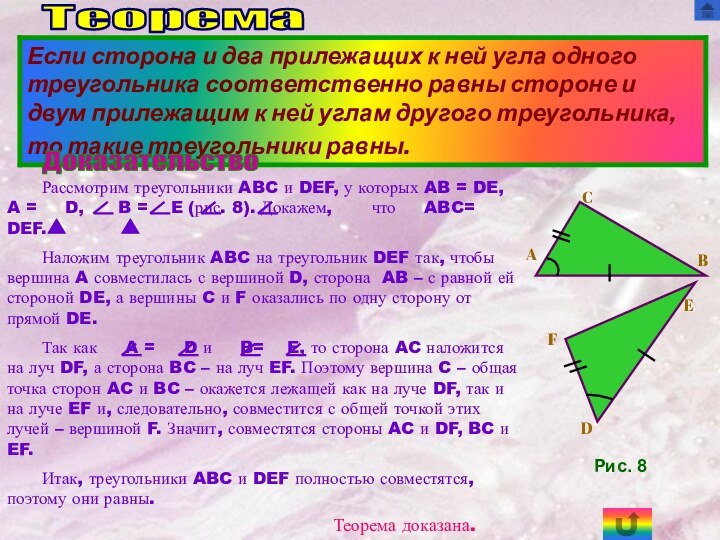
Теорема

Доказательство

Теорема доказана.

AB = DE, A =

D, B = E (рис. 8). Докажем, что ABC= DEF.
Наложим треугольник ABC на треугольник DEF так, чтобы вершина A совместилась с вершиной D, сторона AB – с равной ей стороной DE, а вершины C и F оказались по одну сторону от прямой DE.
Так как A = D и B= E, то сторона AC наложится на луч DF, а сторона BC – на луч EF. Поэтому вершина C – общая точка сторон AC и BC – окажется лежащей как на луче DF, так и на луче EF и, следовательно, совместится с общей точкой этих лучей – вершиной F. Значит, совместятся стороны AC и DF, BC и EF.
Итак, треугольники ABC и DEF полностью совместятся, поэтому они равны.

Теорема доказана.

C

A

B

Рис. 8

D

E

F

Доказательство