- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по математике на тему Сочетания
Содержание
- 2. Комбинаторные задачиПерестановки(n элементовn мест)Отличаются порядком элементовРазмещения(n элементовk
- 3. Сколько возможных перестановок можно составить из данных элементов? Соединения, отличающиеся друг от друга порядком элементов
- 4. Сколько возможных размещений по 2 можно составить
- 5. В турнире участвуют пять команд. Сколько вариантов
- 6. Выпишем возможные варианты смешивания красок, учитывая, что
- 7. СочетанияЧисло всех выборов k элементов из n
- 8. Комбинаторные задачиПерестановки(n элементовn мест)Отличаются порядком элементовРазмещения(n элементовk
- 9. Сколько возможных сочетаний по 2 можно составить
- 10. ЛПосчитайте, сколько возможных сочетаний по 3 можно составить из данных предметовСамостоятельно
- 11. Решение задач№768 В классе 7 человек
- 12. № 770 Учащимся дали список из 10
- 13. Домашнее задание№769, 771
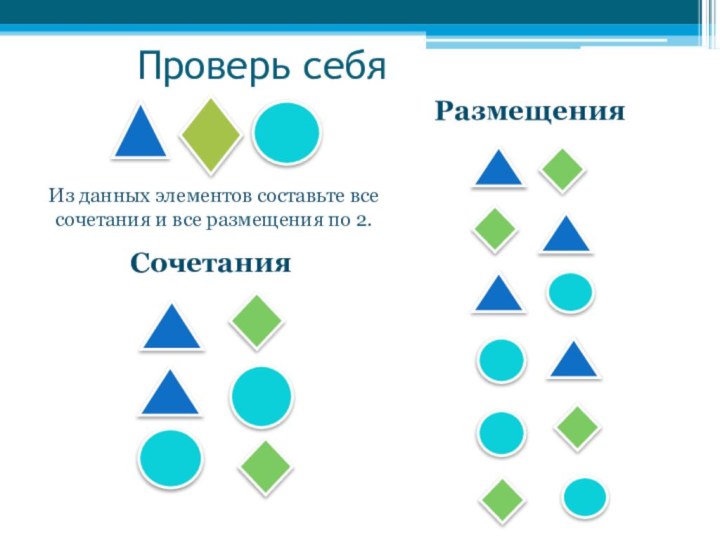
- 14. РазмещенияСочетанияИз данных элементов составьте все сочетания и все размещения по 2.Проверь себя
- 15. Скачать презентацию
- 16. Похожие презентации
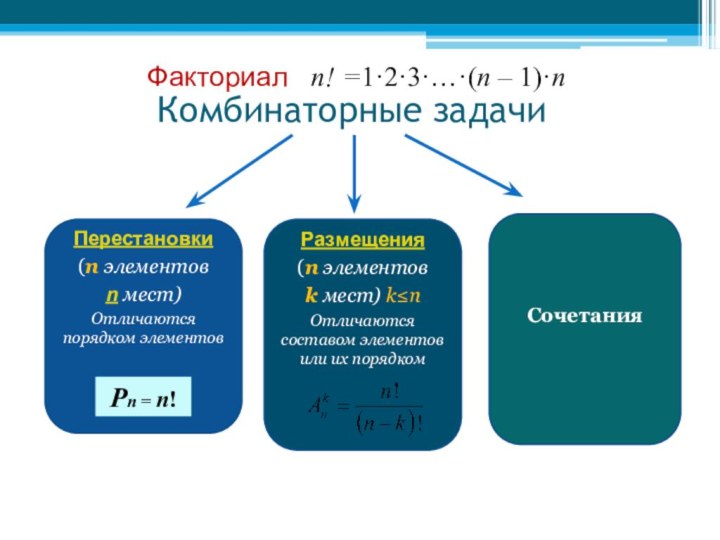
Комбинаторные задачиПерестановки(n элементовn мест)Отличаются порядком элементовРазмещения(n элементовk мест) k≤пОтличаются составом элементов или их порядкомСочетанияРn = n!Факториал n! =1·2·3·…·(n – 1)·n












Слайд 2
Комбинаторные задачи
Перестановки
(n элементов
n мест)
Отличаются порядком элементов
Размещения
(n элементов
k мест)
k≤п
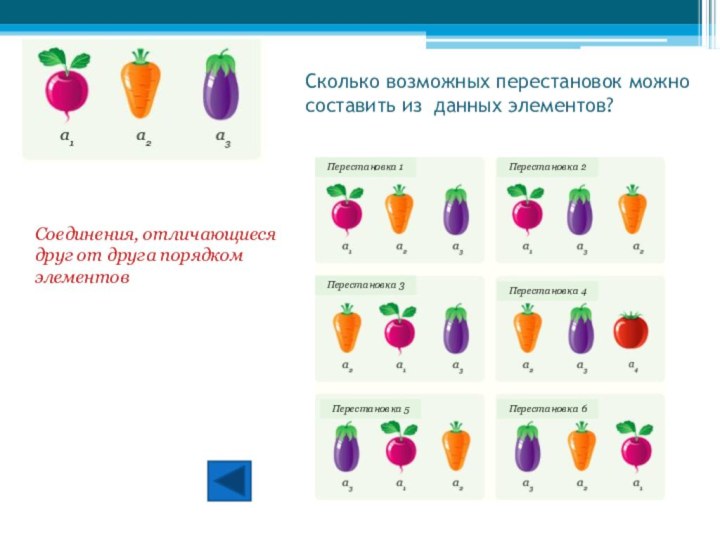
n! =1·2·3·…·(n – 1)·nСлайд 3 Сколько возможных перестановок можно составить из данных элементов?
Соединения, отличающиеся друг от друга порядком элементов
Слайд 4 Сколько возможных размещений по 2 можно составить из
данных элементов?
Соединения, отличающиеся друг от друга составом элементов
или их порядком
Слайд 5
В турнире участвуют пять команд. Сколько вариантов распределения
мест между ними возможно?
Учащиеся 2 класса изучают 9
предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?Сколькими способами можно смешать по три краски из имеющихся пяти?
Определите тип задачи и реши её
Слайд 6 Выпишем возможные варианты смешивания красок, учитывая, что от
порядка расположения красок результат не зависит:
abc, abd, abe, acd,
ace, ade, bcd, bce, bde
Cde
Указаны различные способы смешивания красок, в которых по-разному сочетаются три краски из данных пяти.
Говорят, что составлены все возможные
сочетания из 5 элементов по 3.
Решение
a
b
c
d
e
Слайд 7
Сочетания
Число всех выборов k элементов из n данных
без учёта порядка называют числом сочетаний из n элементов
по k.
Слайд 8
Комбинаторные задачи
Перестановки
(n элементов
n мест)
Отличаются порядком элементов
Размещения
(n элементов
k мест)
k≤п
Отличаются составом элементов или их порядком
Сочетания
(n элементов
k мест) k≤п
Отличаются
составом элементовРn = n!
Слайд 9 Сколько возможных сочетаний по 2 можно составить из
данных элементов?
Соединения, отличающиеся друг от друга составом элементов
Слайд 10
Л
Посчитайте, сколько возможных сочетаний по 3 можно составить
из данных предметов
Самостоятельно
Слайд 11
Решение задач
№768 В классе 7 человек успешно
занимаются математикой. Сколькими способами можно выбрать из них двоих
для участия в математической олимпиадеСлайд 12 № 770 Учащимся дали список из 10 книг
, которые рекомендовано прочитать во время каникул. Сколькими способами
ученик может выбрать из них 6 книг?Решение задач