- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему для организации занятий в рамках математического кружка или факультатива Софизмы и парадоксы
Содержание
- 2. Понятие софизмаСофизм - (от греческого sophisma –
- 3. Формула успешности софизмУспешность софизма определяется следующей формулой:
- 4. Типичные ошибки при решении софизмов Запрещенные действия;
- 5. Понятие парадоксаПарадокс - (от греч. paradoxos –
- 6. Парадоксы отличаются от софизмов тем, что они возникают
- 7. Из истории софизмовВ Древней Греции «софисты» (от
- 8. Из истории парадоксовТак как парадоксы чаще всего
- 9. Великие софистыПротагор из Абдеры, Горгий из Леонтип, Гиппий из Элиды и Продик из Кеоса.
- 10. Люди, открывшие некоторые парадоксыГегель (история), Гемпель (вороны),
- 11. Виды парадоксов и софизмовПарадокс
- 12. Напишем тождество 4:4=5:5. Вынесем из каждой части
- 13. Ошибка сделана при вынесении общих множителей 4
- 14. Скачать презентацию
- 15. Похожие презентации
Понятие софизмаСофизм - (от греческого sophisma – уловка, ухищрение, выдумка, головоломка), умозаключение или рассуждение, обосновывающее какую-нибудь заведомую нелепость, абсурд или парадоксальное утверждение, противоречащее общепринятым представлениям, и имеющее изначально заложенную ошибку.













Слайд 3
Формула успешности софизм
Успешность софизма определяется следующей формулой:
a + b + c + d + e
+ f, где (a + с + е) составляет показатель силы диалектика, (b + d + f) есть показатель слабости его жертвы.а - отрицательные качества лица (отсутствие развития способности управлять вниманием).
b - положительные качества лица (способность активно мыслить)
с - аффективный элемент в душе искусного диалектика
d - качества, которые пробуждаются в душе жертвы софиста и омрачают в ней ясность мышления
е - категоричность тона, не допускающего возражения, определённая мимика
f - пассивность слушателя
Слайд 4
Типичные ошибки при решении софизмов
Запрещенные действия;
пренебрежение условиями теорем; формул и правил;
ошибочный
чертеж; опора на ошибочные умозаключения.
Слайд 5
Понятие парадокса
Парадокс - (от греч. paradoxos – неожиданный,
странный) – мнение, рассуждение, резко расходящееся с общепринятыми понятиями,
противоречащее (иногда только на первый взгляд) здравому смыслу; формально-логическое противоречие, которое возникает в содержательной теории множеств и формальной логике при сохранении логической правильности хода рассуждений.Слайд 6 Парадоксы отличаются от софизмов тем, что они возникают не
в результате непреднамеренных и намеренных логических ошибок, а из-за
неясности, неопределенности и даже противоречивости некоторых исходных принципов и понятий той или иной науки или же общепринятых норм, приемов и методов познания в целом. Парадоксы последнего рода были широко известны еще в античном мире.Парадокс – это абсолютная истина, софизм – относительная истина.
Слайд 7
Из истории софизмов
В Древней Греции «софисты» (от греческого
слова sofos, означающего мудрость) – учителя философии, красноречия и
мыслители, задачей которых было научить своих учеников «мыслить, говорить и делать», то есть уметь убедительно защитить любую точку зрения.
Слайд 8
Из истории парадоксов
Так как парадоксы чаще всего открываются,
а не придумываются, сложно рассказать что либо об их
истории. Однако мы можем утверждать, что первыми людьми кто вообще оперировал понятием парадокс были те же философы Древней Греции.
Слайд 10
Люди, открывшие некоторые парадоксы
Гегель (история), Гемпель (вороны), Плутарх
(корабль), Паррондо (игры), Берксон (события), Шрёдингер (кот), Харви (Техас)
Слайд 11
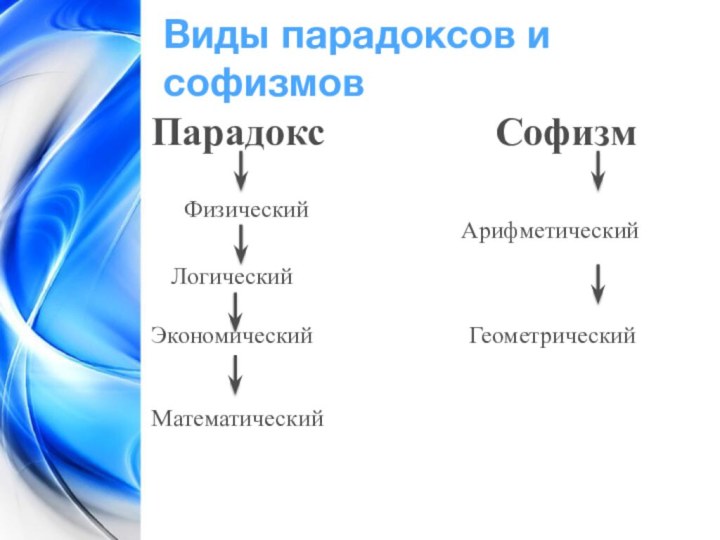
Виды парадоксов и софизмов
Парадокс
Софизм
АрифметическийЛогический
Экономический Геометрический
Математический
Физический
Слайд 12 Напишем тождество 4:4=5:5. Вынесем из каждой части тождества
общие множители за скобки, получаем: 4(1:1)=5(1:1) или (2·2)·(1:1) =
5·(1:1) Так как 1:1=1 , то сократим и получим 2 · 2 = 5Дважды два пять