- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Треугольники в жизни человека
Содержание
- 2. СОДЕРЖАНИЕ1.Что такое треугольник?2.Типы треугольников.3.Признаки равенства треугольников.4.Окружности.5.Ресурсы.
- 3. Что такое треугольник?Треуго́льник — это геометрическая фигура,
- 5. Типы треугольников.По величине углов:Если все углы треугольника
- 6. Признаки равенства треугольников 1. Если сторона
- 7. Определения, связанные с треугольникомМедианой треугольника, проведённой из
- 9. Окружности.Вписанная окружность — окружность, касающаяся всех трёх
- 11. Скачать презентацию
- 12. Похожие презентации









Слайд 2
СОДЕРЖАНИЕ
1.Что такое треугольник?
2.Типы треугольников.
3.Признаки равенства треугольников.
4.Окружности.
5.Ресурсы.
Слайд 5
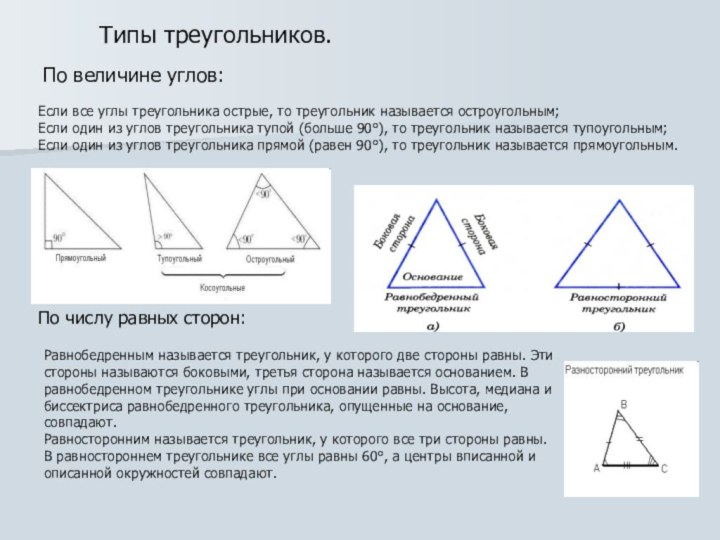
Типы треугольников.
По величине углов:
Если все углы треугольника острые,
то треугольник называется остроугольным;
Если один из углов треугольника тупой
(больше 90°), то треугольник называется тупоугольным;Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным.
По числу равных сторон:
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедренном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
Слайд 6
Признаки равенства треугольников
1. Если сторона и
два прилежащих к ней угла одного треугольника соответственно равны
стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.2.Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
3.Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
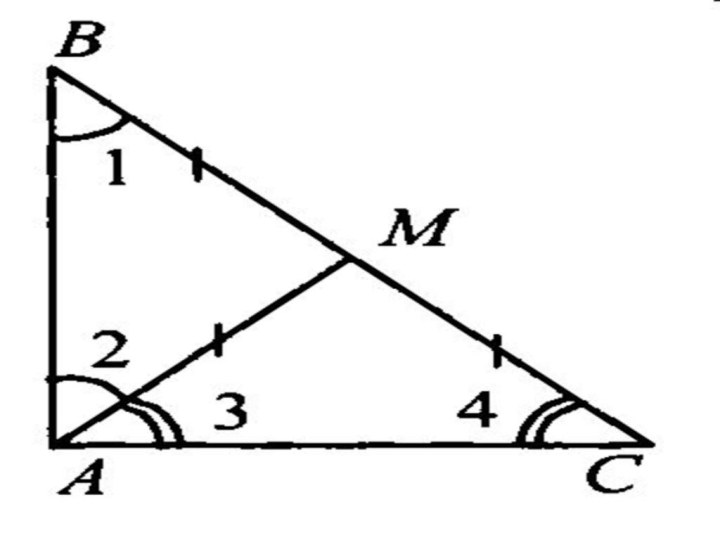
Слайд 7
Определения, связанные с треугольником
Медианой треугольника, проведённой из данной
вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей
стороны (основанием медианы). Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центром тяжести треугольника. Треугольник с вершинами в серединах называется срединным треугольником.Высотой треугольника, проведённой из данной вершины, называется перпендикуляр, опущенный из этой вершины на противоположную сторону или её продолжение. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника. Треугольник с вершинами в основаниях высот называется ортотреугольником.
Биссектрисой треугольника, проведённой из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.
Средней линией треугольника называют отрезок, соединяющий середины двух сторон этого треугольника.
Серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.
Слайд 9
Окружности.
Вписанная окружность — окружность, касающаяся всех трёх сторон
треугольника. Она единственна. Центр вписанной окружности называется инцентром.
Описанная окружность
— окружность, проходящая через все три вершины треугольника. Описанная окружность также единственна.Вневписанная окружность — окружность, касающаяся одной стороны треугольника и продолжения двух других сторон. Таких окружностей в треугольнике три. Их радикальный центр — центр вписанной окружности срединного треугольника, называемый точкой Шпикера.