- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Решение неравенств с помощью квадратичной функции.
Содержание
- 2. Цель урока:
- 3. Разминка ( решение линейных неравенств; алгоритм
- 4. Самопроверка: 1) 3х>9; х>3; Ответ:ХЄ(3; +∞). 2) 8х
- 5. 4) 6х-15≥x+20;
- 8. Свойства функции:Д(f); Е(f);Возрастание, убывание функции;Промежутки знакопостоянства (у>0; у
- 9. Решение квадратичного неравенства с помощью графика кв.
- 10. Вопрос? Скажите как выглядит формула графика квадратичной
- 12. 4 х²+4х+1>0; а) а>0; ветви вверх; б)
- 13. а) 4х²+4х+1≥ 0; Ответ: б)
- 14. - х²+х-1
- 15. Итак, для решения квадратной функции нужно:определить направление
- 16. Закрепление. 1) №665; стр.181. 2) а) х²-6х+9>0; б) 2х²+7х-40;
- 17. проверочная работа.
- 18. Скачать презентацию
- 19. Похожие презентации
Цель урока: 1) Научиться решать квадратные неравенства с помощью графиков функций. 2)Развитие умений и навыков при решений кв.



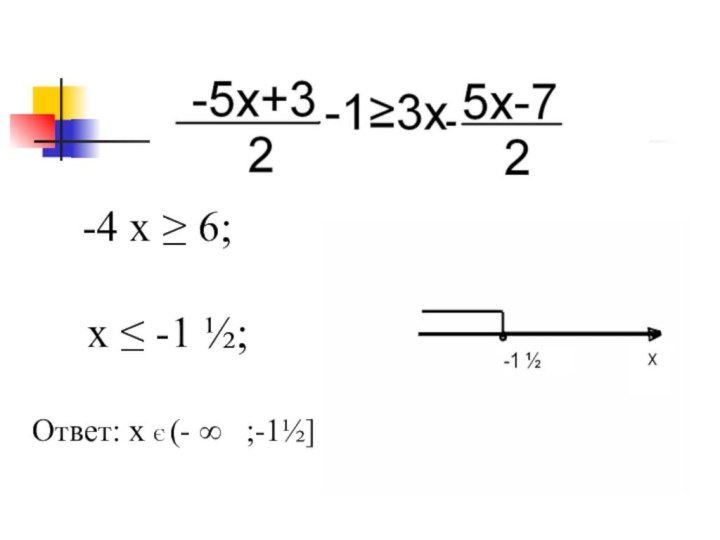







Слайд 3 Разминка ( решение линейных неравенств; алгоритм построения
графика квадратичной функции и её свойства).
Изучение нового материала (
алгоритм решения квадратичного неравенства).Закрепление ( решение упражнений).
Домашнее задание.
План урока:
Слайд 4
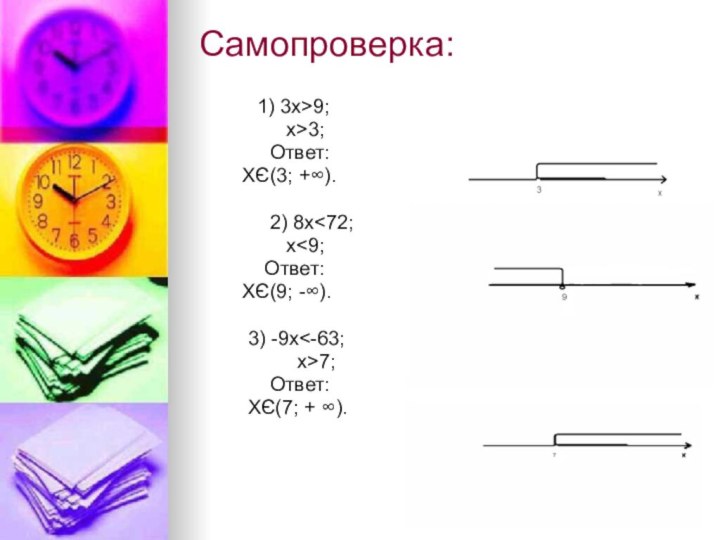
Самопроверка:
1) 3х>9;
х>3;
Ответ:
ХЄ(3; +∞).
2) 8х
x<9;Ответ:
ХЄ(9; -∞).
3) -9х<-63;
x>7;
Ответ:
ХЄ(7; + ∞).
Слайд 5
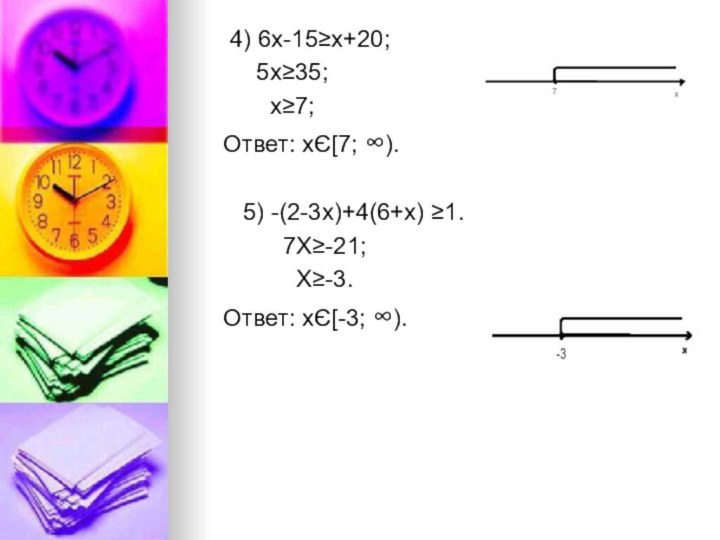
4) 6х-15≥x+20;
5x≥35;
x≥7;
Ответ: хЄ[7; ∞).5) -(2-3x)+4(6+x) ≥1.
7X≥-21;
X≥-3.
Ответ: хЄ[-3; ∞).
Слайд 7
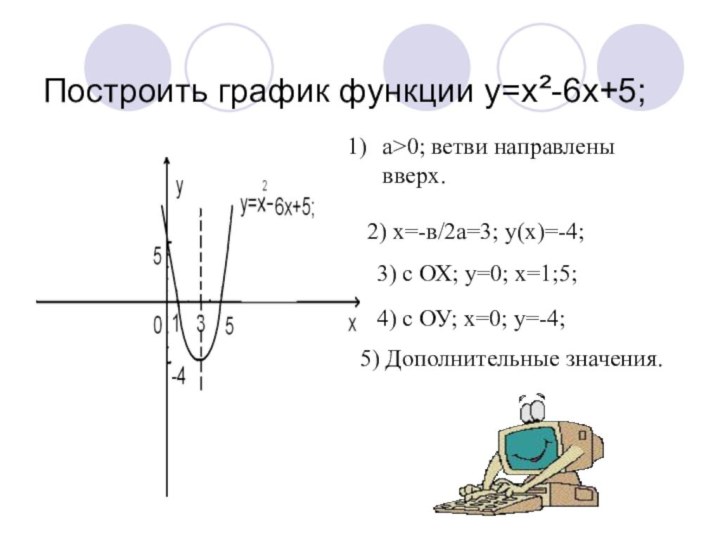
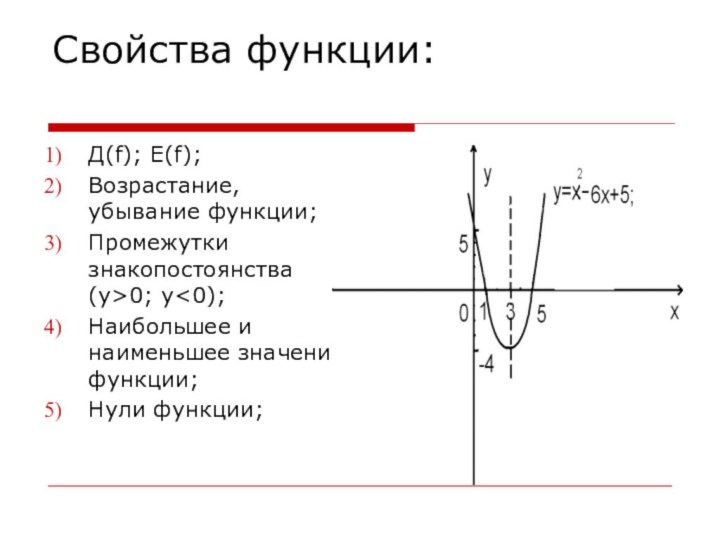
Построить график функции y=x²-6x+5;
а>0; ветви направлены вверх.
2) х=-в/2а=3; у(х)=-4;
3) с ОХ; у=0; х=1;5;
4) с ОУ; х=0; у=-4;
5) Дополнительные значения.
Слайд 8
Свойства функции:
Д(f); Е(f);
Возрастание, убывание функции;
Промежутки знакопостоянства (у>0; у
и наименьшее значение функции;
Нули функции;
Слайд 9
Решение квадратичного неравенства с помощью графика кв. функции.
Методы
решения: с помощью разложения на множители; графический способ; метод
интервалов.Решение квадратного неравенства сводится к отысканию нулей квадратичной функции промежутков, на которых квадратичная функция принимает положительные и отрицательные значения.
Слайд 11
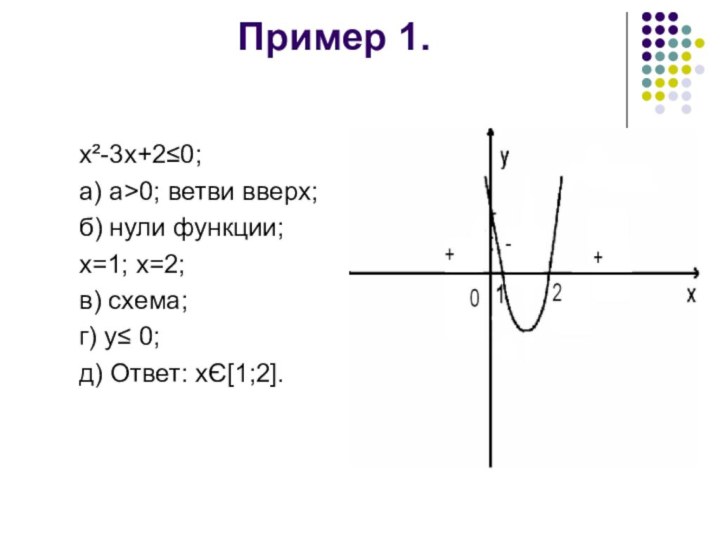
Пример 1.
х²-3х+2≤0;
а) а>0; ветви вверх;б) нули функции;
х=1; х=2;
в) схема;
г) у≤ 0;
д) Ответ: хЄ[1;2].
Слайд 12
4 х²+4х+1>0;
а) а>0; ветви вверх;
б) нули
функции;
х = -½;
в) схема;
г) у>0;
д)) Ответ: R / х = -½;Пример 2.
Слайд 13
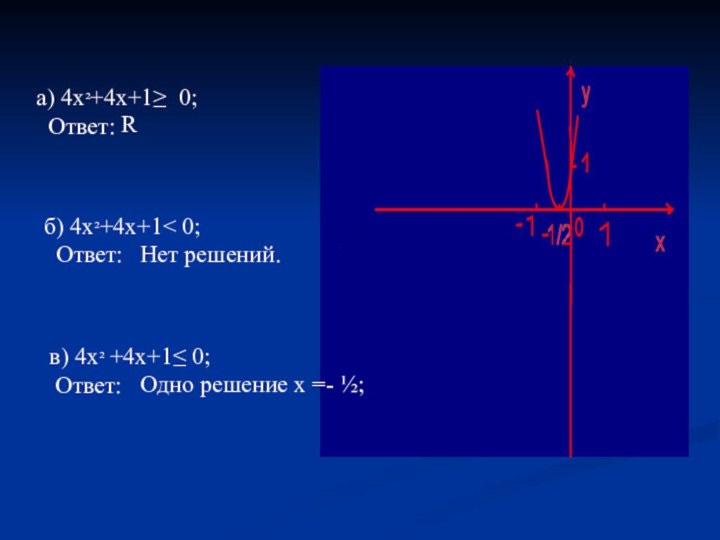
а) 4х²+4х+1≥ 0;
Ответ:
б) 4х²+4х+1
0;
Ответ:
Нет решений.
R
в)
4х² +4х+1≤ 0;Ответ:
Одно решение х =- ½;
Слайд 14
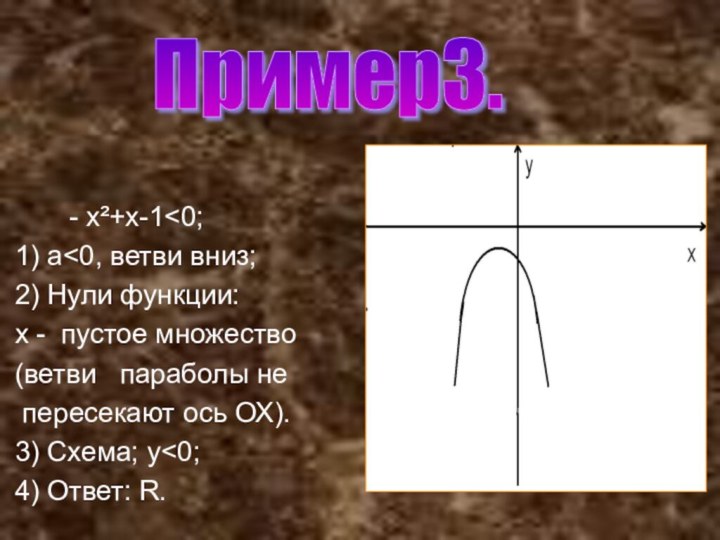
-
х²+х-1
х - пустое множество
(ветви параболы не
пересекают ось ОХ).
3) Схема; у<0;
4) Ответ: R.
Пример3.
Слайд 15
Итак, для решения квадратной функции нужно:
определить направление ветвей
параболы по знаку первого коэффициента квадратичной функции;
Найти действительные корни
соответствующего квадратного уравнения или установить, что их нет;Построить эскиз графика квадратичной функции, используя точки пересечения (или касания) с осью ОХ, если они есть;
По графику определить промежутки, на которых функция принимает нужные значения.





























